“10大排序算法” 总结

最新推荐文章于 2025-07-19 11:40:06 发布
最新推荐文章于 2025-07-19 11:40:06 发布
阅读量315 收藏 6
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 查找排序 文章标签： 查找排序 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/wangqianqianya/article/details/79845100
本文详细介绍了排序算法的不同梯队，包括冒泡排序、鸡尾酒排序、选择排序、插入排序等时间复杂度为O(n^2)的第一梯队算法；快速排序、归并排序、希尔排序、堆排序等时间复杂度为O(nlogn)的第二梯队算法；以及计数排序、桶排序、基数排序等线性时间排序算法。

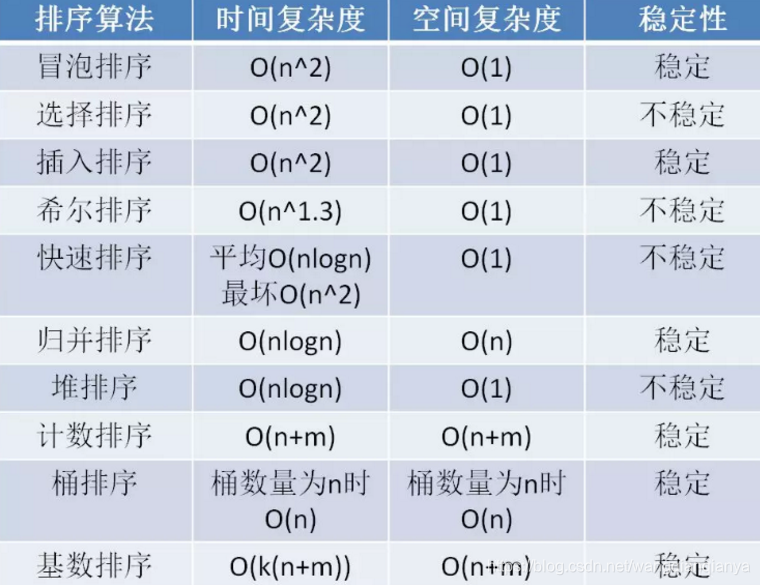
排序算法

第一梯队：时间：O(n^2) 空间:O(1)

冒泡排序【Bubble Sort】

  • 每轮通过依次比较相邻元素，将【最大的元素移至右方】。优化：
  • 不用重复n轮，当某一轮没有一次交换操作时可以跳出循环，排序完成。
  • 每轮不一定要一直比较到第n-1-i个元素，我们可以记录下上一轮进行交换的最后一个元素位置pos，则说明该元素之后的元素都已经排序好了，则该轮只需比较到pos-1即可。
#include<bits/stdc++.h>
#define far(i,t,n) for(int i=t;i<n;++i)
#define pb(a) push_back(a)
#define lowbit(x) x&(-x)
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
int inf=0x3f3f3f3f;
int mod=1e9+7;
const int maxn=1050;

int a[maxn];

void bubbleSort(int a[],int n)
{
    int rightBound=n-2;
    far(i,0,n)
    {
        bool isSwap=0;
        int swapIdx=-1;
        for(int j=0;j<=rightBound;++j)
        {
            if(a[j]>a[j+1])
            {
                isSwap=1;
                swapIdx=j;
                int temp=a[j+1];
                a[j+1]=a[j];
                a[j]=temp;
            }
        }
        if(isSwap==0)
            break;
        rightBound=swapIdx-1;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n)
    {
        far(i,0,n)
            cin>>a[i];
        bubbleSort(a,n);
        far(i,0,n)
            cout<<a[i]<<" ";
        cout<<endl;
    }
}
/*
8
5 8 6 3 9 2 1 7
8
3 4 2 1 5 6 7 8
*/

 鸡尾酒排序

  • 鸡尾酒排序是冒泡排序的一种改进方法：不是每轮都从左开始比较，而是轮流，一轮从左开始比，一轮从右开始比，为什么要这样呢？
  • 我们来看这个例子：2 3 4 5 6 7 8 1 .可以看出前面7个数字已经排好了。按照冒泡排序：第一轮从左到右比较了7次后只交换了8 1 得 2 3 4 5 6 7 1 8,第二轮从左到右比较了6次后只交换了7 1 得 2 3 4 5 6 1 7 8... 我们发现前面的元素重复比较了多次且未交换，就是无意义的比较。按鸡尾酒排序：第一轮从左到右比较了7次后只交换了8 1 得 2 3 4 5 6 7 1 8第二轮从右往左：8已经有序忽略，之后一次交换7 1 、6 1...得 1 2 3 4 5 6 7 8，数组两轮就排序好了。
  • 鸡尾酒排序通过左右交替，可将最大最小的值一次优先排好序，按冒泡排序的优化方法可在左右都记录一个边界值，这样在某些情况下会大大缩小遍历范围。不过代码量增大一倍。
#include<bits/stdc++.h>
#define far(i,t,n) for(int i=t;i<n;++i)
#define pb(a) push_back(a)
#define lowbit(x) x&(-x)
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
int inf=0x3f3f3f3f;
int mod=1e9+7;
const int maxn=1050;

int a[maxn];

void bubbleSort(int a[],int n)
{
    int rightBound=n-2,leftBound=0;
    int i=0;
    while(i<n)
    {
        bool isSwap=0;
        int swapIdx=-1;
        for(int j=leftBound-1;j<=rightBound;++j)
        {
            if(a[j]>a[j+1])
            {
                isSwap=1;
                swapIdx=j;
                int temp=a[j+1];
                a[j+1]=a[j];
                a[j]=temp;
            }
        }
        if(isSwap==0)
            break;
        rightBound=swapIdx-1;
        ++i;
        if(i==n)
            break;

        isSwap=0;
        swapIdx=n;
        for(int j=rightBound+1;j>=leftBound;--j)
        {
            if(a[j]<a[j-1])
            {
                isSwap=1;
                swapIdx=j;
                int temp=a[j-1];
                a[j-1]=a[j];
                a[j]=temp;
            }
        }
        if(isSwap==0)
            break;
        leftBound=swapIdx+1;
        ++i;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    while(cin>>n)
    {
        far(i,0,n)
            cin>>a[i];
        bubbleSort(a,n);
        far(i,0,n)
            cout<<a[i]<<" ";
        cout<<endl;
    }
}
/*
8
2 3 4 5 6 7 8 1
*/

选择排序

  • n-1轮，每次从[i,n)中选出最小的元素，与第i个元素交换。
  • 选择排序复杂度不受原数组影响。
  • 选择排序比冒泡排序少了很多次交换，那为什么还要使用冒泡排序呢？因为选择排序每次是选择最小的换到前面去，这样可能会破坏数组中值相等元素的位置，即选择排序是不稳定的。如5 8 5 3 6 ,则第一轮第一个5被换到第2个5后面去了。
#include<iostream>
using namespace std;
const int N=10;

template <class T>

void select_sort(T a[],int n)
{
     int i,j,minIdx;
     T temp;
     for(i=0;i<n-1;i++)
     {
         minIdx=i;
         for(j=i+1;j<n;j++)
            if(a[minIdx]>a[j])
                minIdx=j;
         temp=a[i];
         a[i]=a[minIdx];
         a[minIdx]=temp;
     }
}

int main()
{
    int a[N]={20,10,45,54,3,6,78,9,49,61};
    int i;
    select_sort(a,N);
    for(i=0;i<N;i++)
      cout<<a[i]<<" ";
    system("pause");
    return 0;
}

插入排序

  • 插入排序就像打扑克牌时，一次处理一张牌。
  • 每插入一张i牌时，前面的i-1张牌已经排好序，所以只需从i-1开始逆序比较该牌与之前的牌，一旦a[i]>=a[j]了，则将第i张牌插入第j张牌之后。
  • 我们可以每轮记录下a[i]的值为nowVar，则可将a[i]的位置当做空位，一旦比较a[j]>a[i]，则将a[j]覆盖到后一个位置(当前的空位)，减少交换次数。
#include<iostream>
using namespace std;
const int N=10;

template <class T>

void select_sort(T a[],int n)
{
    for(int i=1; i<n; i++)
    {
        int nowVar=a[i];
        int j=i-1;
        for(;j>=0;--j)
        {
            if(a[j]>nowVar)
                a[j+1]=a[j];
            else
                break;
        }
        a[j+1]=nowVar;
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int a[100];
    int n;
    while(cin>>n)
    {
        for(int i=0;i<n;++i)
            cin>>a[i];
        select_sort(a,n);
        for(int i=0;i<n;++i)
            cout<<a[i]<<" ";
        cout<<endl;
    }
}

第二梯队：时间：O(nlogn)/O(n^1.3)

快速排序

  • 冒泡排序的改进。
  • 我们知道冒泡排序时间复杂度为O(n*n)，可知n增大，所需时间会增大很多。所以采用分治法可以优化。
  • 快速排序就是通过将选出一个中心元素pivot，将pivot排到它应该在的位置，即左边的元素都<=它，右边的元素都>=它。之后只要分别对 【pivot】 元素左右两部分分别使用快速排序排好即可。
  • 由快速排序的性质可知快速排序可通过 【递归】实现。
  • 怎么选取pivot呢？一个方法是每次选择数组的【第一个元素作为pivot】。不过极端情况可能会快排思想起不到作用：如4 3 2 1 则使用快排得3 2 1 4 -> 2 1 3 4 ->1 2 3 4,pivot值处于边界。所以最好是每次随机选择一个值作为pivot.
  • 怎么将pivot移到正确位置？ 可以采用【挖坑法】方式：（还有一种指针交换法。）
  1. 指针l,r分别指向数组最左、左右端
  2. 若r指向元素>=pivot,则r--，重复直至<,此时将 【a[r]的值放到 l 】处转到步骤3
  3. 若r指向元素<=pivot,则r--，重复直至>,此时，【a[r]的值放到 l 】，转到步骤2
  4. 重复2，3直至l>=r，此时将pivot值赋给a[l]。
#include<iostream>
using namespace std;
const int N=10;

template <class T>
int findPosition(T a[],int s,int e) //挖坑法
{
    int pivot=a[s];
    int l=s,r=e;
    while(l<r)
    {
        while(l<r&&a[r]>=pivot)
            --r;
        a[l]=a[r];
        while(l<r&&a[l]<=pivot)
            ++l;
        a[r]=a[l];
        if(l<r)
        {
            int tmp=a[r];
            a[r]=a[l];
            a[l]=tmp;
        }
    }
    a[l]=pivot;
    return l;
}

template <class T>
void quickSort(T a[],int s,int e)
{
    if(s>=e)
        return;
    int pos=findPosition(a,s,e);
    quickSort(a,s,pos-1);
    quickSort(a,pos+1,e);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int a[100];
    int n;
    while(cin>>n)
    {
        for(int i=0;i<n;++i)
            cin>>a[i];
        quickSort(a,0,n-1);
        for(int i=0;i<n;++i)
            cout<<a[i]<<" ";
        cout<<endl;
    }
}

上述采用的是递归方法，我们知道函数调用有时间消耗，我们可以用栈来模拟递归，也就是用栈记录下每次调用的参数，对pivot元素的调整不变，这里我们就换成指针交换算法：

#include<bits/stdc++.h>
using namespace std;

template <class T>
int findPosition(T a[],int s,int e) //指针交换法
{
    int pivot=a[s];
    int l=s,r=e;
    while(l<r)
    {
        while(l<r&&a[r]>=pivot)
            --r;
        while(l<r&&a[l]<=pivot)
            ++l;
        if(l<r)
        {
            int tmp=a[r];
            a[r]=a[l];
            a[l]=tmp;
        }
    }
    a[s]=a[l];
    a[l]=pivot;
    return l;
}

template <class T>
void quickSort(T a[],int s,int e)
{
    stack<pair<int,int> >stk; //栈模拟，记录参数
    stk.push({s,e});
    while(!stk.empty())
    {
        int l=stk.top().first,r=stk.top().second;
        stk.pop();
        int pos=findPosition(a,l,r);
        if(l<pos-1)
            stk.push({l,pos-1});
        if(r>pos+1)
            stk.push({pos+1,r});
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int a[100];
    int n;
    while(cin>>n)
    {
        for(int i=0;i<n;++i)
            cin>>a[i];
        quickSort(a,0,n-1);
        for(int i=0;i<n;++i)
            cout<<a[i]<<" ";
        cout<<endl;
    }
}

归并排序

  • 分治思想
  • 从低往上看，归并排序就是先两两进行排序，下一轮再两组两组进行排序，重复。

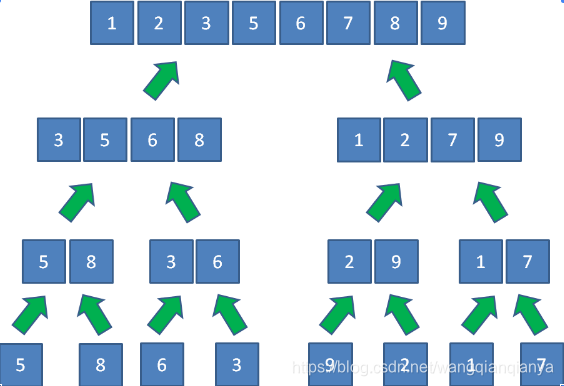
  • 采用递归方式：归并排序分为 用归并排序排好数组左半边、用归并排序排好数组右半边，合并左右半边。
  • 怎么合并左右半边呢？因为左右半边都是排好序的，所以我们只需新开一个数组，长度为两边元素之和，然后用两个指针分别指向两个数组的第一个元素，比较插入新数组，最后再复制回原数组。
  • 归并排序空间复杂度o(n)

 

#include<iostream>
using namespace std;
const int N=100;

template <class T>
void Merge(T a[], int s, int mid, int e)
{
    int n1 = mid-s+1;        //第一个合并数据的长度
    int n2 = e-mid;           //第二个合并数据的长度
    T *L = new T[n1+1];        //申请一个保存第一个数据的空间
    T *R = new T[n2+1];        //申请二个保存第一个数据的空间
    for (int i=0; i<n1; ++i)        //复制第一个数据到临时空间里面
        L[i] = a[s+i];
    L[n1] = INT_MAX;                    //将最后一个数据设置为最大值(哨兵)
    for (int i=0; i<n2; ++i)        //复制第二个数据到临时空间里面
        R[i] = a[mid+i+1];
    R[n2] = INT_MAX;   //将最后一个数据设置为最大值(哨兵)

    n1 =  n2 = 0;
    while(s <= e)
    {
        a[s++] = L[n1] <  R[n2] ? L[n1++] : R[n2++];        //取出当前最小值到指定位置
    }
    delete L;
    delete R;
}

template <class T>
void MergeSort(T a[], int s, int e)
{
    if(s<e)
    {
        int mid=(s+e)/2;
        MergeSort(a,s,mid);
        MergeSort(a,mid+1,e);
        Merge(a,s,mid,e);
    }
}
int main()
{
    int a[N],i,n;
    while(cin>>n)
    {
        for(i=0; i<n; i++)
            cin>>a[i];
        MergeSort(a,0,n-1);
        for(i=0; i<n; i++)
            cout<<a[i]<<" ";
        cout<<endl;
    }
    return 0;
}

希尔排序

  • 插入排序的改进。
  • 我们知道插入排序时间复杂度为O(n*n)，可知n增大，所需时间会增大很多。希尔排序就是通过将数据分组进行插入排序。

堆排序

  • 最大堆：对于每个节点，它的值>=左右节点的值。二叉堆本质是完全二叉树。
  • 用数组模拟二叉堆，左孩子=parent*2+1,右孩子=parent*2+2
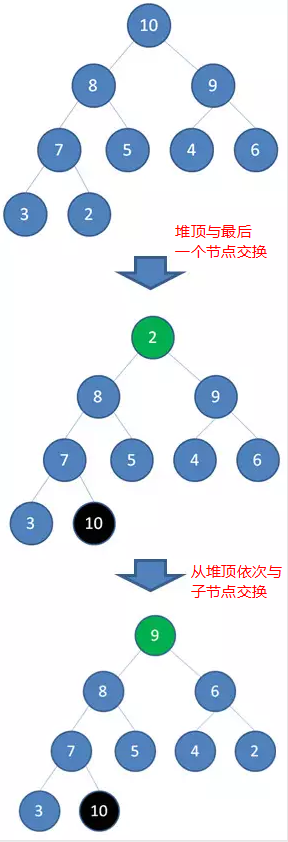
  • 堆的自我调整：父节点与大于它值的最大的子节点交换，直至不再交换为止。由于是向下交换，所以最开始调整为二叉堆时从下往上调整。
  • 步骤：
  1. 将原无序数组调整成最大堆
  2. 每次删除堆顶元素【交换到当前二叉堆的最后一个节点】
  3. 删除完最后一个后数组就被排好序了。

删除堆顶：

#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;

template <class T>
void adjustNode(T a[],int parent,int n)
{
    int child=parent*2+1;
    while(child<n)
    {
        if(child+1<n&&a[child+1]>a[child])
            child++;
        if(a[parent]>a[child])
            break;
        int temp=a[child];
        a[child]=a[parent];
        a[parent]=temp;
        parent=child;
        child=parent*2+1;
    }
}

template <class T>
void heapSort(T a[], int n )
{
    //将无序数组调整成大顶堆
    for(int i=(n-2)/2;i>=0;--i)
        adjustNode(a,i,n);
    //依次删除堆顶
    for(int i=n-1;i>0;--i)
    {
        swap(a[0],a[i]);
        adjustNode(a,0,i);
    }
}

int main()
{
    int i,n;
    int a[100];
    while(cin>>n)
    {
        for(i=0; i<n; i++)
            cin>>a[i];
        heapSort(a,n);
        for(i=0; i<n; i++)
            cout<<a[i]<<" ";
        cout<<endl;
    }
    return 0;
}
/*
8
2 3 4 5 6 7 8 1
*/

 

第三梯队：线性时间排序算法

详情及代码参见：线性时间排序算法：计数、桶、基数排序

计数排序

  • 针对数据【范围相差不大的整数】的排序。
  • 找到数组a最小值Min与最大值Max，相差范围为m。
  • 将数组a的值映射到[0,m-1]范围内，作为数组num的下标，则num[i]表示数组a中数值为i+Min的个数，这样排序后的数组可以通过遍历一遍num数组获得。
  • 如果要实现稳定性，我们可以对num数组求前缀和得到sum数组，则sum[i]表示a中数值为i+Min的数排到了第sum[i]个。这样倒序遍历一遍a,则sum[a[i]]为稳定排序后a[i]的位置（注意这里的位置是从1开始计数！），--sum[a[i]]。
  • 可看出计数排序是稳定排序，时间复杂度为o(m+n),空间复杂度为o(m)

桶排序

  • 针对计数排序无法处理【浮点型数据】设计
  • 建立m个桶，每个桶代表一个浮点范围。则遍历一遍数组，将数组元素放入对应范围的桶，然后对每个桶的元素分别拍排序，可以采用归并排序等，最后按序依次输出每个桶的元素即可。
  • 怎么确定m及桶的范围呢？我们可以另m=n,即建立n个桶，除了最后一桶范围是[Max,Max],前面各桶的区间按比例确定：区间跨度 = （最大值-最小值）/ （桶的数量 - 1）
     

基数排序

  • 针对计数排序不能对【字符串、范围相差很大的数据】排序的缺陷。如11位的电话号码排序，英文名排序等。
  • 对排序元素的每一位分别进行计数排序。
  • 时间复杂度 O(k(n*m)) , k为元素的最大位数
  • 如果元素的位数不一样，可适当补0。
  • 字符串的排序本应从最高位开始比，所以我们应倒着计数排序，因为后一轮会改变前一轮的排序结果。即LSD（低位优先排序）

 

鸡尾酒排序(双端冒泡排序)
You_are_my_dream的博客
01-29 649
#!/usr/bin/python #coding: utf-8 def cocktail_sort(li, num): "鸡尾酒排序，又名：双端冒泡排序" # 减1为了防止越界 num -= 1 i = 0 while i num: # 将最小的数据排到前面，从后往前遍历 j = num while j > i: # j - 1 不会越界，因为while
排序算法之鸡尾酒排序
rd_w_csdn的博客
08-12 1294
title: 鸡尾酒排序 date: 2024-7-30 10:59:43 +0800 categories: 排序算法 tags: 排序 算法 鸡尾酒排序 description: 鸡尾酒排序，也就是定向冒泡排序, 鸡尾酒搅拌排序, 是冒泡排序的一种变形。此算法与冒泡排序的不同处在于排序时是以双向在序列中进行排序。 math: true 鸡尾酒排序 鸡尾酒排序（Cocktail Shaker Sort）是一种双向冒泡排序算法。它通过双向遍历数组，每次在两端交换元素，从而使得大值和小值可以同时移动到
鸡尾酒排序算法详解
qq_35344198的博客
08-07 4561
一、什么是鸡尾酒排序 1.概念 鸡尾酒排序算法又叫快乐小时排序，它基于冒泡排序算法做了一些优化。冒泡排序算法每一轮都是从左到右进行元素比较，进行单向的位置交换，鸡尾酒排序算法则是双向的元素比较和交换。 2.算法原理 这是一个无序数列：2、3、4、5、6、7、8、1，我们要将它按从小到大排序。按照冒泡排序算法的思想，每一轮将最大的元素移到最右边。 第一轮结果 第二轮结果 第三轮结果 第四轮结果 第五轮结果 第六轮结果 第七轮结果 可以看到该序列2到8已经是有序的，但还需进行7轮排序，而鸡尾酒算
鸡尾酒排序
最新发布
weixin_41213299的博客
07-19 24
笔者最近看算法文章的时候，看到一个鸡尾酒排序的算法，是冒泡排序的一种变种。记录一下，每天一个知识点。鸡尾酒排序（Cocktail Sort），又称双向冒泡排序（Bidirectional Bubble Sort）、摇摆排序（Shake Sort），是对传统冒泡排序的一种改进。它在基本思想上与冒泡排序类似，但排序过程是交替地从左到右和从右到左进行的，从而可以更快地将元素移动到正确的位置。
「鸡尾酒排序」不会？每天一遍，排序再见【超详细】
Edison's 小宇宙
12-24 6863
冒泡排序的实现仍然不是最优，有一种排序算法叫做 「鸡尾酒排序」； 鸡尾酒排序是基于冒泡排序的一种升级； 今天这篇文章就是关于 「鸡尾酒排序」 的详细介绍；
七大经典排序算法总结详解
12-29
本文将详细讲解七大经典排序算法，帮助你深入理解它们的工作原理、优缺点以及适用场景。 1. 冒泡排序（Bubble Sort） 冒泡排序是最基础的排序算法之一，通过重复遍历数组，比较相邻元素并交换位置来实现排序。如果...
最经典的8大排序算法总结
10-30
在本篇总结中，将探讨8种经典的排序算法，分别是冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序、二叉树排序和基数排序。 1. 冒泡排序（Bubble Sort）： 冒泡排序是一种简单的排序算法。它重复地遍历要...
排序算法总结.docx
04-29
本文将对数据结构常见的八大排序算法进行详细阐述，包括它们的基本思想、工作原理以及适用场景。 1. 直接插入排序： 直接插入排序是一种简单直观的排序算法，它的工作原理类似于我们平时手动排序扑克牌。首先，假设...
常见排序算法总结.pdf
03-28
【排序算法总结】 排序算法是计算机科学中处理数据排列的重要工具，主要分为稳定排序和非稳定排序、内排序和外排序两大类。稳定排序保证了相同元素在排序后的相对位置不变，而非稳定排序则不作此保证。内排序是指...
java-排序算法总结
02-27
在编程领域，排序算法是计算机科学中的核心概念，特别是在Java这样的高级编程语言中。排序算法是用来组织和优化数据结构的关键工具，它可以帮助我们快速查找、分析和处理大量数据。本篇将深入探讨Java中实现的几种...
java交换排序之鸡尾酒排序实现方法
09-03
主要介绍了java交换排序之鸡尾酒排序实现方法,实例分析了排序的原理与相关的实现技巧,需要的朋友可以参考下
视频动画 | 什么是鸡尾酒排序？
程序员吴师兄的博客
12-16 368
点击蓝色“五分钟学算法”关注我哟加个“星标”，天天中午 12:15，一起学算法来源 | 算法无遗策鸡尾酒排序其实就是冒泡排序的变形，它的时间复杂度和冒泡排序一样，都是O(n^2)，比快速...
算法笔记：鸡尾酒排序算法
qq_40206371的博客
10-26 353
鸡尾酒排序算法是对冒泡排序算法的优化，它的复杂度和稳定性和冒泡排序算法是一致的，时间复杂度为O(N^2)，空间复杂度为O(1)【虽然轮次减少，所以所需时间会比冒泡算法稍微少一些】需要7轮（即使2~8已经排序完成了，但也需要一个一个冒泡到相应的位置去）那么鸡尾酒算法第二轮结束的时候已经排序完成了，比冒泡排序少了很多轮。第二轮，则从右向左进行比较、交换。
排序算法系列之鸡尾酒排序
胡小聪246的博客
07-16 3425
鸡尾酒排序 1 基本原理 1 核心思想：鸡尾酒排序是冒泡排序的一种改进和变型 ，又称“双向冒泡排序”，鸡尾酒排序是从低到高然后从高到低来回排序（选出最大和最小项），比冒泡排序的效率稍微好一点，原因是冒泡排序只从一个方向进行比对(由低到高)，每次循环只移动一个项目。 2 算法分析： 1. 先对数组从左到右进行冒泡排序（升序），则最大的元素去到最右端 ...
【算法分析】排序算法：鸡尾酒排序
hujingshuang
09-26 4494
鸡尾酒排序算法是一种定向的冒泡法排序算法，又叫鸡尾酒搅拌排序、来回排序、涟漪排序等。
【排序算法】鸡尾酒排序的实现与分析
Maggie's Blog
09-07 3712
以升序排序为例： 算法思路 鸡尾酒排序即双向的冒泡排序，是冒泡排序的轻微变形。 它的主要思路是对于一组无规律排放的数字，先找到最大的数字放到最后一位，在反向找到最小的数字放到第一位。然后再找第二大的数字放到倒数第二位，再找第二小的数字放到第二位。以此类推，直到所有数字有序排列。 代码实现 public class CocktailSort
黄海安总结八大排序算法要点
黄海安-八大排序算法总结这一主题所涉及的知识点主要围绕着计算机科学中基础且重要的一部分——数据排序。排序算法是一种对元素序列进行排序的方法，其目的是将一组数据按照一定的顺序排列，常见的顺序包括从小到大...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值