数值的数学表达
我们知道,在硬件中使用二进制补码表示整数,即对于一个 nnn-bits 的整数 XXX,其二进制补码表示为:
[X]补=xn−1xn−2...x0[X]_补=x_{n-1}x_{n-2}...x_{0}[X]补=xn−1xn−2...x0,
其中,xmx_{m}xm 表示补码第 mmm-bit 的值,取值只能为0或1。
我们假设在此文中,对于有符号数,最高位 xn−1x_{n-1}xn−1 为符号位,对于无符号数,没有符号位,即最高位 xn−1x_{n-1}xn−1 为正常数值。
因此,在无符号数的情况下,X=∑i=0n−1xi2iX=\sum_{i=0}^{n-1}x_{i}2^{i}X=∑i=0n−1xi2i,
在有符号数的情况下,X=−xn−12n−1+∑i=0n−2xi2iX=-x_{n-1}2^{n-1}+\sum_{i=0}^{n-2}x_{i}2^{i}X=−xn−12n−1+∑i=0n−2xi2i
乘法的数学表达
在前节的基础上可以进一步推导乘法的数学表达:
- 无符号数 AAA 和无符号数 BBB 相乘:
AB=(∑i=0n−1ai2i)(∑j=0n−1bj2j)=∑i=0n−1∑j=0n−1aibj2i+jAB=(\sum_{i=0}^{n-1}a_{i}2^{i})(\sum_{j=0}^{n-1}b_{j}2^{j})=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_{i}b_{j}2^{i+j}AB=(∑i=0n−1ai2i)(∑j=0n−1bj2j)=∑i=0n−1∑j=0n−1aibj2i+j - 有符号数 AAA 和无符号数 BBB 相乘:
AB=(−an−12n−1+∑i=0n−2ai2i)(∑j=0n−1bj2j)=−an−1∑j=0n−1bj2j+n−1+∑i=0n−2∑j=0n−1aibj2i+jAB=(-a_{n-1}2^{n-1}+\sum_{i=0}^{n-2}a_{i}2^{i})(\sum_{j=0}^{n-1}b_{j}2^{j})=-a_{n-1}\sum_{j=0}^{n-1}b_{j}2^{j+n-1}+\sum_{i=0}^{n-2}\sum_{j=0}^{n-1}a_{i}b_{j}2^{i+j}AB=(−an−12n−1+∑i=0n−2ai2i)(∑j=0n−1bj2j)=−an−1∑j=0n−1bj2j+n−1+∑i=0n−2∑j=0n−1aibj2i+j - 无符号数 AAA 和有符号数 BBB 相乘:
AB=(∑i=0n−1ai2i)(−bn−12n−1+∑j=0n−2bj2j)=−bn−1∑i=0n−1ai2i+n−1+∑i=0n−1∑j=0n−2aibj2i+jAB=(\sum_{i=0}^{n-1}a_{i}2^{i})(-b_{n-1}2^{n-1}+\sum_{j=0}^{n-2}b_{j}2^{j})=-b_{n-1}\sum_{i=0}^{n-1}a_{i}2^{i+n-1}+\sum_{i=0}^{n-1}\sum_{j=0}^{n-2}a_{i}b_{j}2^{i+j}AB=(∑i=0n−1ai2i)(−bn−12n−1+∑j=0n−2bj2j)=−bn−1∑i=0n−1ai2i+n−1+∑i=0n−1∑j=0n−2aibj2i+j - 有符号数 AAA 和有符号数 BBB 相乘:
AB=(−an−12n−1+∑i=0n−2ai2i)(−bn−12n−1+∑j=0n−2bj2j)=an−1bn−122n−2+∑i=0n−2∑j=0n−2aibj2i+j−(an−1∑j=0n−2bj2j+n−1+bn−1∑i=0n−2ai2i+n−1)AB=(-a_{n-1}2^{n-1}+\sum_{i=0}^{n-2}a_{i}2^{i})(-b_{n-1}2^{n-1}+\sum_{j=0}^{n-2}b_{j}2^{j})=a_{n-1}b_{n-1}2^{2n-2}+\sum_{i=0}^{n-2}\sum_{j=0}^{n-2}a_{i}b_{j}2^{i+j}-(a_{n-1}\sum_{j=0}^{n-2}b_{j}2^{j+n-1}+b_{n-1}\sum_{i=0}^{n-2}a_{i}2^{i+n-1})AB=(−an−12n−1+∑i=0n−2ai2i)(−bn−12n−1+∑j=0n−2bj2j)=an−1bn−122n−2+∑i=0n−2∑j=0n−2aibj2i+j−(an−1∑j=0n−2bj2j+n−1+bn−1∑i=0n−2ai2i+n−1)
乘法竖式的计算
以下均以 4-bits 数为示例演示乘法竖式的计算。
无符号数 AAA 和无符号数 BBB 相乘
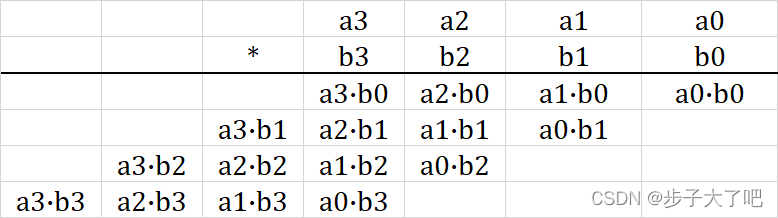
无符号数和无符号数的乘法直接相乘即可,高位补0。
有符号数 AAA 和无符号数 BBB 相乘
在这里为了区分符号位,令 AAA 的符号位为 sa\mathbf{sa}sa。
第一步:根据公式,与符号位相乘的结果需要取负值。
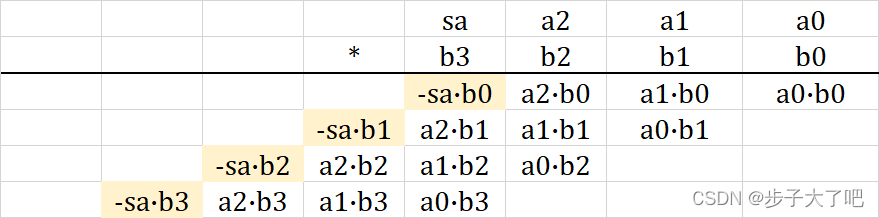
第二步:−sa⋅bx,x=0,1,2,3\mathbf{-sa·bx, x=0,1,2,3}−sa⋅bx,x=0,1,2,3 取值只能为 0或 -1,因此其可以等效为 n′b1...1+1′bsa⋅bx‾\mathbf{n'b1...1+1'b\overline{sa·bx}}n′b1...1+1′bsa⋅bx。

第三步:将多余的 1 提前消去,简化运算。
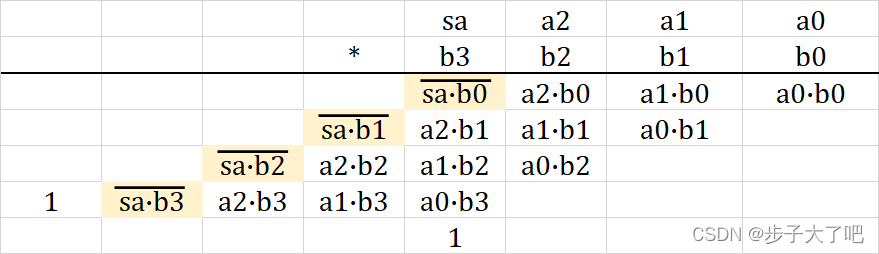
无符号数 AAA 和有符号数 BBB 相乘

与第二种情况相似,可以对这种情况化简如下: 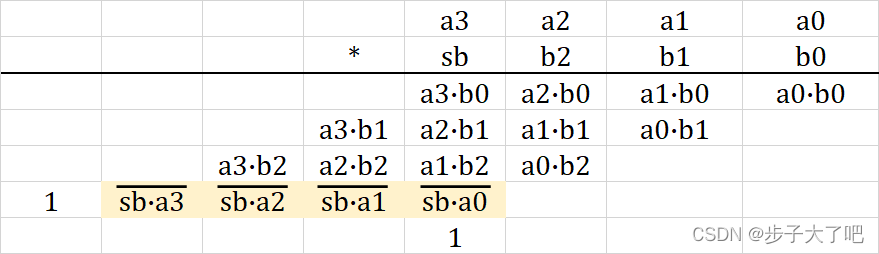
有符号数 AAA 和有符号数 BBB 相乘
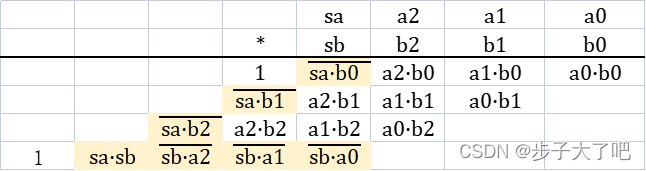
此时根据公式展开后的竖式如下:

对竖式中的负数进行替换:

对替换后公式中的1进行合并:

最后,得到化简后的竖式:
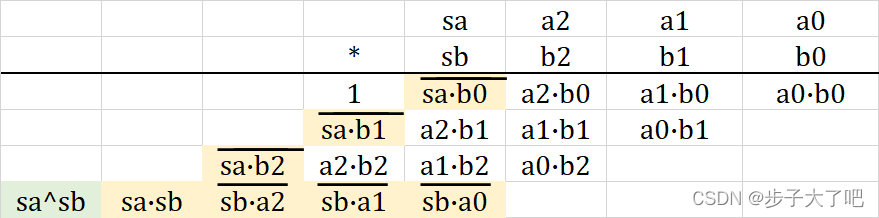
当然,涉及到有符号数的乘法结果的符号位也可以通过乘数的符号位直接求得:





 文章详细介绍了如何用二进制补码表示整数,包括无符号数和有符号数的表示方法。接着,文章阐述了无符号数和有符号数的乘法数学表达式,并提供了乘法竖式的计算过程,特别讨论了不同类型的数相乘时的处理方式,如无符号数与无符号数、有符号数与无符号数以及有符号数与有符号数的乘法。
文章详细介绍了如何用二进制补码表示整数,包括无符号数和有符号数的表示方法。接着,文章阐述了无符号数和有符号数的乘法数学表达式,并提供了乘法竖式的计算过程,特别讨论了不同类型的数相乘时的处理方式,如无符号数与无符号数、有符号数与无符号数以及有符号数与有符号数的乘法。
















 1278
1278

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








