基础算法回顾（二）

递归

递归是调用自己的函数；
递归函数有基线条件和递归条件，决定结束和递归；
递归调用会产生调用栈；
栈有压入和弹出两种操作；
调用链越长，调用栈就会越长，所占用的内存就多；
尾递归可以解决调用栈过长的问题。

快速排序

快速排序使用了分而治之的方法
分而治之：递归式问题解决方法
D&C分而治之的原理：
1.找出简单的基线条件
2.确定如何缩小问题的规模，使其符合基线条件
基线条件是数组为空或只有一个元素。
递归条件是quicksort(less)+[基数值]+quicksort(greater)
工作原理：首先，在数组中找一个基准值，然后，将数组分成小于基准值（less）和大于基准值（greater）的两个数组，再对两个数组分别使用快速排序。
快速排序的性能高度依赖于你选择的基准值。
快速排序最糟糕的情况下时间复杂度是O(n2)。
快速排序平均情况时间复杂度是O(nlogn)。
平均情况是选择的基准值能够将数组分成两个不为空的子数组，此时调用栈的长度为O(logn)。
最糟糕情况下每次选择的基准值分成的两个数组，总有一个为空，此时调用栈的长度为O(n)。

狄克斯特拉算法

狄克斯特拉算法：找出加权图中前往X的最短路径，步骤如下：
(1) 找出最便宜的节点，即可在最短时间内前往的节点。
(2) 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。
(3) 重复这个过程，直到对图中的每个节点都这样做了。
(4) 计算最终路径。
注意：
1.狄克斯特拉算法只适用于有向无环图
2.狄克斯特拉算法背后的关键理念：找出图中最便宜的节点，并确保没有到该节点的更
便宜的路径！
3.不能将狄克斯拉算法用于包含负权边的图，因为该算法基于一个这样的假设：对于一个已经处理的节点，没有前往该节点的更短路径。而这种假设仅在没有负权边的图中才成立。而贝尔曼-福德算法可用于在含有负权边的图中寻找最短路径。
实现：
1.建立三张散列表，图表、开销表、父节点表
图表：存储节点的邻节点及其开销
开销表：存储从起点到达每个节点需要的开销
父节点表：存储每个节点的父节点
2.建立一个数组用于存放已经处理过的节点
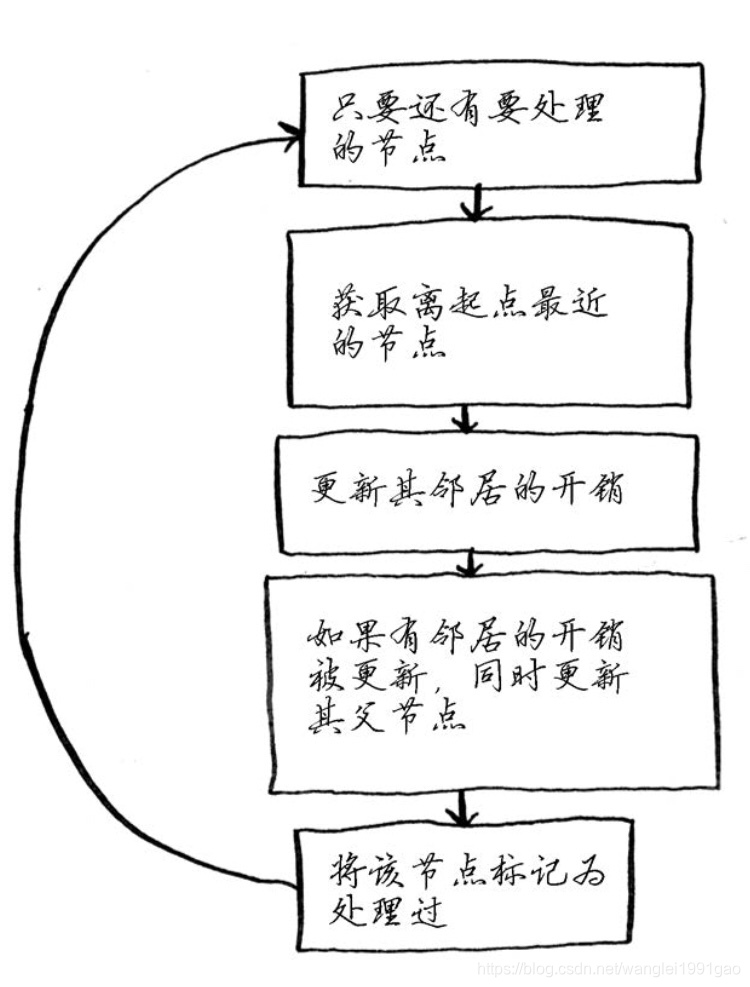
3.执行算法：