基于Siddon算法的CT正投影计算

CT技术在医学诊断、工业无损检测、安检及地质勘测等方面发挥着重要的作用。CT技术的数理基础是Radon变换，在实际的CT系统中，Radon正变换称为投影数据的采集，Radon逆变换称为切片图像重建。CT投影仿真在优化Radon变换的投影成像过程，测试Radon逆变换的CT重建算法等方面具有十分重要的意义。CT投影仿真可以实现任意CT扫描参数设置，同时CT投影仿真为CT重建算法的性能测试提供了重要保障。

本文着重介绍CT正投影常用的Siddon算法，文章全文见https://aapm.onlinelibrary.wiley.com/doi/abs/10.1118/1.595715。

Siddon算法是针对三维空间求射线与体素相交的长度，这里以二维为例，如下图所示。

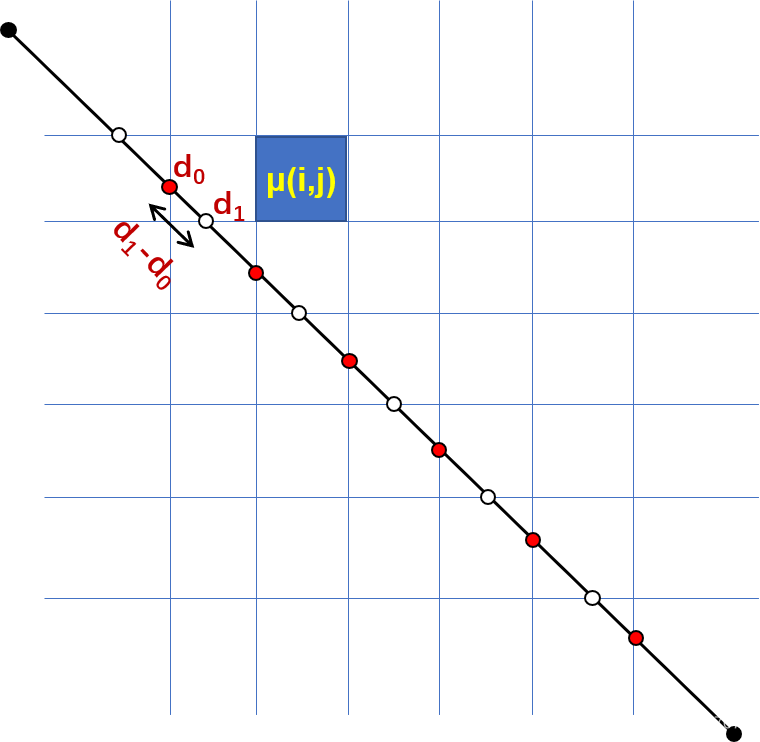
将空间体素离散成X方向、Y方向的一条条网格线(三维就是X、Y和Z方向的网格线)。设射线源的坐标(P1_x,P1_y)，探测器某一单元的坐标为(P2_x,P2_y)，则射线源与该探测器单元的连线就是一条射线。该射线与空间网格的相交情况有两种：（1）该射线穿过待重建的区域（有效射线）；（2）该射线不穿过待重建的区域（无效射线）。无效射线未经过物体区域，即射线未产生衰减，不作讨论。

当射线穿过待重建区域时，会与空间离散的网格线产生一系列交点，如上图所示，红色交点代表射线与X方向网格线的交点，白色交点代表射线与Y方向网格线的交点。该射线上所有点的坐标都可以用x=P1_x + alpha_x*(P2_x - P1_x),y=P1_y + alpha_y*(P2_y - P1_y)来表示，若得到alpha_x和alpha_y，则可以得到点的坐标。

同样，要得到射线与体素相交的长度，则必须得到射线与网格线所有的交点坐标；要得到所有的交点坐标，就必须得到所有交点对应的alpha_x和alpha_y。然后将alpha_x和alpha_y变成一个向量，通过排序，提出重复元素，得到一个向量alpha。射线与体素相交的长度为l(i)=[alpha(i+1) - alpha(i)]*sqrt((p1_x - p2_x)^2 + (p1_y - p2_y)^2)，然后体素的索引也可由向量alpha得到。

详细的程序见https://download.youkuaiyun.com/download/wangkun7673/11970822，该程序是基于等距扇束CT系统进行的投影仿真，采用的是Shepp-logan模型。