RL电路的响应

学完RC电路的响应，又过了一段时间了，想必很多人都忘了RC电路响应的一些内容。我们这次学习RL电路的响应，以此同时，其实也是带大家一起回忆一些之前所学的RC电路的响应的一些知识点。所以，这次的学习，其实也是一次复习哟！#电工基础#

我们先来回顾一些概念。

(1)零输入响应，是指动态电路中无外施激励电源，输入信号为零，仅由动态元件(电感元件或电容元件)的初始储能所产生的响应。

(2)零状态响应，是指电路在零初始状态下(即储能元件的初始能量为零)，仅由外加电源激励所产生的电路响应。

(3)全响应，是指当一个非零初始状态的一阶电路(只有一个动态元件)受到外电源激励时，电路的响应。

动态元件有电容元件和电感元件，我们之前已经学过这两种元件的特性，结合RC电路的响应，举一反三，其实我们可以大概知道RL电路的响应，因为它们都是类似的。

上图43-1所示的RL电路，在开关K动作之前，电感与电源相连，电压与电流已恒定不变，所以电感相当于短路，其两端无压降，电感中有电流I0。在t=0时开关由1合到2，具有初始电流I0的电感L与电阻R相连，构成一个回路。此时电感元件的响应就是RL电路的零输入响应。

可能有的人会疑问，这不是有个电源的存在吗？怎么就是零输入响应了？所以在这里说明一下，RL电路的零输入响应，是指电感元件L初始状态不为零，具有一定的电流流过，例如上图43-1中的I0，当开关K动作，电感元件L就与电源断开连接，与电阻R串联，此时对于电感元件L而言，它就是零输入状态。

如上图43-1右边所示，开关K动作后，电感电流i不能突变，包括大小和方向，所以此时电感对电阻R释放能量，电压方向下正上负。而电阻R消耗能量，电压方向亦为下正上负。

类似于RC电路的零输入响应，根据图43-1右边的电路图，列出RL电路零输入响应的KVL方程，如下图43-2所示，和RC电路一样，式(1)也是一个一阶齐次微分方程。令方程的通解i =Aept，得到电流的表达式(2)。

根据电感电流的初始值求解积分常数A，如下图43-3所示。微分方程的求解过程大家可以不必理会，只要知道方程建立的过程即可。依次求出回路中的电压和电流，并画出它们的曲线。电感的电压除了根据求导公式求得外，还可以直接根据KVL得出。

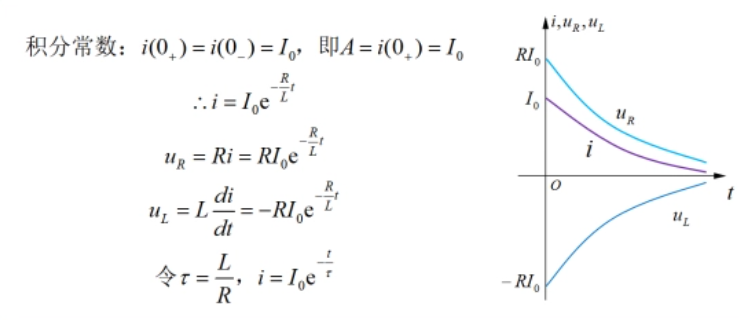
类似于RC电路，在RL电路中，令τ=L/R，称为RL电路的时间常数，则电压、电流表达式中的指数可以用τ表示。

根据表达式或曲线，可以看到，电压、电流都是按同样的指数规律从初始值衰减的，它们衰减的快慢由时间常数L/R决定。

在《电工基础》课程中，曹老师花了较多的时间用日光灯的实例说明了电感产生高压的原理，还有RL直接从直流电源断开瞬间产生高压的弊端与解决措施等，这里我也不展开讲解，大家感兴趣的话可以去看一下课程，那些实例对大家理解RL电路的响应有很大的帮助。

另外，RL电路的零输入响应，以至于接下来要讲的其余两种响应，都可以用我们上一次所学的三要素法求解，曹老师在《电工基础》中，讲解RL电路的零输入响应时就是根据三要素法，这个就更为简单快捷。

我们继续学习RL电路的零状态响应，就利用三要素法来分析。下图43-4为RL电路，开关S在t=0时闭合，电压源的电压施加在电阻R和电感L上。开关闭合时iL(0 )=iL(0-)=0，电路的响应为零输入响应。

根据三要素法，首先要确定三个要素。在RL电路中需要确定的就是电感电流iL的变化规律，确定电感电流的初始值、稳态值和时间常数τ。

由于是零状态响应，电感电流不能突变，可得电流初始值iL(0 )=iL(0-)=0;当电路达到稳定状态时，电感电流不再变化，此时电感元件相当于短路，即iL(∞)=US/R;时间常数τ=L/R，代入图43-4的公式，可以得到电感电流和电压的表达式如图43-5所示。

简单来说，就是开关闭合，电感电流iL不能突变，回路电流为零，电阻上电压uR为零，电源电压全部施加在电感元件上，随着电感电流iL的增大，电感两端的电压uL下降，电阻的分压使得其电压uR增大，最后电路达到稳定状态，电感电流iL不再变化，电感两端的电压uL为零，电源电压全部施加在电阻上，uR=US。

对比RL电路的零输入响应和零状态响应的两种分析方法，可以看到，三要素法比经典法方便很多，但是要懂得三要素法，就一定要理解经典法。我们继续学习RL电路的全响应，依然用三要素法进行分析。

下图43-6的RL电路中，电感电流初始值iL不为零，开关S在t=0时闭合，电阻R2与R3并联，此时流过电感的电流将会发生改变。先后求出三个要素，开关闭合前，电流与电压恒定不变，电感元件元件相当于短路，电流可根据欧姆定律求出；开关闭合后且电路达到新的稳态时，电感依然相当于短路，此时新的电流还是根据欧姆定律求出；时间常数τ的求解，把电压源作短路处理，求出与电感元件相串联的等效电阻，最后代入公式即可得到结果，如图43-6所示。

RL电路的全响应，电感电流是增大还是减小，要视换路前后电路的参数而定，特别是等效电阻的变化，RC电路的全响应也是相同的道理。

对比一下RL电路和RC电路，电路在稳定状态时，电感相当于短路，电容相当于开路，这个有点类似我们之前在学叠加定理时对响应电源的处理，当然，也只是有点类似而言。