LeetCode每日一题(2326. Spiral Matrix IV)

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

Example 1:

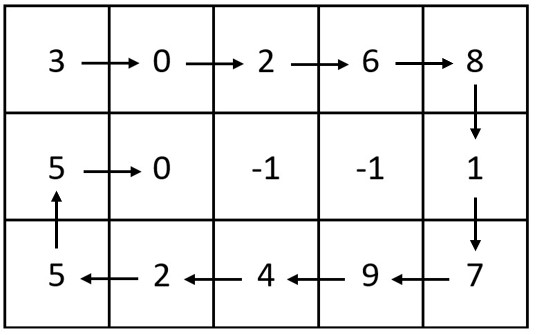
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]

Explanation:
The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.

Example 2:

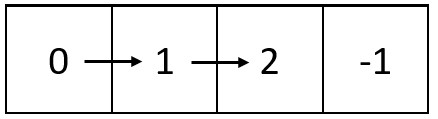
Input: m = 1, n = 4, head = [0,1,2]
Output: [[0,1,2,-1]]

Explanation:
The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.

Constraints:

• 1 <= m, n <= 105
• 1 <= m * n <= 105
• The number of nodes in the list is in the range [1, m * n].
• 0 <= Node.val <= 1000

---

这题包含一个暗示， 就是这个矩阵的格子数量一定是大于链表的节点数量的。 我们首先生成 m * n 的矩阵， 每个格子填充-1， 然后遍历链表同时填充矩阵， 我们从 matrix[0][0]开始， 一开始的方向是向右， 如果遇到矩阵的边界或者已经填充的格子(值不为-1), 则换方向， 方向转换方式为: 右 -> 下 -> 左 -> 上 -> 右

---

impl Solution {
    pub fn spiral_matrix(m: i32, n: i32, mut head: Option<Box<ListNode>>) -> Vec<Vec<i32>> {
        let mut matrix = vec![vec![-1; n as usize]; m as usize];
        let mut row = 0usize;
        let mut col = 0usize;
        let mut dir = "right";
        while let Some(node) = &mut head {
            matrix[row][col] = node.val;
            match dir {
                "right" => {
                    if col == n as usize - 1 || matrix[row][col + 1] != -1 {
                        dir = "down";
                        row += 1;
                    } else {
                        col += 1;
                    }
                }
                "down" => {
                    if row == m as usize - 1 || matrix[row + 1][col] != -1 {
                        dir = "left";
                        col -= 1;
                    } else {
                        row += 1;
                    }
                }
                "left" => {
                    if col == 0 || matrix[row][col - 1] != -1 {
                        dir = "up";
                        row -= 1;
                    } else {
                        col -= 1;
                    }
                }
                _ => {
                    if row == 0 || matrix[row - 1][col] != -1 {
                        dir = "right";
                        col += 1;
                    } else {
                        row -= 1;
                    }
                }
            }
            head = node.next.take();
        }
        matrix
    }
}