LeetCode每日一题(2002. Maximum Product of the Length of Two Palindromic Subsequences)

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return the maximum possible product of the lengths of the two palindromic subsequences.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

Example 1:

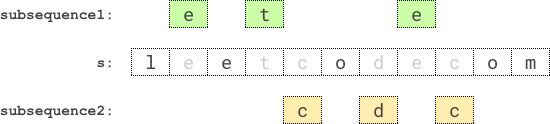
Input: s = “leetcodecom”
Output: 9

Explanation:
An optimal solution is to choose “ete” for the 1st subsequence and “cdc” for the 2nd subsequence. The product of their lengths is: 3 * 3 = 9.

Example 2:

Input: s = “bb”
Output: 1

Explanation:
An optimal solution is to choose “b” (the first character) for the 1st subsequence and “b” (the second character) for the 2nd subsequence.
The product of their lengths is: 1 * 1 = 1.

Example 3:

Input: s = “accbcaxxcxx”
Output: 25

Explanation:
An optimal solution is to choose “accca” for the 1st subsequence and “xxcxx” for the 2nd subsequence.
The product of their lengths is: 5 * 5 = 25.

Constraints:

• 2 <= s.length <= 12
• s consists of lowercase English letters only.

---

我们可以把这个问题转换成从两个字符串中找出的最长回文的问题, 而这两个字符串是从一个字符串拆分出来的。也就是假设我们有两个字符串分别是str1和str2, 还有一个原始字符串str_ori, 那每一个str_ori中的字符一定是被分配到str1或者str2的。到这儿， 我们在看看字符串长度， 不超过 12， 所以我们就可以用 bitset 的方式来把所有str1和str2的可能性遍历出来。然后剩下的事就是从它们当中找最长回文。这里我的思路是一个回文的组成一定是外层对称的一对字母和内层另一个回文， 或者是单个字母。用 dp 的方式来进行查找就可以。但是要注意的是dp[i to j]所代表的是chars[i to j]这个范围内的最长回文， 包括chars[i+1 to j], chars[i to j-1]…

---

use std::collections::HashMap;

impl Solution {
    fn dp<'a>(chars: &'a [char], cache: &mut HashMap<&'a [char], i32>) -> i32 {
        if chars.len() == 0 {
            return 0;
        }
        if chars.len() == 1 {
            return 1;
        }
        let pick = {
            if let Some(i) = chars.iter().rposition(|v| v == &chars[0]) {
                if i == 0 {
                    1
                } else {
                    if let Some(c) = cache.get(&chars[1..i]) {
                        *c + 2
                    } else {
                        Solution::dp(&chars[1..i], cache) + 2
                    }
                }
            } else {
                1
            }
        };
        let ignore = if let Some(c) = cache.get(&chars[1..chars.len()]) {
            *c
        } else {
            Solution::dp(&chars[1..chars.len()], cache)
        };
        let ans = pick.max(ignore);
        cache.insert(chars, ans);
        ans
    }
    pub fn max_product(s: String) -> i32 {
        let chars: Vec<char> = s.chars().collect();
        let mut bitmask = 1;
        let mut ans = 0;
        while bitmask < 2i32.pow(chars.len() as u32) {
            let mut ones = Vec::new();
            let mut zeros = Vec::new();
            let mut mask = bitmask;
            for i in 0..chars.len() {
                if mask & 1 == 1 {
                    ones.push(chars[i]);
                } else {
                    zeros.push(chars[i]);
                }
                mask >>= 1;
            }
            bitmask += 1;
            let one_count = Solution::dp(&ones, &mut HashMap::new());
            let zero_count = Solution::dp(&zeros, &mut HashMap::new());
            ans = ans.max(one_count * zero_count);
        }
        ans
    }
}