概率图模型（PGM）

最新推荐文章于 2025-12-18 17:00:31 发布

原创最新推荐文章于 2025-12-18 17:00:31 发布 · 839 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#算法

人工智能专栏收录该内容

92 篇文章

订阅专栏

概率图模型（Probabilistic Graphical Models，PGM）介绍

1. 基本概念

概率图模型（PGM）是一种通过图形结构来表示变量之间概率关系的模型。它结合了概率论和图论，能够以直观的方式表示变量之间的依赖关系，并通过图形结构进行高效的推理和计算。PGM 主要分为两类：有向图模型（贝叶斯网络）和无向图模型（马尔可夫随机场）。

2. 有向图模型（贝叶斯网络）

定义：贝叶斯网络（Bayesian Network）是一种有向无环图（DAG），其中节点表示随机变量，有向边表示变量之间的条件依赖关系。
表示：每个节点都有一个条件概率分布（CPD），表示在给定其父节点值的情况下该节点的分布。
推理：可以通过贝叶斯定理进行推理，计算变量的后验概率。
应用：贝叶斯网络广泛应用于医疗诊断、故障检测、自然语言处理等领域。

例子

假设我们有一个简单的贝叶斯网络，表示天气（W）、草湿（G）和喷水器（S）之间的关系：

W → S → G
W → G

在这个网络中：

W 表示天气（晴天或下雨）。
S 表示喷水器是否打开。
G 表示草是否湿。

我们可以定义每个节点的条件概率分布：

P(W)：天气的概率分布。
P(S|W)：在给定天气的情况下，喷水器是否打开的概率。
P(G|S, W)：在给定喷水器状态和天气的情况下，草是否湿的概率。

通过这些条件概率分布，我们可以计算出草湿的概率，例如：

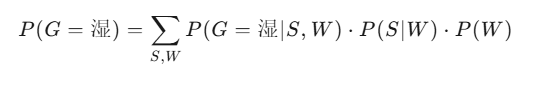
3. 无向图模型（马尔可夫随机场）

定义：马尔可夫随机场（Markov Random Field，MRF）是一种无向图模型，其中节点表示随机变量，无向边表示变量之间的条件独立性。
表示：每个节点的值依赖于其邻居节点的值，但与非邻居节点独立。
推理：可以通过吉布斯分布（Gibbs Distribution）进行推理，计算变量的联合概率。
应用：马尔可夫随机场广泛应用于图像处理、社交网络分析、生物信息学等领域。

例子

假设我们有一个简单的马尔可夫随机场，表示图像中的像素之间的关系：

每个像素的值依赖于其相邻像素的值。

我们可以定义一个吉布斯分布：

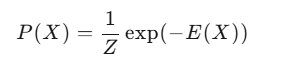
其中 E(X) 是能量函数，表示变量之间的相互作用，Z 是归一化常数。

通过吉布斯分布，我们可以计算出图像中每个像素的值，例如：

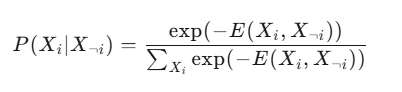
4. 推理算法

精确推理：如变量消除（Variable Elimination）、信念传播（Belief Propagation）等算法，用于计算变量的后验概率。
近似推理：如蒙特卡洛方法（Monte Carlo Methods）、变分推断（Variational Inference）等算法，用于处理复杂的概率图模型。

5. 学习算法

参数学习：通过最大似然估计（MLE）或贝叶斯估计（Bayesian Estimation）等方法，学习概率图模型中的参数。
结构学习：通过搜索算法，如贪心算法、遗传算法等，学习概率图模型的结构。

概率图模型代码示例

以下是一个使用 Python 和 pgmpy 库实现的贝叶斯网络的代码示例：

Python

Copy

from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination

# 定义贝叶斯网络结构
model = BayesianNetwork([('W', 'S'), ('W', 'G'), ('S', 'G')])

# 定义条件概率分布
cpd_w = TabularCPD(variable='W', variable_card=2, values=[[0.7], [0.3]], state_names={'W': ['sunny', 'rain']})
cpd_s = TabularCPD(variable='S', variable_card=2, values=[[0.9, 0.1], [0.1, 0.9]], evidence=['W'], evidence_card=[2], state_names={'W': ['sunny', 'rain'], 'S': ['on', 'off']})
cpd_g = TabularCPD(variable='G', variable_card=2, values=[[0.99, 0.9, 0.8, 0.01], [0.01, 0.1, 0.2, 0.99]], evidence=['W', 'S'], evidence_card=[2, 2], state_names={'W': ['sunny', 'rain'], 'S': ['on', 'off'], 'G': ['dry', 'wet']})

# 将条件概率分布添加到模型中
model.add_cpds(cpd_w, cpd_s, cpd_g)

# 检查模型是否有效
assert model.check_model()

# 推理
inference = VariableElimination(model)
result = inference.query(variables=['G'], evidence={'W': 'sunny', 'S': 'on'})
print(result)

代码说明

定义贝叶斯网络结构：
- 使用 BayesianNetwork 定义网络结构，指定节点之间的有向边。
定义条件概率分布：
- 使用 TabularCPD 定义每个节点的条件概率分布。
- variable_card 表示变量的取值数量。
- values 表示条件概率表。
- evidence 和 evidence_card 表示父节点及其取值数量。
添加条件概率分布：
- 使用 add_cpds 方法将条件概率分布添加到模型中。
检查模型：
- 使用 check_model 方法检查模型是否有效。
推理：
- 使用 VariableElimination 进行推理，计算给定证据下的目标变量的后验概率。