1871：【12NOIP提高组】开车旅行

【题目描述】

小 A 和小 B 决定利用假期外出旅行，他们将想去的城市从 1 到 N 编号，且编号较小的城市在编号较大的城市的西边，已知各个城市的海拔高度互不相同，记城市 i 的海拔高度为Hi，城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值，即d[i,j]=︱Hi-Hj︱。

【输入】

第一行包含一个整数 N，表示城市的数目。

第二行有 N 个整数，每两个整数之间用一个空格隔开，依次表示城市 1 到城市 N 的海拔高度，即 H1，H2，……，Hn，且每个 Hi 都是不同的。

第三行包含一个整数 X0。

第四行为一个整数 M，表示给定 M 组 Si 和 Xi。

接下来的 M 行，每行包含 2 个整数 Si 和 Xi，表示从城市 Si 出发，最多行驶 Xi 公里。

【输出】

输出共 M+1 行。

第一行包含一个整数 S0，表示对于给定的 X0，从编号为 S0 的城市出发，小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小。

接下来的 M 行，每行包含 2 个整数，之间用一个空格隔开，依次表示在给定的 Si 和Xi 下小 A 行驶的里程总数和小 B 行驶的里程总数。

【输入样例】

4
2 3 1 4
3
4
1 3
2 3
3 3
4 3

【输出样例】

1
1 1
2 0
0 0
0 0

【提示】

【输入输出样例 1 说明】

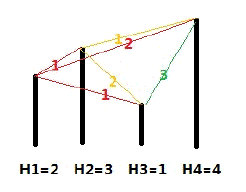
各个城市的海拔高度以及两个城市间的距离如上图所示。

如果从城市 1 出发，可以到达的城市为 2,3,4，这几个城市与城市 1 的距离分别为 1,1,2，但是由于城市 3 的海拔高度低于城市 2，所以我们认为城市 3 离城市 1 最近，城市 2 离城市1 第二近，所以小 A 会走到城市 2。到达城市 2 后，前面可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，所以城市 4 离城市 2 最近，因此小 B 会走到城市 4。到达城

市 4 后，前面已没有可到达的城市，所以旅行结束。

如果从城市 2 出发，可以到达的城市为 3,4，这两个城市与城市 2 的距离分别为 2,1，由于城市 3 离城市 2 第二近，所以小 A 会走到城市 3。到达城市 3 后，前面尚未旅行的城市为4，所以城市 4 离城市 3 最近，但是如果要到达城市 4，则总路程为 2+3=5>3，所以小 B 会直接在城市 3 结束旅行。

如果从城市 3 出发，可以到达的城市为 4，由于没有离城市 3 第二近的城市，因此旅行还未开始就结束了。

如果从城市 4 出发，没有可以到达的城市，因此旅行还未开始就结束了。

【输入输出样例 2】

输入：

10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7

输出：

2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0

【输入输出样例 2 说明】

当 X=7 时，如果从城市 1 出发，则路线为 1 -> 2 -> 3 -> 8 -> 9，小 A 走的距离为 1+2=3，小 B 走的距离为 1+1=2。（在城市 1 时，距离小 A 最近的城市是 2 和 6，但是城市 2 的海拔更高，视为与城市 1 第二近的城市，所以小 A 最终选择城市 2；走到 9 后，小 A 只有城市 10 可以走，没有第 2 选择可以选，所以没法做出选择，结束旅行）

如果从城市 2 出发，则路线为 2 -> 6 -> 7 ，小 A 和小 B 走的距离分别为 2，4。

如果从城市 3 出发，则路线为 3 -> 8 -> 9，小 A 和小 B 走的距离分别为 2，1。

如果从城市 4 出发，则路线为 4 -> 6 -> 7，小 A 和小 B 走的距离分别为 2，4。

如果从城市 5 出发，则路线为 5 -> 7 -> 8 ，小 A 和小 B 走的距离分别为 5，1。

如果从城市 6 出发，则路线为 6 -> 8 -> 9，小 A 和小 B 走的距离分别为 5，1。

如果从城市 7 出发，则路线为 7 -> 9 -> 10，小 A 和小 B 走的距离分别为 2，1。

如果从城市 8 出发，则路线为 8 -> 10，小 A 和小 B 走的距离分别为 2，0。

如果从城市 9 出发，则路线为 9，小 A 和小 B 走的距离分别为 0，0（旅行一开始就结束了）。

如果从城市 10 出发，则路线为 10，小 A 和小 B 走的距离分别为 0，0。

从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小，但是城市 2 的海拔更高，所以输出第一行为 2。

【数据范围】

对于 30%的数据，有 1≤N≤20，1≤M≤201≤N≤20，1≤M≤20；

对于 40%的数据，有 1≤N≤100，1≤M≤1001≤N≤100，1≤M≤100；

对于 50%的数据，有 1≤N≤100，1≤M≤1,0001≤N≤100，1≤M≤1,000；

对于 70%的数据，有 1≤N≤1,000，1≤M≤10,0001≤N≤1,000，1≤M≤10,000；

对于 100%的数据，有 1≤N≤100,000，1≤M≤10,000，−1,000,000,000≤Hi≤1,000,000,000，0≤X0≤1,000,000,000，1≤Si≤N，0≤Xi≤1,000,000,0001≤N≤100,000，1≤M≤10,000，−1,000,000,000≤Hi≤1,000,000,000，0≤X0≤1,000,000,000，1≤Si≤N，0≤Xi≤1,000,000,000，数据保证 HiHi 互不相同。

作者很懒，直接上代码！

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cctype>
#define N 100005
#define ll long long
ll n,h[N],f[N][18],fa[N][18],fb[N][18],pp[N];
struct node{
    ll num,h,pre,nxt;
    bool operator <(const node& rhs)const{return h<rhs.h;}
}li[N];
struct city{
    ll fst,sec;
}p[N];
inline ll readint(){
    char c=getchar();
    bool b=false;
    for(;!isdigit(c);c=getchar())b=c=='-';
    ll d=0;
    for(;isdigit(c);c=getchar())d=(d<<3)+(d<<1)+(c^'0');
    return b?-d:d;
}
inline ll abs(ll a){return a<0?-a:a;}
ll find(ll h){
    ll l=1,r=n;
    while(l<=r){
        ll mid=l+r>>1;
        if(li[mid].h==h)return mid;
        if(li[mid].h<h)l=mid+1;else
        r=mid-1;
    }
}
void query(ll now,ll x,ll& a,ll& b){
    a=b=0;
    for(ll j=17;j>=0;--j){
        if(f[now][j]&&fa[now][j]+fb[now][j]<=x){
            x-=fa[now][j]+fb[now][j];
            a+=fa[now][j];
            b+=fb[now][j];
            now=f[now][j];
        }
    }
    if(p[now].sec&&fa[now][0]<=x)a+=fa[now][0],now=p[now].sec;
}
int main(){
    n=readint();
    for(ll i=1;i<=n;++i)h[i]=readint(),li[i]=(node){i,h[i],0,0};
    std::sort(li+1,li+n+1);
    li[0]=(node){0,-0x3f3f3f3f3f3f3f3f,0,0};
    li[n+1]=(node){0,0x3f3f3f3f3f3f3f3f,n+1,n+1};
    for(ll i=1;i<=n;++i)li[i].pre=i-1,li[i].nxt=i+1;
    memset(fa,-1,sizeof fa);
    memset(p,0,sizeof p);
    memset(f,0,sizeof f);
    memset(pp,0x3f,sizeof pp);
    for(ll i=1;i<=n;++i){
        ll t=find(h[i]);
        ll lh=li[li[t].pre].h,rh=li[li[t].nxt].h;
        if(h[i]-lh>rh-h[i]){
            p[i].fst=li[li[t].nxt].num;
            pp[i]=rh-h[i];
            p[i].sec=li[li[t].pre].num;
            fa[i][0]=lh;
        }else{
            p[i].fst=li[li[t].pre].num;
            pp[i]=h[i]-lh;
            p[i].sec=li[li[t].nxt].num;
            fa[i][0]=rh;
        }
        lh=li[li[li[t].pre].pre].h,rh=li[li[li[t].nxt].nxt].h;
        if(h[i]-lh>rh-h[i]){
            if(rh-h[i]<abs(h[i]-fa[i][0])||rh-h[i]==abs(h[i]-fa[i][0])&&fa[i][0]>rh){
                p[i].sec=li[li[li[t].nxt].nxt].num;
                fa[i][0]=rh;
            }
        }else{
            if(h[i]-lh<abs(h[i]-fa[i][0])||h[i]-lh==abs(h[i]-fa[i][0])&&fa[i][0]>lh){
                p[i].sec=li[li[li[t].pre].pre].num;
                fa[i][0]=lh;
            }
        }
        if(fa[i][0]!=-1)fa[i][0]=abs(h[i]-fa[i][0]);
        li[li[t].nxt].pre=li[t].pre;
        li[li[t].pre].nxt=li[t].nxt;
    }
    for(ll i=1;i<=n;++i)f[i][0]=p[p[i].sec].fst,fb[i][0]=pp[p[i].sec];
    for(ll j=1;j<18;++j)
    for(ll i=1;i<=n;++i)
    if(i+(1<<j)<=n){
        f[i][j]=f[f[i][j-1]][j-1];
        fa[i][j]=fa[i][j-1]+fa[f[i][j-1]][j-1];
        fb[i][j]=fb[i][j-1]+fb[f[i][j-1]][j-1];
    }else break;
    ll x0=readint(),aa=-1,ab=0,ans=0;
    h[0]=0;
    for(ll i=1;i<=n;++i){
        ll a,b;
        query(i,x0,a,b);
        if(!ab&&b)aa=a,ab=b,ans=i;else
        if(!ab&&!b&&h[i]>h[ans])aa=a,ab=b,ans=i;else
        if(aa*b>a*ab||aa*b==a*ab&&h[i]>h[ans]&&aa*b&&a*ab)aa=a,ab=b,ans=i;
    }
    printf("%lld\n",ans);
    for(ll m=readint();m--;){
        ll s=readint(),x=readint(),a,b;
        query(s,x,a,b);
        printf("%lld %lld\n",a,b);
    }
    return 0;
} 

求求给点关注