Description
有T组样例(T<= 10)
每组样例第一行一个数字n(n <= 1e5)
第二行是一个长度为n的字符串(仅包含小写字母)
对于每个样例,给出出现次数最多的字母。
如果有多个字母出现次数最多,请输出最小的那个,例如 'a' < 'b' ,'b' <'e'
Input
有T组样例(T<= 10)
每组样例第一行一个数字n(n <= 1e5)
第二行是一个长度为n的字符串(仅包含小写字母)
Output
对每一个样列,输出一个字母
n=input()
m=int(input())
s1=input()
s1=sorted(s1)#排序,方便以后输出最小的字母
o=int(input())
s2=input()
s2=sorted(s2)
num=1#统计相同的次数
c=[]
d=[]
for i in range(m):
num=1
for j in range(i+1,m):
if s1[i]==s1[j]:
num+=1
c.append(num)
print(s1[c.index(max(c))])#根据索引取值
num=0
for i in range(o):
for j in range(i+1,o):
if s2[i]==s2[j]:
num+=1
d.append(num)
print(s2[d.index(max(d))])
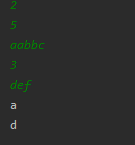




 本文介绍如何使用Python通过排序和计数的方法,快速找出给定字符串中出现次数最多的字母,特别强调了当有多字母出现次数相同时选择最小字母的情况。
本文介绍如何使用Python通过排序和计数的方法,快速找出给定字符串中出现次数最多的字母,特别强调了当有多字母出现次数相同时选择最小字母的情况。

















 4641
4641

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








