2019牛客暑期多校训练营（第一场）

Rank	Solved	A	B	C	D	E	F	G	H	I	J
13/891	6/10	O	O	O	Ø	O	O	Ø	Ø	Ø	O

O: 当场通过

Ø: 赛后通过

.: 尚未通过

A Equivalent Prefixes

solved by chelly

---

chelly’s solution

二分答案，建立前缀的笛卡尔树，判断笛卡尔树是否相同。时间复杂度$O(n\log n)$。

---

viscaria’s solution

考虑前面k个数已经equal，加入第k+1个数对前面的影响，设从后往前第一个比第k+1个数小的数为k_i，那么第k+1个数影响的区间范围就是[i+1,k+1]，如果他们仍要equal，那么2个序列加入的数对区间的影响应该是一模一样的。用单调栈维护一下，可以O(n)的求出。

B Integration

solved by chelly

---

chelly’s solution

比赛时候通过WolframAlpha算积分找规律的……

---

viscaria’s solution
有这么一个公式${\prod }_{i=1}^n\frac{1}{a_i^2+x^2}={\sum }_{i=1}^n\frac{c_i}{a_i^2+x^2}$

并且${\int }_0^{\infty }\frac{c_i}{a_i^2+x^2}=\frac{c_i\pi }{2a_i}$

所以我们想要积分${\int }_0^{\infty }{\prod }_{i=1}^n\frac{1}{a_i^2+x^2}$

那么可以转化为积分${\int }_0^{\infty }{\sum }_{i=1}^n\frac{c_i}{a_i^2+x^2}={\sum }_{i=1}^n\frac{c_i\pi }{2a_i}$

现在的问题就是求$c_i$

${\prod }_{i=1}^n\frac{1}{a_i^2+x^2}={\sum }_{i=1}^n\frac{c_i}{a_i^2+x^2}$

我们可以在等式2边同时乘以${\prod }_i^n{a}_i^2+x^2$，那么就有

$1={\sum }_{i=1}^n{c}_i\ast {\prod }_{j=1}^n(a_j^2+x^2),(j!=i)$

此时我们令$x^2=-a_i^2$，有

$1=c_i\ast {\prod }_{j=1}^n(a_j^2-a_i^2),(j!=i)$，即

$\frac{1}{{\prod }_{j=1}^n(a_j^2-a_i^2)}=c_i,(j!=i)$

这里$n<=1e^3$直接暴力O(n)求$c_i$然后，然后再重复n次求出所有就行了，复杂度$O(n^2)$

C Euclidean Distance

solved by viscaria&chelly

---

chelly’s solution

我们要优化的式子如下：
$$\begin{array}{rl}& \min z=\sum _{i=1}^n(x-\frac{a_i}{m}{)}^2\\ & s.t.\{\begin{array}{ll}\sum _{i=1}^n{x}_i=1,& \\ x_i\ge 0& (j=1,2,3,\cdots ,n).\end{array}\end{array}$$

利用拉格朗日乘子法解决带不等式约束的多元函数极值问题，构造拉格朗日函数：
$$L(x,\mu ,\lambda )=\sum _{i=1}^n(x_i-\frac{a_i}{m})+\mu (\sum _{i=1}^n{x}_i-1)-\sum _{i=1}^n{\lambda }_i{x}_i$$
那么我们要优化的问题就变成了：
$$\begin{array}{rl}& \underset{x}{\min }\underset{\lambda ,\mu }{\max }L(x,\mu ,\lambda )\\ & s.t.{\lambda }_i\ge 0\end{array}$$
由于这里的代价函数和约束函数都是凸函数，所以满足强对偶关系，于是我们要优化的式子就变成了：
$$\begin{array}{rl}& \underset{\lambda ,\mu }{\max }\underset{x}{\min }\sum _{i=1}^n(x_i-\frac{a_i}{m})+\mu (\sum _{i=1}^n{x}_i-1)-\sum _{i=1}^n{\lambda }_i{x}_i\\ & s.t.{\lambda }_i\ge 0\end{array}$$
里面是关于$x$的无约束二次函数，直接可以求得最小值，于是问题变成了优化如下式子：
$$\begin{array}{rl}& \underset{\lambda ,\mu }{\max }\sum _{i=1}^n\frac{-(\mu -\frac{2a_i}{m}-{\lambda }_i{)}^2}{4}+\sum _{i=1}^n(\frac{a_i}{m}{)}^2-\mu \\ & s.t.{\lambda }_i\ge 0\end{array}$$
注意到，当固定某个$\mu$的时候，所有${\lambda }_i$的最优值取值是固定的，这实际上取决于是否满足$\mu \ge \frac{2a_i}{m}$，于是这是关于$\mu$的分段函数，分段求极值即可。注意避免使用分数类，不然会超时。

---

viscaria’s solution

考虑我们这个p能对答案${\sum }_{i=1}^n(\frac{a_i}{m}-p_i{)}^2$造成什么影响

很明显，我们这个是一个n个数的平分和，我们想要他们的和最小。那么我想要每个数都往原点靠

但是不幸的是，p大于0，也就意味着我们只能让这些数减小（减小的总和为p），考虑正数减小，那么和一定减小，考虑负数减小，那么和一定增大。那么我们一定先移正数

我们先移哪些正数呢？先移最大的，因为移动同样的距离，这个数减小得最大

如果我们正数都移到原点了，但是p还没有用完，那我们不得不减小这些负数，我们要考虑怎么移让我们损失最小，也就是加的比较小。那就移距离原点比较近的。

总的来说，我们可以这样计算

1.计算当前点堆能否移动到下一个刚好比他小的点那里里去（因为我们把最大的那个数移到倒数第二大的数的时候，就有2个最大的数了，所以在接下来的操作中，我们应该对这个点堆进行操作，点堆移动的花费应该等于移动的距离乘以点的数量）

2.如果不能，计算最多能移动到哪里，然后break

3.如果可以，更新点堆与花费

最后我们可以得到每个数在哪里，然后计算就可以了

注意答案要求输出分数，其实我们不用维护一个分数类，为什么呢？

因为最后的点的位置一定是一些离散的点加上一个聚在一起的点堆形成的，离散的点就是初始位置，很容易用分数表示，点堆的的话，就等于这堆点的初始位置的和(很容易表示为一个分数)减去p，然后除以点堆数量就行了

D Parity of Tuples

upsolved by chelly

---

chelly’s solution

首先$count(x)=\frac{1}{2^m}{\sum }_{i=1}^n{\prod }_{j=1}^m(1-(-1{)}^{|a_{i,j}\&x|})$
我们可以计算出$count(0..2^k-1)$，然后问题就解决了。
$$\begin{array}{rl}f(x)& =\sum _{i=1}^n\prod _{j=1}^m(1-(-1{)}^{|a_{i,j}\&x|})\\ & =\sum _{i=1}^n\sum _S(-1{)}^{|S|}(-1{)}^{{\sum }_{j\in S}|a_{i,j}\&x|}\\ & =\sum _{i=1}^n\sum _S(-1{)}^{|S|}(-1{)}^{|({\oplus }_{j\in S}{a}_{i,j})\&x|}\\ & =\sum _{V=0}^{2^k-1}(-1{)}^{|V\&x|}(\sum _{i=1}^n\sum _S(-1{)}^{|S|}[({\oplus }_{j\in S}{a}_{i,j})==V])\end{array}$$
注：上面第2行推到第3行是基于这样一个事实：$|a\&x|+|b\&x|\equiv |(a\oplus b)\&x|(mod2)$

于是我们可以先构造$F(V)={\sum }_{i=1}^n{\sum }_S(-1{)}^{|S|}[({\oplus }_{j\in S}{a}_{i,j})==V]$，然后对$F(V)$进行FWT，就可以得到每个$f(x)$了，于是可以计算每个$count(x)$了。
注意计算$F(V)$的时候，直接for循环枚举暴力是$O(nm{2}^m)$的，会TLE，可以利用dfs减少无用的枚举，将复杂度变成$O(n{2}^m)$。
总的时间复杂度是$O(n{2}^m+k{2}^k)$的。

E ABBA

solved by chelly

---

chelly’s solution

---

viscaria’s solution

我们考虑一个合法的序列的前缀，用f(x,y)表示前面有x个A，y个B

我们可以很容易判断出一些前缀是不合法的，哪些前缀呢？

例如在n=1，m=2的情况下，f(2,0),f(3,1)就是一个不合法的前缀，因为前缀至少会给后面留下2个前面的A，而我们只要一个AB

而我们每一个合法的前缀都是由一个更短的合法的前缀转化而来的，例如f(i,j)=f(i,j-1)+f(i-1,j),这代表什么意思呢？

我们在一个合法前缀的最后一个数要么是A要么是B

那么这个合法前缀的数量就是枚举最后一个是A的时候，就转化为f(i-1,j)
枚举最后一个是B的时候，就转化为f(i,j-1)

F Random Point in Triangle

solved by viscaria

---

viscaria’s solution

首先考虑一个三角形，在三角形内随机取一点p，$S\Delta abp$的期望为$\frac{S\Delta abc}{3}$

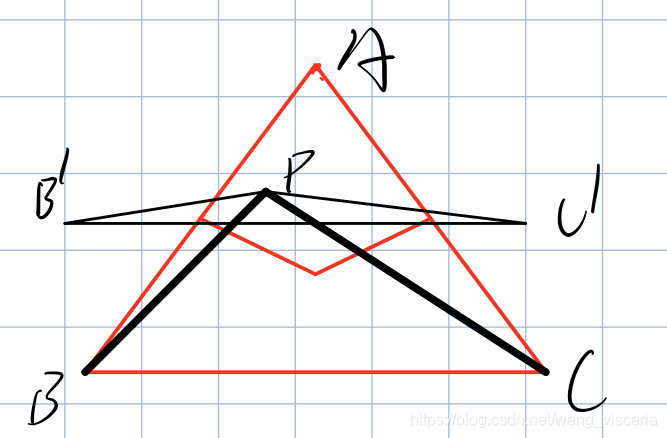
问题就是计算以BC为底的时候，高为h的时候$S\Delta PBC$的期望
设AB中点为D，AC中点为E,重心为O,三角形总面积为S

即$E(S\Delta PBC)=E(S\Delta P{B}^{‘}{C}^{‘}+BC\ast H/2)$
$=E(S\Delta P{B}^{‘}{C}^{‘})+BC\ast H/2$
$=E(S\Delta P{B}^{‘}{C}^{‘})+BC\ast H/2$
$=E(S\Delta PDE)\ast 2+BC\ast H/2$
$=E((S\Delta ADE-S\Delta ODE)/3)\ast 2+BC\ast H/2$（根据开头的引理）
$=((S\Delta ADE-S\Delta ODE)/3)\ast 2+BC\ast H/2$
$=S/6-S/18+S/2$
$=11S/18$

对称性可知，在其他区域期望也一样

G Substrings 2

upsolved by chelly

---

chelly’s solution

H XOR

upsolved by chelly

---

chelly’s solution

很容易想到维护前缀线性基、后缀线性基，然后枚举i，将pre[i-1]和suf[i+1]合并起来，那么i对应的答案就可以求出来了，但这样是$O(64^{2}n)$的，因为线性基合并是$O(64^2)$的，需要进一步优化。
事实上，在我们求pre[i]的过程中，pre[i]与pre[i-1]不同的位置最多只有64个，也就是说处理pre[i]=pre[i-1]的询问i的时候，我们不需要合并线性基，直接拿所有数字的线性基过来用即可。时间复杂度$O(64^3+64n)$。

I Points Division

upsolved by chelly

---

chelly’s solution

一定存在一条xy单调不降的折线把点集划分为AB两个部分，不妨假设折线贴着集合B进行DP。dp[i]表示以i点为最后的最大值，枚举上一个点j，那么需要统计所有$x_j<x_k<x_i,y_k<y_j$的所有点的权值。我们可以拿个线段树维护目前所有点对目前点的dp贡献。可以对y坐标离散后建线段树，tree[y]是目前为止最右边的$x_y=y$的点的贡献。修改就是区间加(加入一个点，要给其左上角所有点加上权值)、单点覆盖(加入一个点，更新$dp[x_y]$)，询问就是区间询问最大值。注意x值相同的点要一起处理。
时间复杂度$O(n\log n)$

J Fraction Comparision

solved by chelly

---

chelly’s solution

__int128签到

Dirty Replay

• A题题意先看错了，WA了一发
• H题卡常，补题的时候T了很多发