UVAlive 7361 Immortal Porpoises（矩阵快速幂）

wang2147483647

于 2016-08-17 22:00:51 发布

阅读量930

点赞数

CC 4.0 BY-SA版权

分类专栏： OJ_UVA 数学_矩阵 ACM 文章标签： UVAlive 矩阵快速幂

本文链接：https://blog.youkuaiyun.com/wang2147483647/article/details/52235119

ACM 同时被 3 个专栏收录

232 篇文章

订阅专栏

OJ_UVA

62 篇文章

订阅专栏

数学_矩阵

1 篇文章

订阅专栏

本文介绍了一种使用矩阵快速幂解决特定类型递推问题的方法。通过定义特定的矩阵，并利用快速幂运算加速递推过程，可以高效求解大规模的递推问题。文中提供了一个具体的示例，展示了如何通过矩阵乘法和快速幂来计算特定数列的第N项。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目地址：https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=5383

思路：

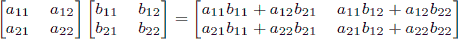
type arr=array[1..2,1..2] of int64;
var
 x,p:int64;
 a,b,c,w:arr;
 cas,i,t:longint;
procedure mul(var a,b,c:arr);
var i,j,k,n:longint;
begin
 n:=2;
 fillchar(w,sizeof(w),0);
 for i:=1 to n do
  for j:=1 to n do
   for k:=1 to n do
    w[i][j]:=(w[i][j]+a[i][k]*b[k][j]) mod p;
 for i:=1 to n do
  for j:=1 to n do
   c[i][j]:=w[i][j];
end;
begin
 readln(cas);
 p:=1000000000;
 for i:=1 to cas do
 begin
   read(t);
   readln(x);
  a[1,1]:=0;a[1,2]:=1;a[2,1]:=0;a[2,2]:=0;
  b[1,1]:=0;b[1,2]:=1;b[2,1]:=1;b[2,2]:=1;
  while (x<>0) do
   begin
    if x mod 2=1 then mul(a,b,a);
    x:=x div 2;
    mul(b,b,b);
   end;
  write(t);
  write(' ');
  writeln(a[1][1]);
 end;
end.