Kruskal算法

1.概述

克鲁斯卡尔算法是求连通网的最小生成树的另一种方法。与普里姆算法不同，它的时间复杂度为O（eloge）（e为网中的边数），所以，适合于求边稀疏的网的最小生成树。

2.算法思想

1.把n个顶点看成看成n棵分离的树（每棵树只有⼀个顶点）

2.每次选取可连接两个分离树中权值最⼩的边把两个分离的树合成⼀个新的树取代原来的两个分离树

3.如果重复n-1步后便得到最⼩⽣成树
 

3.图示

将Kruskal算法应用于如下图表。

解决方案：

边的权重如下：

边	AE	AD	AC	AB	BC	CD	DE
权重	5	10	7	1	3	4	2

根据权重对边进行排序。

边	AB	DE	BC	CD	AE	AC	AD
权重	1	2	3	4	5	7	10

1.选取权重最小的边，连接A-B，将AB从权重表中删除

2.重新从权重表中选取最小的边，判断是否和已有边构成环，没有构成环则连接D-E,将DE从表中删除

 3.继续中权重表中选取权重最小的边，并判断是否构成环，没有构成环则连接B-C,将BC从权重表中删除

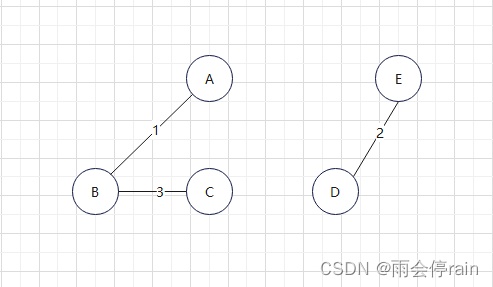
 4.继续重复之前的操作，连接C-D,此时共有五个点，连接了四条边，最小生成树如下

 4.难点

kruskal算法的难点在于连接新的边时，如何判断是否构成环。如何使用代码判断是否生成环。

5.代码实现

/**
 * @author wangli
 * @data 2022/6/15 17:31
 * @Description:
 */
public class KruskalArithmetic {
    private char[] vertexes;//顶点数
    private int[][] matrix;//邻接矩阵
    private int edgeNum; //边的数量
    private static int MAX=Integer.MAX_VALUE;


    public static void main(String[] args){

        char[] vertexs = {'A','B','C','D','E','F','G'};
        int matrix[][] = {
                {0,12,MAX,MAX,MAX,16,14},
                {12,0,10,MAX,MAX,7,MAX},
                {MAX,10,0,3,5,6,MAX},
                {MAX,MAX,3,0,4,MAX,MAX},
                {MAX,MAX,5,4,0,2,8},
                {16,7,6,MAX,2,0,9},
                {14,MAX,MAX,MAX,8,9,0}
        };
        KruskalArithmetic kruskalArithmetic = new KruskalArithmetic(vertexs,matrix);
        kruskalArithmetic.print();
        System.out.println(Arrays.toString(kruskalArithmetic.getEdges()));
        kruskalArithmetic.Kruskal();
    }

    public void Kruskal(){
        //保存最后索引
        int index=0;
        //点对应终点的数组
        int[] ends= new int[edgeNum];
        //最小生成树的结果
        edge[] finalReturn = new edge[edgeNum];
        //将所有的边放入edge[]中
        edge[] edges = getEdges();
        //将边根据权重排序
        bubbleSort(edges);
        //将加入的边判断是否构成回路
        for (int i = 0; i < edges.length; i++) {
            //获取边的起点
            int start = getPosition(edges[i].start);
            //获取边的终点
            int end = getPosition(edges[i].end);
            //获取start这个结点在已有生成树中的终点
            int m = getEnd(ends,start);
            //获取end这个结点在已有生成树中的终点
            int n = getEnd(ends,end);
            //如果两个点的终点不相同，表示满意构成回路
            if(m!=n){
                //将当前边的起点对应终点加入到终点数组中
                ends[m]=n;
                //将此边加入最终最小生成树的数组中
                finalReturn[index++]=edges[i];
            }

        }
        for (int i = 0; i < index; i++) {
            System.out.println(finalReturn[i]);
        }

    }

    /**
     * 初始化构造
     * @param vertexes 顶点数
     * @param matrix 邻接矩阵
     */
    public KruskalArithmetic(char[] vertexes, int[][] matrix) {
        this.vertexes = vertexes;
        this.matrix = matrix;
        for (int i = 0; i < vertexes.length; i++) {
            for (int j = i+1; j < vertexes.length; j++) {
                edgeNum++;
            }
        }
    }
    /**
     * 打印邻接矩阵
     */
    public void print(){
        for (int i = 0; i < vertexes.length; i++) {
            for (int j = 0; j < vertexes.length; j++) {
                System.out.printf("%15d" , matrix[i][j]);
            }
            System.out.println();
        }
    }

    /**
     * 获取当前顶点在vertexes位置
     * @param ch 传入的顶点
     * @return 返回顶点的位置 当为-1表示无此点
     */
    private int getPosition(char ch) {
        for (int i = 0; i < vertexes.length; i++)
            if (vertexes[i] == ch)
                return i;
        return -1;
    }


    /**
     * 创建一个表示边的类
     */
    static class edge{
        public char start;//边的起点
        public char end;//边的终点
        public int weight;//边的权重

        @Override
        public String toString() {
            return "edge{" +
                    "start=" + start +
                    ", end=" + end +
                    ", weight=" + weight +
                    '}';
        }

        public edge(char start, char end, int weight) {
            this.start = start;
            this.end = end;
            this.weight = weight;
        }
    }

    /**
     * 将所有的边放入edge[]中
     * @return edges
     */
    public edge[] getEdges(){
        int index = 0;
        edge[] edges = new edge[edgeNum];
        for(int i = 0; i < vertexes.length;i++) {
            for(int j = i+1;j < vertexes.length;j++)
                if(matrix[i][j]!= MAX )
                    edges[index++] = new edge(vertexes[i],vertexes[j],matrix[i][j]);
        }
        return edges;
    }

    /**
     * 使用冒泡排序对边进行排序
     * @param edges 边的对象数组
     */
    public void bubbleSort(edge[] edges){
        for (int i = 0; i < edges.length-1; i++) {
            for (int j = 0; j < edges.length-1; j++) {
                if (edges[j].weight>edges[i].weight){
                    edge temp =edges[j];
                    edges[j]=edges[i];
                    edges[i]=temp;
                }
            }
        }
    }
    public int getEnd(int ends[],int i){
        while (ends[i]!=0){
            i=ends[i];
        }
        return i;
    }

}

6.返回值