完全二叉树:叶子结点只能出现在最下层和次下层,并且最下层的叶子结点集中在树的左部。没有左叶子结点就一定没有右叶子结点。并且完全二叉树度为1的节点数量要么是0个,要么是1个。

二叉树的总出度=n0+n1+n2。并且n0=n2+1。
二叉树有三种遍历方式:
前序遍历:根-左-右

中序遍历:左-根-右

后序遍历:左-右-根

遍历的算法有两种,一种是递归实现,另一种是非递归,用栈的入栈出栈思想实现。
以中序遍历为例,递归实现:
void InOrderTraverse(BiTree t)
{
if(t != NULL)
{
InOrderTraverse(t->lchild);
printf("%c ", t->data);
InOrderTraverse(t->rchild);
}
}
非递归实现:
int NoInOrderTraverse(BiTree t)
{
SqStack s;
InitStack(&s);
BiTree tmp = t;
if(tmp == NULL)
{
fprintf(stderr, "the tree is null.\n");
return ERROR;
}
while(tmp != NULL || (IsEmpty(&s) != 1))
{
while(tmp != NULL)
{
Push(&s, tmp);
tmp = tmp->lchild;
}
if(IsEmpty(&s) != 1)
{
Pop(&s, &tmp);
printf("%c ", tmp->data);
tmp = tmp->rchild;
}
}
return OK;
}
创建一个二叉树也可以用递归来实现:
BiTree CreateTree(BiTree t)
{
char ch;
scanf("%c", &ch);
if(ch == '#')
{
t = NULL;
}
else
{
t = (BitNode *)malloc(sizeof(BitNode));
if(t == NULL)
{
fprintf(stderr, "malloc() error in CreateTree.\n");
return;
}
t->data = ch; //生成根结点
t->lchild = CreateTree(t->lchild); //构造左子树
t->rchild = CreateTree(t->rchild); //构造右子树
}
return t;
}
二叉查找树:一个结点的左子树结点保存的值小于这个结点保存的值,它的右子树结点保存的值大于。
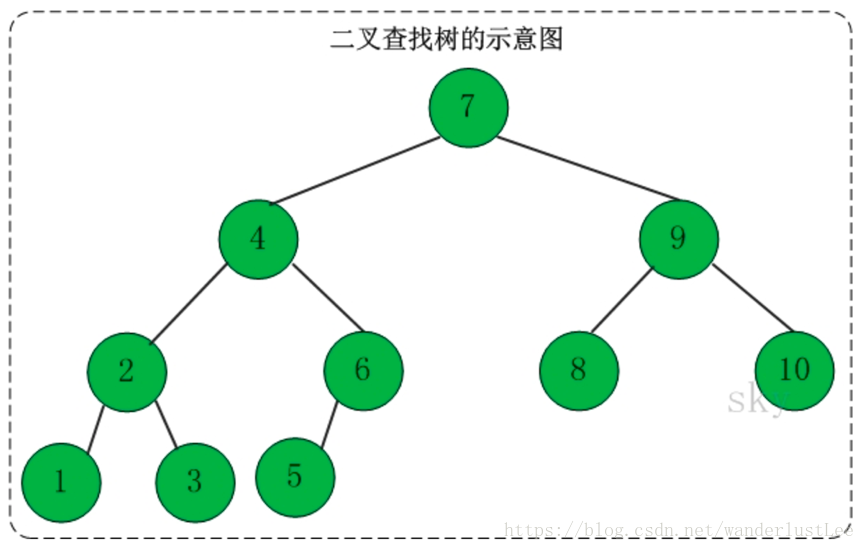
二叉查找树的特点:
1.左子树上所有结点的值均小于它的根结点的值。
2.右子树上所有结点的值均大于它的根结点的值。
3.没有键值相等的结点。








 本文介绍了完全二叉树的定义,强调了叶子节点的分布特点及度为1节点的数量规律。同时,详细阐述了二叉树的前序、中序和后序遍历,分别给出了递归和非递归两种实现方式。二叉查找树也被提及,其特性包括左子树节点值小于根节点,右子树节点值大于根节点,且不存在键值相等的节点。
本文介绍了完全二叉树的定义,强调了叶子节点的分布特点及度为1节点的数量规律。同时,详细阐述了二叉树的前序、中序和后序遍历,分别给出了递归和非递归两种实现方式。二叉查找树也被提及,其特性包括左子树节点值小于根节点,右子树节点值大于根节点,且不存在键值相等的节点。
















 280
280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








