【动态规划】【牛客】[中]BM65. 最长公共子序列(二)

一、题目

 牛客题目链接：BM65 最长公共子序列(二).  要求返回公共子串

LeeCode 题目链接：1143. 最长公共子序列  要求返回公共子串长度

难度等级：中等

题目描述：（牛客）

给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回"-1"。目前给出的数据，仅仅会存在一个最长的公共子序列

数据范围：0≤∣str1∣,∣str2∣≤2000 

要求：空间复杂度 O(n^2) ，时间复杂度 O(n^2) 

示例 1：

 输入： "1A2C3D4B56","B1D23A456A"

 返回值： "123456"

示例 2：

 输入："abc","def"

 返回值："-1"

示例 3：

输入："abc","abc"

返回值："abc"

示例4：

输入： "ab",""

返回值："-1"

二、解题思路&代码实现

题目解读：

• 找到两个字符串的最长公共子序列，子序列不要求位置在原串中连续。
• 仅存在一个最长公共子序列，不需要去重。
• 最长公共子序列为空需要返回"-1"，而不是空序列，最后要变换。
• 注意：子序列不是子串，子串要求所有字符必须连续，子序列不要求连续，只要求相对位置不变。

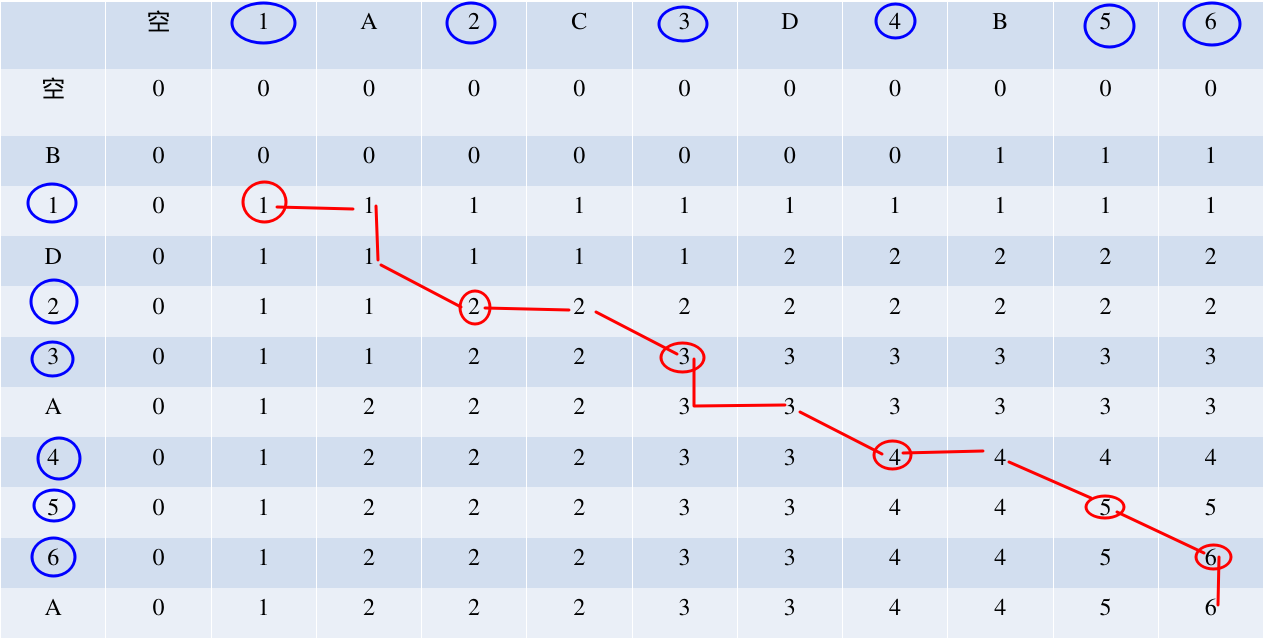
方案一：动态规划+反转字符串（推荐使用，最简单明了）

解题思路：

1. 使用动态规划求解LCS的长度，同时记录路径（用于回溯构造LCS）。
2. 动态规划表dp[i][j]表示str1[0:i]和str2[0:j]的LCS长度。
3. 状态转移方程： 如果str1[i-1] == str2[j-1]，则dp[i][j] = dp[i-1][j-1] + 1 否则，dp[i][j] = max(dp[i-1][j], dp[i][j-1])
4. 构造LCS：从dp表的右下角开始回溯，当str1[i-1]==str2[j-1]时，将该字符加入结果，然后向左上角移动；否则，向LCS长度较大的方向移动（如果dp[i-1][j] >= dp[i][j-1]，则向上移动，否则向左移动）。
5. 注意：如果LCS为空（即长度为0），则返回"-1"。

实现大纲：

1. 边界处理：如果任一输入字符串为空，直接返回"-1"。
2. 动态规划表初始化：
   • 创建 (len1+1) x (len2+1) 的二维数组 dp，其中 dp[i][j] 表示 str1[0:i] 和 str2[0:j] 的最长公共子序列长度。
   • 初始化边界：dp[0][*] = 0 和 dp[*][0] = 0。
3. 填充DP表：
   • 如果当前字符匹配（str1[i-1] == str2[j-1]），则 dp[i][j] = dp[i-1][j-1] + 1。
   • 否则，dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
4. 检查LCS是否为空：如果 dp[len1][len2] == 0，返回"-1"。
5. 回溯构造LCS：
   • 从 dp[len1][len2] 开始，逆序回溯：
     • 如果字符匹配，将字符加入结果，并向左上角移动。
     • 否则，向 dp[i-1][j] 或 dp[i][j-1] 中较大的方向移动（题目保证唯一LCS，因此方向选择不影响结果）。
   • 回溯得到的字符序列是逆序的，需反转后返回。
6. 输出结果：返回构造的LCS字符串。

图示：

复杂度分析：

1. 时间复杂度：O(m × n)

   • 其中 m 和 n 分别是两个字符串的长度。
   • 需要填充一个 m × n 的动态规划表，每个元素的计算时间为 O(1)。
   • 回溯过程的时间复杂度为 O(m + n)，在整体复杂度中可忽略。

2. 空间复杂度：O(m × n)

   • 需要存储一个 m × n 的二维数组 dp。
   • 回溯过程中使用的额外空间为 O(min(m, n))（存储LCS字符），在空间复杂度中可忽略。

代码实现：

golang:

package main

import (
	"fmt"
)

func longestCommonSubsequence(str1, str2 string) string {
	// 如果任一字符串为空，则LCS为空
	if len(str1) == 0 || len(str2) == 0 {
		return "-1"
	}

	len1, len2 := len(str1), len(str2)
	// 创建动态规划表 dp[i][j] 表示 str1[0:i] 和 str2[0:j] 的LCS长度
	dp := make([][]int, len1+1)
	for i := range dp {
		dp[i] = make([]int, len2+1)
	}

	// 填充动态规划表
	for i := 1; i <= len1; i++ {
		for j := 1; j <= len2; j++ {
			if str1[i-1] == str2[j-1] {
				dp[i][j] = dp[i-1][j-1] + 1
			} else {
				// 取上方和左方的最大值
				if dp[i-1][j] > dp[i][j-1] {
					dp[i][j] = dp[i-1][j]
				} else {
					dp[i][j] = dp[i][j-1]
				}
			}
		}
	}

	// 如果LCS长度为0，返回"-1"
	if dp[len1][len2] == 0 {
		return "-1"
	}

	// 回溯构造LCS
	i, j := len1, len2
	var lcs []byte
	for i > 0 && j > 0 {
		if str1[i-1] == str2[j-1] {
			// 字符匹配，加入结果
			lcs = append(lcs, str1[i-1])
			i--
			j--
		} else if dp[i-1][j] >= dp[i][j-1] {
			// 向上移动（选择长度较大的方向）
			i--
		} else {
			// 向左移动
			j--
		}
	}

	// 反转字符序列（因为回溯是逆序的）
	for k := 0; k < len(lcs)/2; k++ {
		lcs[k], lcs[len(lcs)-1-k] = lcs[len(lcs)-1-k], lcs[k]
	}

	return string(lcs)
}

func main() {
	// 测试用例
	fmt.Println(longestCommonSubsequence("abcde", "ace")) // 输出: "ace"
	fmt.Println(longestCommonSubsequence("abc", "def"))   // 输出: "-1"
	fmt.Println(longestCommonSubsequence("", "abc"))      // 输出: "-1"
	fmt.Println(longestCommonSubsequence("abc", ""))      // 输出: "-1"
	fmt.Println(longestCommonSubsequence("abc", "abc"))   // 输出: "abc"
}

java:

public class LongestCommonSubsequence {
    public static String longestCommonSubsequence(String str1, String str2) {
        int m = str1.length();
        int n = str2.length();
        
        // 如果任一字符串为空，返回"-1"
        if (m == 0 || n == 0) {
            return "-1";
        }
        
        // 创建动态规划表 dp[i][j] 表示 str1[0:i] 和 str2[0:j] 的LCS长度
        int[][] dp = new int[m + 1][n + 1];
        
        // 填充动态规划表
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        
        // 检查LCS是否为空
        if (dp[m][n] == 0) {
            return "-1";
        }
        
        // 回溯构造LCS
        StringBuilder lcs = new StringBuilder();
        int i = m, j = n;
        while (i > 0 && j > 0) {
            if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
                lcs.append(str1.charAt(i - 1));
                i--;
                j--;
            } else if (dp[i - 1][j] >= dp[i][j - 1]) {
                i--;
            } else {
                j--;
            }
        }
        
        // 反转字符串
        return lcs.reverse().toString();
    }

    public static void main(String[] args) {
        // 测试用例
        System.out.println(longestCommonSubsequence("abcde", "ace")); // ace
        System.out.println(longestCommonSubsequence("abc", "def"));   // -1
        System.out.println(longestCommonSubsequence("", "abc"));      // -1
        System.out.println(longestCommonSubsequence("abc", ""));      // -1
        System.out.println(longestCommonSubsequence("abc", "abc"));   // abc
    }
}

python:

def longest_common_subsequence(str1: str, str2: str) -> str:
    m, n = len(str1), len(str2)
    
    # 如果任一字符串为空，返回"-1"
    if m == 0 or n == 0:
        return "-1"
    
    # 创建动态规划表
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    
    # 填充动态规划表
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if str1[i - 1] == str2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
    
    # 检查LCS是否为空
    if dp[m][n] == 0:
        return "-1"
    
    # 回溯构造LCS
    i, j = m, n
    lcs = []
    while i > 0 and j > 0:
        if str1[i - 1] == str2[j - 1]:
            lcs.append(str1[i - 1])
            i -= 1
            j -= 1
        elif dp[i - 1][j] >= dp[i][j - 1]:
            i -= 1
        else:
            j -= 1
    
    # 反转字符串
    return ''.join(lcs[::-1])

# 测试用例
print(longest_common_subsequence("abcde", "ace"))  # ace
print(longest_common_subsequence("abc", "def"))    # -1
print(longest_common_subsequence("", "abc"))       # -1
print(longest_common_subsequence("abc", ""))       # -1
print(longest_common_subsequence("abc", "abc"))    # abc

推理解析过程：

1、以 str1 = "abcde", str2 = "ace" 为例的 DP 表

（空间复杂度 O(5×3)=O(15)=O(n²)）

  最终填充结果如下表：

	0	a	c	e
0	0	0	0	0
a	0	1	1	1
b	0	1	1	1
c	0	1	2	2
d	0	1	2	2
e	0	1	2	3

• 空间：5 行 × 4 列 = 20 个整数 → O(5×4)=O(20)=O(n²)（其中 n = max(5,3)=5）
• 时间：5×4=20 次操作 → O(5×4)=O(20)=O(n²)

2、填充过程讲解：

（1）DP 表结构

• 行：str1 的长度 + 1（0 到 5），dp[i][j] 表示 str1[0:i] 和 str2[0:j] 的 LCS 长度
• 列：str2 的长度 + 1（0 到 3），j=0 为虚拟列（空字符串）
• 表格初始状态（第一行/列全为 0）：

  	0	1	2	3
  0	0	0	0	0
  1	0
  2	0
  3	0
  4	0
  5	0

（2）填充过程：

步骤 1：处理 str1[0] = 'a'（行 1）

• j=1：str1[0]=='a' 与 str2[0]=='a' 匹配 → dp[1][1] = dp[0][0] + 1 = 1
• j=2：'a' 与 'c' 不匹配 → max(dp[0][2]=0, dp[1][1]=1) = 1
• j=3：'a' 与 'e' 不匹配 → max(dp[0][3]=0, dp[1][2]=1) = 1

  行 1: [0, 1, 1, 1]

步骤 2：处理 str1[1] = 'b'（行 2）

• j=1：'b' 与 'a' 不匹配 → max(dp[1][1]=1, dp[2][0]=0) = 1
• j=2：'b' 与 'c' 不匹配 → max(dp[1][2]=1, dp[2][1]=1) = 1
• j=3：'b' 与 'e' 不匹配 → max(dp[1][3]=1, dp[2][2]=1) = 1

  行 2: [0, 1, 1, 1]

步骤 3：处理 str1[2] = 'c'（行 3）

• j=1：'c' 与 'a' 不匹配 → max(dp[2][1]=1, dp[3][0]=0) = 1
• j=2：'c' 与 'c' 匹配 → dp[3][2] = dp[2][1] + 1 = 1 + 1 = 2
• j=3：'c' 与 'e' 不匹配 → max(dp[2][3]=1, dp[3][2]=2) = 2

  行 3: [0, 1, 2, 2]

步骤 4：处理 str1[3] = 'd'（行 4）

• j=1：'d' 与 'a' 不匹配 → max(dp[3][1]=1, dp[4][0]=0) = 1
• j=2：'d' 与 'c' 不匹配 → max(dp[3][2]=2, dp[4][1]=1) = 2
• j=3：'d' 与 'e' 不匹配 → max(dp[3][3]=2, dp[4][2]=2) = 2

  行 4: [0, 1, 2, 2]

步骤 5：处理 str1[4] = 'e'（行 5）

• j=1：'e' 与 'a' 不匹配 → max(dp[4][1]=1, dp[5][0]=0) = 1
• j=2：'e' 与 'c' 不匹配 → max(dp[4][2]=2, dp[5][1]=1) = 2
• j=3：'e' 与 'e' 匹配 → dp[5][3] = dp[4][2] + 1 = 2 + 1 = 3

  行 5: [0, 1, 2, 3]

（3）

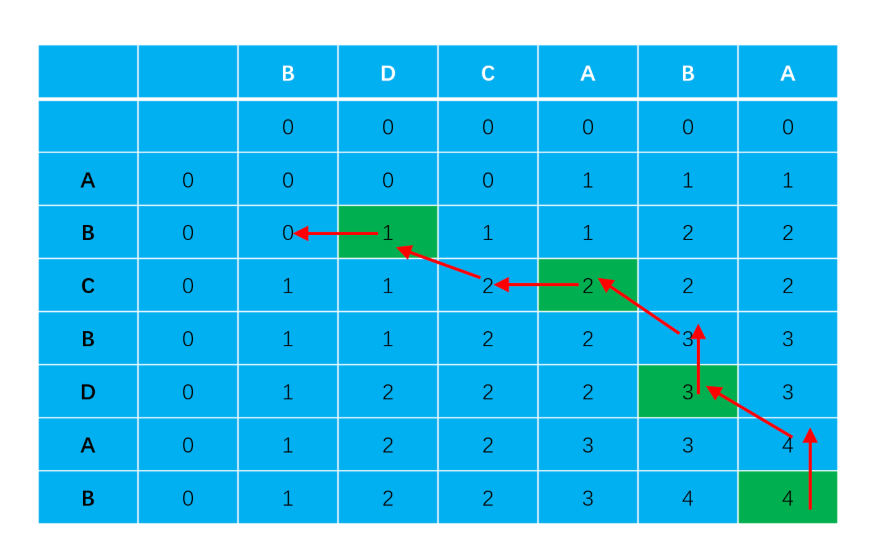
方案二：动态规划+递归获取（推荐使用）

解题思路：

• step 1：优先检查特殊情况。
• step 2：获取最长公共子序列的长度可以使用动态规划，我们以dp[i][j] 表示在s1中以i 结尾，s2中以j 结尾的字符串的最长公共子序列长度。
• step 3：遍历两个字符串的所有位置，开始状态转移：若是i  位与j 位的字符相等，则该问题可以变成1+dp[i−1][j−1] ，即到此处为止最长公共子序列长度由前面的结果加1。
• step 4：若是不相等，说明到此处为止的子串，最后一位不可能同时属于最长公共子序列，毕竟它们都不相同，因此我们考虑换成两个子问题，dp[i][j−1] 或者dp[i−1][j] ，我们取较大的一个就可以了，由此感觉可以用递归解决。
• step 5：但是递归的复杂度过高，重复计算了很多低层次的部分，因此可以用动态规划，从前往后加，由此形成一个表，表从位置1开始往后相加，正好符合动态规划的转移特征。
• step 6：因为最后要返回该序列，而不是长度，所以在构造表的同时要以另一个二维矩阵记录上面状态转移时选择的方向，我们用1表示来自左上方，2表示来自左边，3表示来自上边。
• step 7：获取这个序列的时候，根据从最后一位开始，根据记录的方向，不断递归往前组装字符，只有来自左上的时候才添加本级字符，因为这种情况是动态规划中两个字符相等的情况，字符相等才可用。

图示：

 

复杂度分析：

• 时间复杂度：O(n^2)，构造辅助数组dp与b，两层循环，递归是有方向的递归，因此只是相当于遍历了二维数组
• 空间复杂度：O(n^2) ，辅助二维数组dp与递归栈的空间最大为O(n^2) 

代码实现：

golang:

java:

import java.util.*;
public class Solution {
    private String x = "";
    private String y = "";
    //获取最长公共子序列
    String ans(int i, int j, int[][] b){ 
        String res = "";
        //递归终止条件
        if(i == 0 || j == 0)
            return res;
        //根据方向，往前递归，然后添加本级字符
        if(b[i][j] == 1){
            res += ans(i - 1, j - 1, b);
            res += x.charAt(i - 1);
        }
        else if(b[i][j] == 2)
            res += ans(i - 1, j, b);
        else if(b[i][j] == 3)
            res += ans(i,j - 1, b);
        return res;
    }
    public String LCS (String s1, String s2) {
        //特殊情况
        if(s1.length() == 0 || s2.length() == 0)
            return "-1";
        int len1 = s1.length();
        int len2 = s2.length();
        x = s1;
        y = s2;
        //dp[i][j]表示第一个字符串到第i位，第二个字符串到第j位为止的最长公共子序列长度
        int[][] dp = new int[len1 + 1][len2 + 1];
        //动态规划数组相加的方向
        int[][] b = new int[len1 + 1][len2 + 1];
        //遍历两个字符串每个位置求的最长长度
        for(int i = 1; i <= len1; i++){
            for(int j = 1; j <= len2; j++){
                //遇到两个字符相等
                if(s1.charAt(i - 1) == s2.charAt(j - 1)){
                    //考虑由二者都向前一位
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                    //来自于左上方
                    b[i][j] = 1;
                }
                //遇到的两个字符不同
                else{
                    //左边的选择更大，即第一个字符串后退一位
                    if(dp[i - 1][j] > dp[i][j - 1]){
                        dp[i][j] = dp[i - 1][j];
                        //来自于左方
                        b[i][j] = 2;
                    }
                    //右边的选择更大，即第二个字符串后退一位
                    else{
                        dp[i][j] = dp[i][j - 1];
                        //来自于上方
                        b[i][j] = 3;
                    }
                }
            }
        }
        //获取答案字符串
        String res = ans(len1, len2, b);
        //检查答案是否位空
        if(res.isEmpty()) 
            return "-1";
        else
            return res;
    }
}

python:

import sys
#设置递归深度
sys.setrecursionlimit(100000) 
class Solution:
    def __init__(self):
        self.x = ""
        self.y = ""
    #获取最长公共子序列
    def ans(self, i: int, j: int, b: List[List[int]]): 
        res = ""
        #递归终止条件
        if i == 0 or j == 0: 
            return res
        #根据方向，往前递归，然后添加本级字符
        if b[i][j] == 1:
            res = res + self.ans(i - 1, j - 1, b)
            res = res + self.x[i - 1]
        elif b[i][j] == 2:
            res = res + self.ans(i - 1, j, b)
        elif b[i][j] == 3:
            res = res + self.ans(i, j - 1, b)
        return res
    def LCS(self , s1: str, s2: str) -> str:
        #特殊情况
        if s1 is None or s2 is None: 
            return "-1"
        len1 = len(s1)
        len2 = len(s2)
        self.x = s1
        self.y = s2
        #dp[i][j]表示第一个字符串到第i位，第二个字符串到第j位为止的最长公共子序列长度
        dp = [[0] * (len2 + 1) for i in range(len1 + 1)]
        #动态规划数组相加的方向
        b = [[0] * (len2 + 1) for i in range(len1 + 1)]
        #遍历两个字符串每个位置求的最长长度
        for i in range(1, len1 + 1): 
            for j in range(1, len2 + 1):
                #遇到两个字符相等
                if s1[i - 1] == s2[j - 1]:
                    #考虑由二者都向前一位
                    dp[i][j] = dp[i - 1][j - 1] + 1
                    #来自于左上方
                    b[i][j] = 1 
                #遇到的两个字符不同
                #左边的选择更大，即第一个字符串后退一位
                elif dp[i - 1][j] > dp[i][j - 1]:
                    dp[i][j] = dp[i - 1][j]
                    #来自于左方
                    b[i][j] = 2 
                #右边的选择更大，即第二个字符串后退一位
                else:
                    dp[i][j] = dp[i][j - 1]
                    #来自于上方
                    b[i][j] = 3 
        #获取答案字符串
        res = self.ans(len1, len2, b)
        #检查答案是否位空
        if res is None or res == "":
            return "-1"
        else:
            return res

方案二：动态归划+栈获取（扩展思路）

知识点：

栈是一种仅支持在表尾进行插入和删除操作的线性表，这一端被称为栈顶，另一端被称为栈底。元素入栈指的是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；元素出栈指的是从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

解题思路：

• step 1：优先检查特殊情况。
• step 2：获取最长公共子序列的长度可以使用动态规划，我们以dp[i][j] 表示在s1中以i 结尾，s2中以j 结尾的字符串的最长公共子序列长度。
• step 3：遍历两个字符串的所有位置，开始状态转移：若是ii位与jj位的字符相等，则该问题可以变成1+dp[i−1][j−1] ，即到此处为止最长公共子序列长度由前面的结果加1。
• step 4：若是不相等，说明到此处为止的子串，最后一位不可能同时属于最长公共子序列，毕竟它们都不相同，因此我们考虑换成两个子问题，dp[i][j−1]dp[i][j−1]或者dp[i−1][j]dp[i−1][j]，我们取较大的一个就可以了。
• step 5：得到最长长度后，获取不需要第二个辅助数组b，直接从dp数组最后一位开始，每次比较当前位置与其左、上、左上的关系，然后将符合要求的字符加入栈中，符合要求即来自dp表格左上方的字符。
• step 6：最后将栈中的字符拼接即可得到最长公共子序列，注意检查子序列是否为空。

复杂度分析：

• 时间复杂度：O(n^2) ，最坏复杂度为构造辅助数组dp两层循环.
• 空间复杂度：O(n^2) ，辅助二维数组dp与栈空间最大为O(n^2) .

代码实现：

golang:

package main

import (
	"fmt"
)

// longestCommonSubsequence 返回两个字符串的最长公共子序列
// 如果最长公共子序列为空，则返回"-1"
func longestCommonSubsequence(str1, str2 string) string {
	m, n := len(str1), len(str2)
	
	// 创建 dp 表 (m+1) x (n+1)
	dp := make([][]int, m+1)
	for i := range dp {
		dp[i] = make([]int, n+1)
	}
	
	// 填充 dp 表
	for i := 1; i <= m; i++ {
		for j := 1; j <= n; j++ {
			if str1[i-1] == str2[j-1] {
				dp[i][j] = dp[i-1][j-1] + 1
			} else {
				dp[i][j] = max(dp[i-1][j], dp[i][j-1])
			}
		}
	}
	
	// 检查是否为空
	if dp[m][n] == 0 {
		return "-1"
	}
	
	// 回溯构建最长公共子序列
	var result []byte
	i, j := m, n
	for i > 0 && j > 0 {
		if str1[i-1] == str2[j-1] {
			result = append(result, str1[i-1])
			i--
			j--
		} else if dp[i-1][j] >= dp[i][j-1] {
			i--
		} else {
			j--
		}
	}
	
	// 反转结果（因为回溯是从后往前）
	for k := 0; k < len(result)/2; k++ {
		result[k], result[len(result)-1-k] = result[len(result)-1-k], result[k]
	}
	
	return string(result)
}

// 辅助函数：取最大值
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func main() {
	// 测试用例
	testCases := []struct {
		str1, str2 string
		expected   string
	}{
		{"abcde", "abfce", "ab"},
		{"abc", "ac", "ac"},
		{"abc", "abc", "abc"},
		{"a", "b", "-1"},
		{"abcdef", "zabxyz", "ab"},
		{"aggtab", "gxtxayb", "gtab"},
	}
	
	for _, tc := range testCases {
		result := longestCommonSubsequence(tc.str1, tc.str2)
		fmt.Printf("LCS(%q, %q) = %q (expected: %q)\n", tc.str1, tc.str2, result, tc.expected)
	}
}

java:

import java.util.*;
public class Solution {
    public String LCS (String s1, String s2) {
        //只要有一个空字符串便不会有子序列
        if(s1.length() == 0 || s2.length() == 0) 
            return "-1";
        int len1 = s1.length();
        int len2 = s2.length();
        //dp[i][j]表示第一个字符串到第i位，第二个字符串到第j位为止的最长公共子序列长度
        int[][] dp = new int[len1 + 1][len2 + 1]; 
        //遍历两个字符串每个位置求的最长长度
        for(int i = 1; i <= len1; i++){
            for(int j = 1; j <= len2; j++){
                //遇到两个字符相等
                if(s1.charAt(i - 1) == s2.charAt(j - 1))
                    //来自于左上方
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                //遇到的两个字符不同
                else
                    //来自左边或者上方的最大值
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        //从动态规划数组末尾开始
        int i = len1, j = len2;
        Stack<Character> s = new Stack<Character>();
        while(dp[i][j] != 0){
            //来自于左方向
            if(dp[i][j] == dp[i - 1][j])
                i--;
            //来自于上方向
            else if(dp[i][j] == dp[i][j - 1])
                j--;
            //来自于左上方向
            else if(dp[i][j] > dp[i - 1][j - 1]){
                i--;
                j--;
                //只有左上方向才是字符相等的情况，入栈，逆序使用
                s.push(s1.charAt(i)); 
           }
        }
        String res = "";
        //拼接子序列
        while(!s.isEmpty())
            res += s.pop();
        //如果两个完全不同，返回字符串为空，则要改成-1
        return !res.isEmpty() ? res : "-1";  
    }
}

python:

class Solution:
    def LCS(self , s1: str, s2: str) -> str:
        #特殊情况
        if s1 is None or s2 is None: 
            return "-1"
        len1 = len(s1)
        len2 = len(s2)
        #dp[i][j]表示第一个字符串到第i位，第二个字符串到第j位为止的最长公共子序列长度
        dp = [[0] * (len2 + 1) for i in range(len1 + 1)] 
        #遍历两个字符串每个位置求的最长长度
        for i in range(1, len1 + 1):
            for j in range(1, len2 + 1):
                #遇到两个字符相等
                if s1[i - 1] == s2[j -1]:
                    #来自于左上方
                    dp[i][j] = dp[i - 1][j - 1] + 1
                #遇到的两个字符不同
                else:
                    #来自左边或者上方的最大值
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        #从动态规划数组末尾开始
        i = len1
        j = len2
        s = []
        while dp[i][j] != 0:
            #来自于左方向
            if dp[i][j] == dp[i - 1][j]: 
                i = i - 1
            #来自于上方向
            elif dp[i][j] == dp[i][j - 1]: 
                j = j - 1
            #来自于左上方向
            elif dp[i][j] > dp[i - 1][j - 1]: 
                i = i - 1
                j = j - 1
                #只有左上方向才是字符相等的情况，入栈，逆序使用
                s.append(s1[i]) 
        res = ""
        #拼接子序列
        while len(s) != 0:
            res += s[-1]
            s.pop()
        #如果两个完全不同，返回字符串为空，则要改成-1
        if res is None or res == "": 
            return "-1"
        else:
            return res