[牛客算法]二叉树的后续遍历

一、题目

题目链接：二叉树的后序遍历_牛客题霸_牛客网

题目描述：

给定一个二叉树，返回他的后序遍历的序列。

后序遍历是指按照 左节点->右节点->根节点 的顺序的遍历。

数据范围：二叉树的节点数量满足 1≤n≤100   ，二叉树节点的值满足 1≤val≤100    ，树的各节点的值各不相同。

样例图：

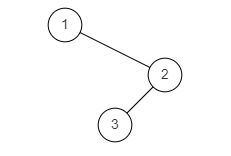
示例1

输入： {1,#,2,3}

返回值：[3,2,1]

示例2

输入：{1}

返回值：[1]

二、思路解析

可以采用二叉树递归遍历方法实现此算法。

首先我们来明确一下二叉树的遍历概念。

二叉树遍历分为：前序遍历、中序遍历、后续遍历。

前序遍历是 根、左节点、右节点 的访问顺序；

中序遍历：是 左节点、根、右节点的访问顺序；

后续遍历： 是左节点、右节点、根的访问顺序；

后续遍历具体实现为：

• step 1：准备数组用来记录遍历到的节点值，Java可以用List，C++可以直接用vector。
• step 2：从根节点开始进入递归，遇到空节点就返回，否则优先进入左子树进行递归访问。
• step 3：左子树访问完毕再进入根节点的右子树递归访问。
• step 4：最后回到根节点，访问该节点。

三、代码实现

java 版本：

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */


public class Solution {
    public int[] postOrderTravel(TreeNode root) {
        List<Integer> list = new ArrayList();
        postOrder(list, root);
        int[] res = new int[list.size()];
        for (int i = 0; i <list.size(); i++) {
            res[i] = list.get(i);
        }
        return res;
    }
    public void postOrder(List<Integer> list, TreeNode root) {
        if (root == null)
            return;
        postOrder(list, root.left);
        postOrder(list, root.right);
        list.add(root.val);
    }
}

Python:

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
#
# @param root TreeNode类
# @return int整型一维数组
#
class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        # write code here
        res = []
        # 递归后续遍历
        self.postOrder(res, root)
        return res

    def postOrder(self, list: List[int], root: TreeNode):
        # 遇到空节点
        if not root:
            return
        ##先左子树
        self.postOrder(list, root.left)
        ##再右子树
        self.postOrder(list, root.right)
        ##最后根节点
        list.append(root.val)

golang:

package main
import . "nc_tools"

/*
 * type TreeNode struct {
 *   Val int
 *   Left *TreeNode
 *   Right *TreeNode
 * }
 */

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 *
 * @param root TreeNode类
 * @return int整型一维数组
 */
func postorderTraversal(root *TreeNode) []int {
	// write code here
	res := make([]int, 0)
	postOrder(&res, root)
	return res
}
func postOrder(res *[]int, root *TreeNode) {
	if root == nil {
		return
	}
	postOrder(res, root.Left)
	postOrder(res, root.Right)
	*res = append(*res, root.Val)
}