二叉树的遍历和算法题_树与二叉树的遍历题目-优快云博客

1.若规定二叉树的根结点的层数为1，那么二叉树的第i层有2^(i-1)棵结点

2.若规定二叉树的根结点的层数为1，那么一颗二叉树最多有2^(h)-1

3.对任意一颗二叉树，如果度为0为n0，度为2为n2，那么n0 = N2+1

4.若规定二叉树的根节点的层数为1，具有n个结点的二叉树，其高度h为log(n+1)

5.对于完全二叉树而已，若将结点从根结点开始，从0开始编号，那么

父节点 = (i-1)/2 (i-1)/2>=0

左孩子结点=(i*2)+1 (i*2)+1<n

右孩子结点=(i*2)+2 (i*2)+2<n

二叉树的结构

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

typedef int BinaryTreeDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BinaryTreeDataType val;
}BTNode;
//二叉树的前序遍历
void PrevOrder(BTNode* bt);
//二叉树的中序遍历
void InOrder(BTNode* bt);
//二叉树的后序遍历
void PostOrder(BTNode* bt);
//二叉树的结点个数
int BTSize(BTNode* bt);
//二叉树的高度
int BTHeight(BTNode* bt);
//二叉树的叶子结点个数
int BTLeafSize(BTNode* bt);
// 二叉树第k层结点个数
int TreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, BinaryTreeDataType x);

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* TreeCreate(BinaryTreeDataType* a, int n, int* pi);
// 二叉树销毁
void TreeDestory(BTNode** root);
// 判断二叉树是否是完全二叉树
bool TreeComplete(BTNode* root);

//二叉树的层序遍历
void LevelOrderTraversal(BTNode* root);

1.二叉树基本功能实现：

二叉树的前中后序遍历：

将空结点表示为N

前序：根 - 左子树 - 右子树

中序：左子树- 根 - 右子树

后序：左子树 - 右子树 - 根

//二叉树的前序遍历
void PrevOrder(BTNode* bt)
{
	if (bt == NULL)
		return;
	printf("%d ", bt->val);
	PrevOrder(bt->left);
	PrevOrder(bt->right);
}
//二叉树的中序遍历
void InOrder(BTNode* bt)
{
	if (bt == NULL)
		return;
	PrevOrder(bt->left);
	printf("%d ", bt->val);
	PrevOrder(bt->right);
}
//二叉树的后序遍历
void PostOrder(BTNode* bt)
{
	if (bt == NULL)
		return;
	PrevOrder(bt->left);
	PrevOrder(bt->right);
	printf("%d ", bt->val);
}

1.1求二叉树的结点个数

当root为空时：返回0

返回当前结点的左子树结点个数和右节点结点个数+1

//二叉树的结点个数
int BTSize(BTNode* bt)
{
	if (bt == NULL)
	{
		return 0;
	}
	return BTSize(bt->left) + BTSize(bt->right) + 1;
}

1.2 求二叉树的高度

为空：返回0

求左子树和右子树中的最大高度，返回最大高度+1

//二叉树的高度
int BTHeight(BTNode* bt)
{
	if (bt == NULL)
		return 0;
	int leftHeight = BTHeight(bt->left);
	int rightHeight = BTHeight(bt->right);
	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

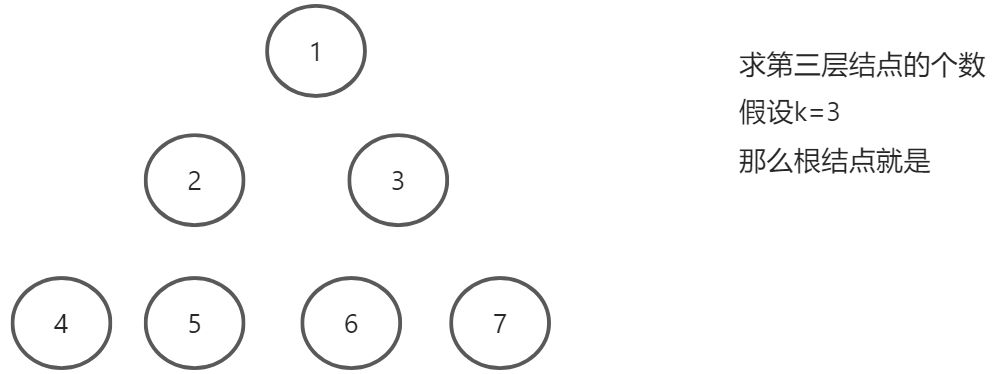
1.3 二叉树第k层结点个数

转化为左右子树的k-1层结点的个数

当k为1时，就是第k层的结点，返回1

当k不等于1或者结点为空时返回0

// 二叉树第k层结点个数
int TreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

1.4 二叉树查找值为x的结点

思路：

1.为空返回NULL

2.当结点的值和x相同时，返回该结点地址

3.用指针接受左右子树的返回值，不为空时返回结点的返回值

注意：需要记录返回值，判断返回值是否为空

// 二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, BinaryTreeDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->val == x)
	{
		return root;
	}
	BTNode* ret1 = TreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}
	BTNode* ret2 = TreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
	return NULL;
}

1.5 二叉树的销毁

思路：

采用后序遍历先把叶子结点free掉，在free掉根结点，因为需要根结点访问左右子树

// 二叉树销毁
void TreeDestory(BTNode** root)
{
	if ((*root) == NULL)
		return;
	TreeDestory(&(*root)->left);
	TreeDestory(&(*root)->right);
	free(*root);
}

1.6 判断二叉树是否是完全二叉树

首先创建一个队列，队列存放二叉树结点的指针，然后将二叉树的根结点push进队列

利用队列先进先出的特性，队头pop的时候将队头的左右子树push进队列，上面带下面

当队列的结点值为NULL时，说明如
// 判断二叉树是否是完全二叉树
bool TreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (QueueFront(&q)!= NULL)
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		if (front != NULL)
		{
			QueueDestory(&q);
			return false;
		}
		QueuePop(&q);
	}
	QueueDestory(&q);
	return true;
}
果是完全二叉树，那么所有结点都进队列了

如果是完全二叉树，那么这时候队列的所有结点都应该是NULL，当有不为NULL的结点就说明树不为完全二叉树

遍历结束说明是完全二叉树

1.7 二叉树的层序遍历

思路：

上一层带下一层

利用队列先入先出的特性，将根结点入队列

循环，队列为空时停止：

保存队头数据

pop队头数据

打印队头数据

出队头数据，判断队头的left和right，若不为空则入队列

//二叉树的层序遍历
void LevelOrderTraversal(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->val);
		if(front->left)
		QueuePush(&q, front->left);
		if(front->right)
		QueuePush(&q, front->right);
	}
	printf("\n");
	QueueDestory(&q);
}

2.二叉树算法题

2.1 二叉树的前序遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）

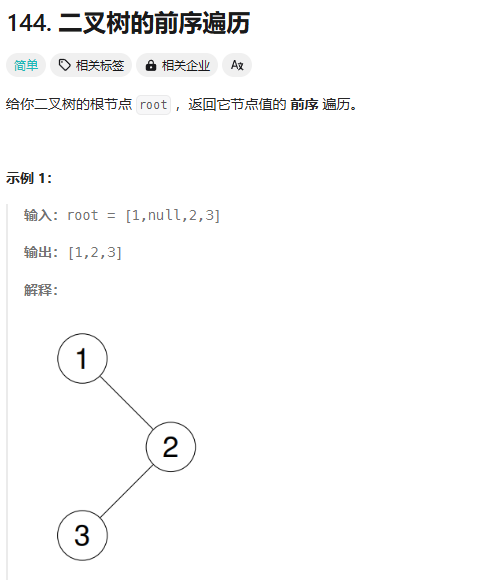
int* preorderTraversal(struct TreeNode* root, int* returnSize)

从root结点遍历二叉树，将前序遍历的结点存放在数组中。

returnSize是输出型参数，存放二叉树的结点个数

思路：

1.求二叉树结点个数

2.开辟结点个数的空间存放结点值

3.遍历二叉树将结点值插入数组

int TreeSize(struct TreeNode* root)
{
    if(root == NULL)
        return 0;
    return TreeSize(root->left) + TreeSize(root->right) + 1;
}
void preOrder(struct TreeNode* root, int* a, int* i)
{
    if(root == NULL)
        return;
    a[(*i)++] = root->val;
    preOrder(root->left,a,i);
    preOrder(root->right,a,i);
    return;
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = TreeSize(root);
    int* ret = (int*)malloc(sizeof(int) * (*returnSize));
    int i = 0;
    preOrder(root, ret, &i);
    return ret;
}

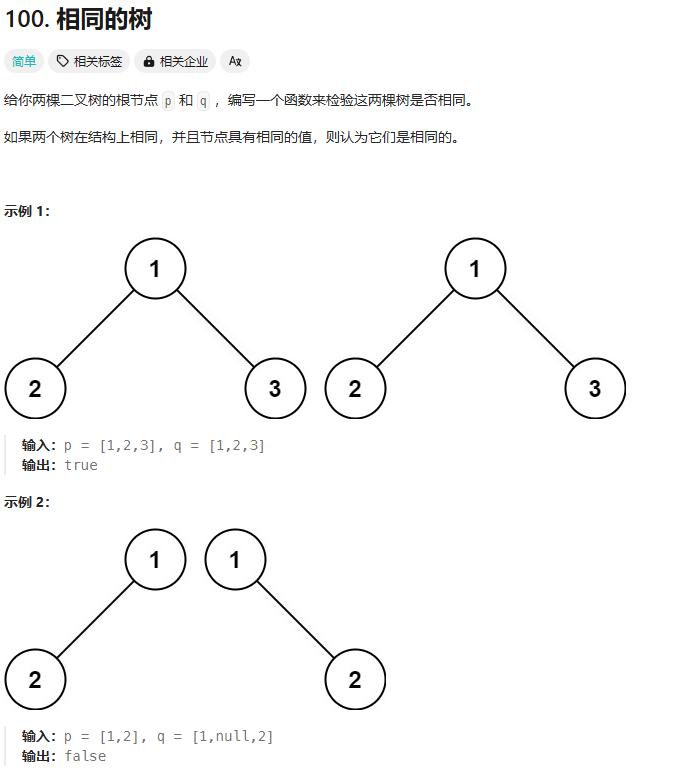
2.2 相同的树

100. 相同的树 - 力扣（LeetCode）

思路：

1.首先对两个根结点判空

2.判断根结点的值是否相同，前序遍历比较

3.当一颗子树为空，另一颗子树不为空时返回false

为空：返回true

不为空：当左子树与右子树的val不同时返回false

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

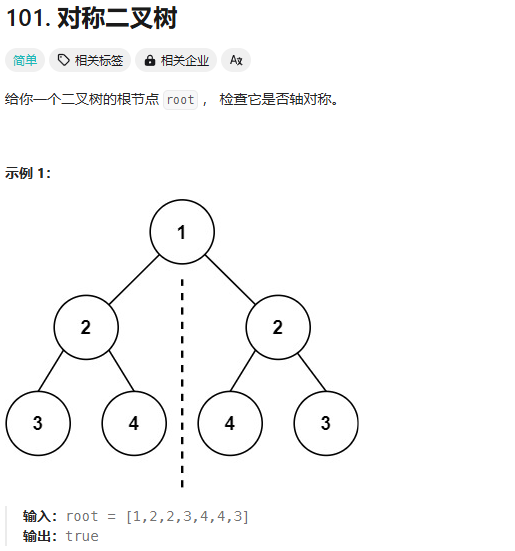
2.3 对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

思路：

1.子函数将左子树和右子树各自当成独立的一棵树，用左子树的left跟右子树的right去进行比较

2.当一颗子树为空，另一颗子树不为空时返回false

bool MyIsSymmetric(struct TreeNode* p,struct TreeNode* q)
{
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
    return MyIsSymmetric(p->left,q->right) && MyIsSymmetric(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root) {
    if(root == NULL)
        return NULL;
    return MyIsSymmetric(root->left, root->right);
}

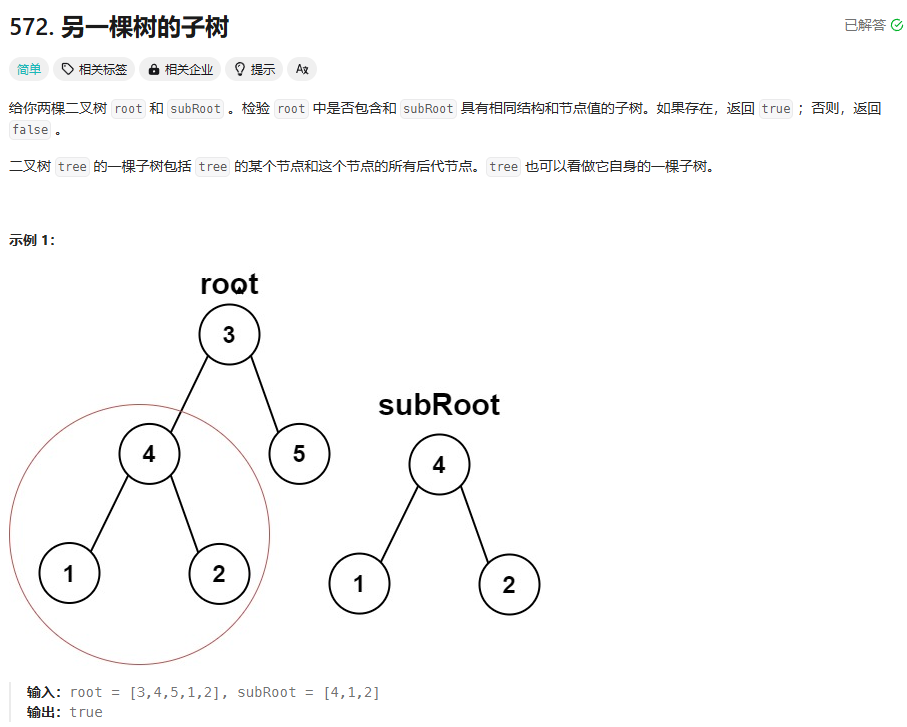
2.4 另一颗树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

思路：

1.判空

2.判断根结点是否与subRoot相同

3.前序遍历，将每一个结点都看作是一颗新的树，与subRoot比较。

4.判断每个结点，当是相同的树时返回true

5.返回值用或者来表示，当两颗树相同时，就不执行另一边。不相同时就继续执行另一边

 bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if(root == NULL)
        return false;
    if(isSameTree(root, subRoot))
    {
        return true;
    }
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

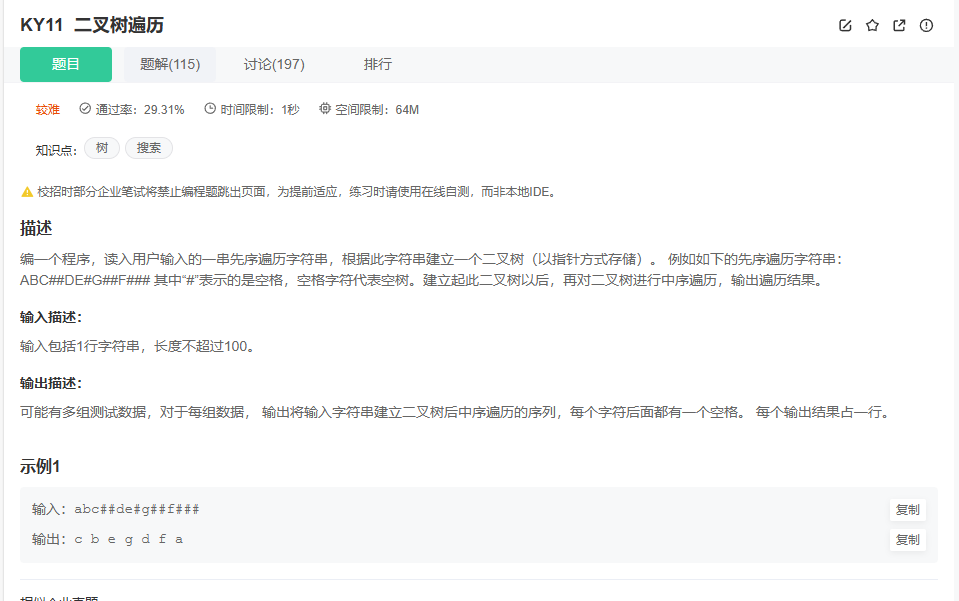
2.5 二叉树遍历

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

思路：

首先需要scanf读入用户输入的数据，用malloc开辟一个100字节的空间

先按照前序遍历把结点的值放入开辟的结点中，再用后序遍历从叶子结点开始链接

i 传指针是因为在递归过程中子树的 i 虽然++了，但是根的 i 还是原来的值，因为i传的是形参

BTNode* CreateNode(char* s, int* i)
{
    if(s[*i] == '#')
    {
        (*i)++;//在里面++,当不为#时下面会++
        return NULL;
    }
    //当在字符串中遍历到一个不为#的字符，就创建结点放入字符
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->val = s[(*i)++];//使用++让下一个函数调用后s的一个字符
    BTNode* left = CreateNode(s,i);//返回左子树的根节点
    BTNode* right = CreateNode(s,i);//返回右子树的根节点

    //后序遍历  走完左子树 右子树 才会到根
    //当走到根时，左子树和右子树已经链接好了
    //最开始从叶子结点开始链接，只不过叶子结点的左右子树都返回NULL
    root->left = left;//让当前结点指向它的左子树
    root->right = right;//让当前结点指向它的左子树
    return root;
}

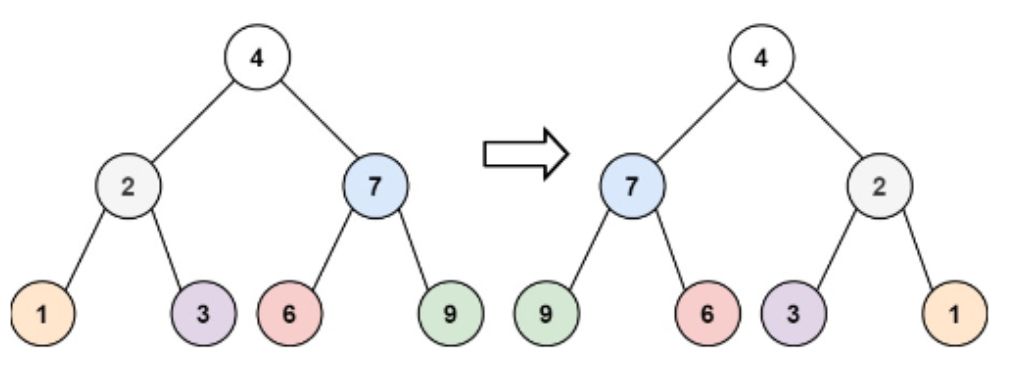
2.6 翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode）

思路：

后序遍历，从叶子结点开始反转

struct TreeNode* invertTree(struct TreeNode* root) {
    if(root == NULL)
        return NULL;
    struct TreeNode* left = invertTree(root->left);
    struct TreeNode* right = invertTree(root->right);
    root->left = right;
    root->right = left;
    return root;
}

2.7 判断一棵树是否是平衡二叉树

110. 平衡二叉树 - 力扣（LeetCode）

首先自底向上递归，判断左右子树是否是平衡二叉树

保存左右子树的返回值，取差值。如果大于1就说明不是平衡二叉树，返回-1

不大于就说明是平衡二叉树，继续向上返回左右子树中大的那一个+1

 int myisBalanced(struct TreeNode* root)
 {
    if(root == NULL)
        return 0;
    int leftHeight = myisBalanced(root->left);
    int rightHeight = myisBalanced(root->right);
    if(leftHeight == -1 ||  rightHeight == -1 || fabs(leftHeight-rightHeight) > 1)
    {
        return -1;
    }
    return fmax(leftHeight,rightHeight) + 1;
 }
bool isBalanced(struct TreeNode* root) {
    if(myisBalanced(root) == -1)
    return false;
    return true;
}