数据结构--并查集

1. 并查集原理

2. 并查集实现

3. 并查集应用

并查集原理

并查集原理

在一些应用问题中，需要 将 n 个不同的元素划分成一些不相交的集合 。 开始时，每个元素自成一个单元素集 合，然后按一定的规律将归于同一组元素的集合合并 。在此过程中 要反复用到查询某一个元素归属于那个集 合的运算 。适合于描述这类问题的抽象数据类型称为 并查集 (union-fifind set) 。

并查集是一个森林--多棵树构成的森林

并查集，多个集合构成，每个集合就可以认为是一棵树

并：合并多个集合

查：两个值是否在一个集合

我们来举一个例子

某公司今年校招全国总共招生 10 人，西安招 4 人，成都招 3 人，武汉招 3 人， 10 个人来自不同的学校，起先互不相识，每个学生都是一个独立的小团体，现给这些学生进行编号：{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体，数组中的数字代表：该小集体中具有成员的个数。( 负号下文解释 )

 此时的-1其实指的是这些数字还没有找到组织，也就是还没有链到树上

毕业后，学生们要去公司上班，每个地方的学生自发组织成小分队一起上路，于是：

西安学生小分队 s1={0,6,7,8} ，成都学生小分队 s2={1,4,9} ，武汉学生小分队 s3={2,3,5} 就相互认识了， 10 个人形成了三个小团体。假设右三个群主0,1,2 担任队长，负责大家的出行。

 一趟火车之旅后，每个小分队成员就互相熟悉，称为了一个朋友圈。

那么我们如何利用并查集去表示这些关系呢？ 

 其实我们只需要改变底下的从属关系，因为6，7，8都是0的队员，也就是子树，所以我们将他们的下标改为其队长的编号，这样就可以找到了，同时我们将队长的下标改为其所在树节点的的数量再取负数即可

那么此时假设我们发生了联谊，使得4要加入0这个团体，此时0与4要合并，并不是这两个值合并，而是他们所在的集合要合并，我们的做法是分别找到这两个值所在集合的根，再去合并

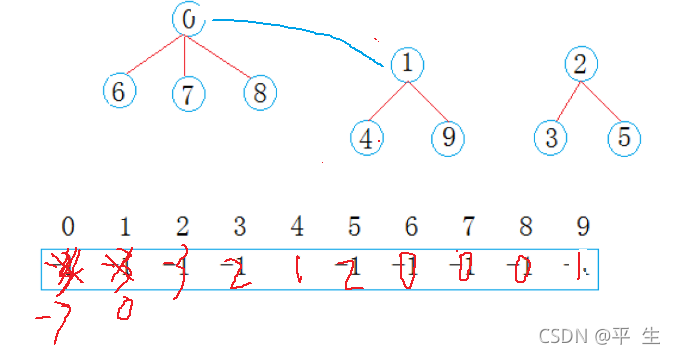
 我们这里的操作就是将1的这棵树链到0上去，将1的下标改为新父亲0，0的下标更新个数为-7，其他不变，便完成了合并

我们有了上面的经验，来看一道题

 我们先来翻译一下他的例子

 

 我们忽略对角线上自己与自己的朋友关系，下标为[0,1]的值为1，代表，0与1是直接朋友，[0,2]为0，代表0与2不是直接朋友，我们将其利用并查集来存储起来，就是我们右边的这个数组，1与0是朋友关系，将0设为根，所以0下标储存的值为-2，也就是团体个数的负值，下标2没有朋友，所以让其数组中存的值为-1，也就是单节点的意思

并查集实现

 我们依据上述想法，对并查集进行代码实现

class UnionFindSet
{
public:
	UnionFindSet(size_t n)
	{
		_ufs.resize(n, -1);
	}
	//x1与x2所在集合合并
	void Union(int x1, int x2)
	{
		assert(x1 < _ufs.size());
		assert(x2 < _ufs.size());

		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		//如果本身就是一个集合，就不合并了
		//如果不在一个集合才需要合并
		if (root1 != root2)
		{
			_ufs[root1] += _ufs[root2];
			_ufs[root2] = root1;
		}
	}
	//查找x所在的集合的根
	int FindRoot(int x)
	{
		assert(x < _ufs.size());
		while (_ufs[x] >= 0)
		{
			x = _ufs[x];
		}
		return x;
	}
private:
	vector<int> _ufs;
};

当我们简单实现了并查集之后，我们再来回过头去看下那道题

class UnionFindSet
{
public:
	UnionFindSet(size_t n)
	{
		_ufs.resize(n, -1);
	}
	//x1与x2所在集合合并
	void Union(int x1, int x2)
	{
		assert(x1 < _ufs.size());
		assert(x2 < _ufs.size());

		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		//如果本身就是一个集合，就不合并了
		//如果不在一个集合才需要合并
		if (root1 != root2)
		{
			_ufs[root1] += _ufs[root2];
			_ufs[root2] = root1;
		}
	}
	//查找x所在的集合的根
	int FindRoot(int x)
	{
		assert(x < _ufs.size());
		while (_ufs[x] >= 0)
		{
			x = _ufs[x];
		}
		return x;
	}
    	size_t SetSize()const
	{
		size_t count = 0;
		for (auto e : _ufs)
		{
			if (e < 0)
				++count;
		}

		return count;
	}
private:
	vector<int> _ufs;
};
class Solution {
public:
	
    int findCircleNum(vector<vector<int>>& isConnected) {
        UnionFindSet ufs(isConnected.size());
        for(size_t i=0;i<isConnected.size();++i)
        {
            for(size_t j=0;j<isConnected.size();++j)
            {
                if(isConnected[i][j]==1)
                {
                    ufs.Union(i,j);
                }
            }
        }
        return ufs.SetSize();
    }
};

并查集应用 

我们再来看一道题

 这道题我们的思路其实也是去利用并查集，因为等式具有传递性，先将所有==的都放进并查集中合并到一个集合，而后再去！=，判断他们不能在一个集合，不过我们这里如果用并查集表示的话，用的都是下标，但是这里给的都是a-z的英文字母，我们采用的方式是直接定址，建立映射，如果再是别的复杂的名字，编号等，我们就需要去建立哈希映射去解决，不过到这里因为数据量较小所以我们还是采用直接定址

我们来对上面的想法进行代码实现

class UnionFindSet
{
public:
	UnionFindSet(size_t n)
	{
		_ufs.resize(n, -1);
	}
	//x1与x2所在集合合并
	void Union(int x1, int x2)
	{
		assert(x1 < _ufs.size());
		assert(x2 < _ufs.size());

		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);

		//如果本身就是一个集合，就不合并了
		//如果不在一个集合才需要合并
		if (root1 != root2)
		{
			_ufs[root1] += _ufs[root2];
			_ufs[root2] = root1;
		}
	}
	//查找x所在的集合的根
	int FindRoot(int x)
	{
		assert(x < _ufs.size());
		while (_ufs[x] >= 0)
		{
			x = _ufs[x];
		}
		return x;
	}
	size_t SetSize()const
	{
		size_t count = 0;
		for (auto e : _ufs)
		{
			if (e < 0)
				++count;
		}

		return count;
	}
private:
	vector<int> _ufs;
};
class Solution {
public:
    bool equationsPossible(vector<string>& equations) {
        UnionFindSet ufs(26);//a-z
        //第一遍，先将相等的值合并到一个集合
        for(const auto& str:equations)
        {
            if(str[1]=='=')
            {
                ufs.Union(str[0]-'a',str[3]-'a');
            }
        }
        //第二遍将不相等的判断在不在一个集合，在就逻辑相悖，不合题意
        for(const auto& str:equations)
        {
            if(str[1]=='!')
            {
                if(ufs.FindRoot(str[0]-'a')==ufs.FindRoot(str[3]-'a'))
                return false;
            }
        }
        return true;
    }
};