零电压开关PWM直流‐直流变换器的设计用于高增益应用
1. 引言
近年来,高电压增益直流‐直流升压变换器已广泛应用于许多工业领域,如不间断电源、分布式光伏发电系统、燃料电池能量转换系统、汽车高强度放电前大灯以及一些医疗设备[1, 2]。
在这些应用中,理论上可以使用传统升压变换器,因为当占空比接近1时,传统升压变换器可实现无穷大的电压增益。然而在实际中,由于主开关和二极管的电流应力、二极管反向恢复问题以及变换器元件相关的寄生元件等因素,升压变换器的实际输出受到限制,无法实现高电压增益。此外,由于占空比微小变化会引起输出电压大幅波动,导致变换器不稳定且瞬态响应缓慢,因此使用高占空比的传统升压变换器并不可行。因此,高占空比的升压变换器会降低整体转换效率,并增加电磁干扰(EMI)。因此,传统升压变换器难以同时实现高升压电压增益和高效率[3, 4]。
过去十年中,许多非隔离拓扑已被研究用于获得高升压电压增益,并避免在极高的占空比下工作[5–20]。这些非隔离转换器包括级联技术[5, 6], 、电压倍压器或倍压器技术[7–9], 、耦合电感技术[9–12], 、开关电感和开关电容技术[13–16], 、电压抬升技术[17, 18],以及电容‐二极管电压倍增器[19, 20],以实现比传统升压变换器在适当占空比下的电压增益更高的增益。
然而,大多数提出的技术都存在较高的开关损耗和导通损耗。这主要是由于高输出电压和高输入电流的基本要求所致。因此,使用高功率额定值的开关器件会导致系统效率降低。耦合电感拓扑似乎是一个很好的候选方案,因为它能够降低开关器件上的电压应力和电流应力。
零电压开关(ZVS)方法适用于大多数载流子半导体器件,例如金属氧化物半导体场效效应晶体管(MOSFETs),因为由输出电容引起的导通损耗较大。近年来,通过在传统脉宽调制(PWM)转换器中增加谐振有源缓冲电路,提出了多种ZVS和零电流开关(ZCS)脉宽调制(PWM)转换器,以结合谐振和常规PWM技术的优点[21–30]。在这些转换器中,导通和/或关断过程仅在极短的时间内实现ZVS和/或ZCS;而在大部分时间内,转换器仍作为常规PWM转换器运行。通过使用ZVS和/或ZCS技术,电磁干扰(EMI)噪声和开关损耗得以降低。然而,这些辅助元件仍然会产生显著的EMI噪声和开关损耗,因为在某些有源缓冲电路中,辅助半导体器件是在硬开关条件下导通和关断的。本文采用了一种ZVS‐PWM开关单元,改善了先前提出的ZVS‐PWM转换器的缺点。辅助开关也在零电流条件(ZCS)下导通,并在零电压条件(ZVS)下关断。通过软开关将开关损耗降至最低,从而提高了升压转换器的效率。提出的转换器具有以下优点:
- 通过使用耦合电感并调节其绕组的匝数比,可有效提高电压增益。
- 通过回收漏感能量,整体效率将得到提升。
- 主功率开关实现零电压开关(ZVS),辅助开关实现零电压开关(ZVS)和零电流开关(ZCS),从而减少开关转换过程中的开关损耗,并提高整体效率。
- 主开关和二极管上的电压应力小于输出电压。
本文的结构如下:第2节介绍了所提出的电路结构。第3节阐述了所提出的变换器的工作原理。第4节详细提取了所提出的变换器的所有稳态特性。第5节描述了实验结果和对比分析。结论在第6节中给出。
2. 电路结构
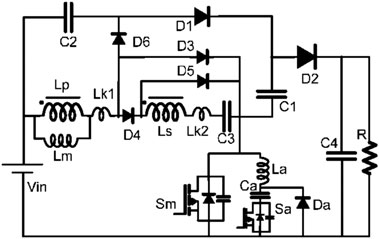
图1给出了所提出的变换器的电路结构。电路元件包括一个直流输入电压 Vin、主开关 Sm、一个耦合电感、辅助开关 Sa,谐振电容Ca、谐振电感La、七个二极管和四个电容器。所提出的变换器结合了两个倍压电路技术和耦合电感,以实现高升压电压增益。通过调节绕组的匝数比,耦合电感可提供高升压电压增益。漏感电感中存储的能量可以被回收,从而提高效率。在信号路径上级联了两个倍压器以增加电压增益。第一个倍压器由Lm、C2, 、D6, 、D1,和C1,组成,第二个倍压器由 Ls、C3,和D5组成。辅助开关的作用是使主开关实现软开关。首先,辅助开关导通并放电主开关的缓冲电容,然后经过短暂的时间延迟,在零电压开关条件下导通主开关。当辅助开关导通时,由谐振电感(La)、谐振电容(Ca)和主开关的缓冲电容构成的谐振回路被接通。借助谐振作用,辅助开关实现零电流开关。当缓冲电容放电完毕后,谐振回路中的电流流过主开关的反并联二极管。此时导通主开关,即可确保实现零电压开关。当谐振电容完全放电后,辅助开关关断。因此,主开关能够
通过零电压开关(ZVS)导通。而辅助开关在零电流条件(ZCS)下导通,在零电压条件(ZVS)下关断。通过软开关技术,开关损耗被最小化,变换器效率得到提高。
3. 工作原理
为简化分析,认为转换器工作在稳态,并做出以下假设:
- 电容器C1和C3足够大,使得电容器电压VC1和VC3在一个开关周期内为恒定值且无纹波。
- 功率MOSFET和二极管被视为简单模型。功率开关被看作是一个具有较小导通电阻、寄生电容和固有体二极管的理想开关。二极管也被视为具有正向电压的理想开关。
- 耦合电感的等效模型包括励磁电感Lm、漏感Lk1和Lk2,以及一个理想变压器(Lp和Ls)。大部分能量存储在励磁电感Lm中,其值大于漏感Lk1和Lk2。耦合电感的匝数比n=为N2/N1。
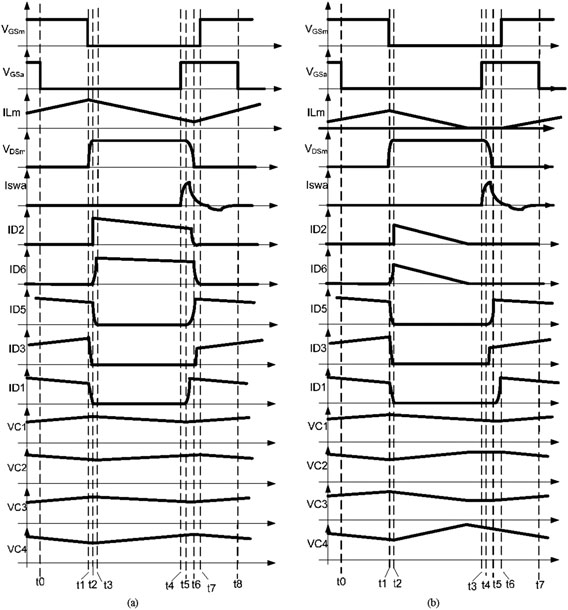
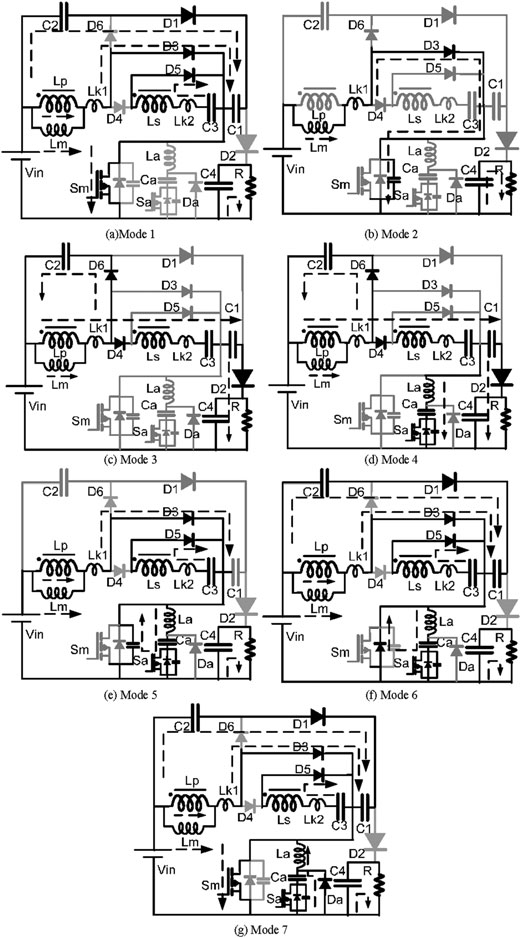
所提出的变换器在连续导通模式(CCM)和断续导通模式(DCM)下的工作原理和稳态分析如下所述。关键波形如图2所示,工作模式如图3所示。
模式 1[t0–t1]
在此模式下,Sm仍处于导通状态。电流通路如图3(a)所示。直流电源能量继续传递给Lm和Lk1,因此iLm和iLk1仍在增加。在该模式结束时,励磁电流iLm达到其最大值。存储在C4中的能量继续向负载放电。二极管D5和D1导通,电容器C3和C1被充电。当Sm关断时,此模式结束。根据图3(a)可写出以下方程:
$$
Vin = VLm + VLk1 + VD3 + RswIL \tag{1}
$$
其中,Rsw 为主开关的导通电阻,VD3 为二极管导通时二极管 D3 的正向电压,IL 为电源电压 Vin 的平均电流。耦合电感 Lm 的励磁电感两端电压、初级漏感电感 LK1 及其关系推导如下:
$$
VLm = Lm \frac{diL}{dt} \tag{2}
$$
$$
VLk1 = Lk1 \frac{diLk1}{dt} = Lk1 \frac{diL}{dt} = Lk1 \frac{VLm}{Lm} \tag{3}
$$
Lm两端的电压由公式(1–3)推导如下:
$$
VLm = k (Vin - VD3 - RswIL) \tag{4}
$$
其中,耦合电感的耦合系数k等于Lm/(Lm+ Lk1)。
模式 2[t1–t2]
在此时间间隔内,Sm和 Sa仍处于关断状态。因此,输入电流流经输出二极管 D3。电流通路如图3(b)所示。主开关 Sm的寄生电容开始充电,iLm和 iLk1开始减小,同时电容 C4中存储的能量继续向负载放电。该模式在二极管 D2开始导通时结束,此模式的持续时间非常短。
模式 3[t2–t3]
在此期间,Sm和Sa仍处于关断状态。电流通路如图3(c)所示。直流电源、Lm、L k1 、Ls、C3 , C1 ,和D2串联连接,将其能量传递给C4和负载。电容C2上的电压也被充电至 $V Lm + VLk1 - V D6$ 或 $\frac{1+nk}{(1 + n)k} VLm - VD6$。根据基尔霍夫电压定律,可推导出以下方程:
$$
Vin = VLm + VLk1 + VD4 + VLs + VLk2 - VC3 - VC1 + VD2 + VO \tag{5}
$$
通过应用基尔霍夫电流定律以及耦合电感中电压、电流与匝数比之间的关系,推导出以下方程:
$$
iLm = iLp + iLk1 \tag{6}
$$
$$
iLk1 = iD6 + iLs = 2iLs = 2iLk2 \tag{7}
$$
$$
iLp = niLs \tag{8}
$$
$$
Lk2 = n^2Lk1 \tag{9}
$$
二次侧漏感电压VLk2如下所示:
$$
VLk2 = Lk2 \frac{diLk2}{dt} = Lk2 \frac{diLk1}{2dt} = n^2Lk1 \frac{diLk1}{2dt} = \frac{n^2}{2} VLk1 \tag{10}
$$
将(6–10)代入(5)得到以下方程:
$$
Vin = VLm \left(\frac{2 + 3nk + n^2}{(2 + n)k}\right) + VD4 - VC3 - VC1 + VD2 + VO \tag{11}
$$
根据上述方程,Lm两端的电压推导如下:
$$
VLm = k \left(\frac{2 + n}{2 + 3nk + n^2}\right)(Vin - VD4 + VC3 + VC1 - VD2 - VO) \tag{12}
$$
该模式以辅助开关Sa的导通结束。
模式 4[t3–t4]
主开关 Sm 关断,由于 La 的存在,辅助开关 Sa 实现零电流开关(ZCS)导通,La 有助于限制辅助电路中电流的上升速率。电流通路如图3(d)所示。该模式下的一阶微分方程由以下方程给出
$$
La \frac{diLa}{dt} + VCa = VO - VC1 \tag{13}
$$
假设在 t4, iLa 时刻谐振电容电压和谐振电感电流为零,且 Vca 由以下给出
$$
VCa(t) = (VO - VC1)[1 - \cos\omega_a(t - t_4)] \tag{14}
$$
$$
iLa(t) = \frac{(VO - VC1)}{Z} \sin\omega_a(t - t_4) \tag{15}
$$
其中 $\omega_a = \frac{1}{\sqrt{L_a C_a}}$ 和 $Z = \sqrt{\frac{L_a}{C_a}}$。
主开关的零电压开关 ,应满足以下条件: $(VO - VC1)/Z > IO$
当谐振电感La与谐振电容Ca发生谐振时,形成由Lm–Ls–La–Ca–Sa–Vin构成的谐振回路。谐振电容被充电至Vo。该模式持续时间很短,当La的电流等于Ls的电流时,该模式结束。
模式 5[t4–t5]
由于 La与 Ca之间的谐振,通过 La的电流继续增加。电流通路如图3(e)所示。存储在 C4 中的能量向负载放电。二极管 D5 导通,电容 C3 被充电。寄生电容中的主开关 Sm的电荷被释放到辅助电路中,当寄生电容 Cs两端的电压为零时,该模式结束,且主开关 Sm的固有体二极管导通。在此模式下,辅助电路电流 iLa继续上升,其值为主输入电流与通过 Cs的电流之和。为简化分析,该模式的时间间隔非常短,且主电感 Lm足够大,可视为恒流源 IO。此模式下的方程如下:
$$
iLm = Cs \frac{dvs}{dt} + iLa \tag{16}
$$
$$
vs = La \frac{diLa}{dt} + vca \tag{17}
$$
其中vs是寄生电容Cs两端的电压。利用初始条件vs(t4)=Vo−Vc1,VLa(t4) = LadiLadt|t=t4代入方程(14),可求解前述方程得到
$$
iLa(t) = \frac{IoCa}{Ca + Cs}[1 - \cos\omega_0(t - t_4)] + Io\cos\omega_0(t - t_4) + \frac{VLa}{Z_0}\sin\omega_0(t - t_4) \tag{18}
$$
$$
vs(t) = (VO - VC1) - \frac{VLaCa}{Ca + Cs}[1 - \cos\omega_0(t - t_4)] + \frac{IO(Ca + Cs)}{t} - \frac{1}{\omega_0}\sin\omega_0(t - t_4) \tag{19}
$$
其中 $\omega_0 = \sqrt{\frac{Cs + Ca}{L_a CsCa}}$ 和 $Z_0 = \sqrt{\frac{L_a}{(Cs + Ca)C_a}}$.
二极管D1导通,为电容C1充电;当寄生电容两端的电压Vs降为零时,该模式结束。
模式 6[t5–t6]
主开关 Sm 实现零电压开关导通。电流通路如图3(f)所示。电容器 C1 和 C3 被充电,存储在 C4 中的能量向负载放电。电容器 C1 两端的电压为
$$
VC1 = Vin + VC2 - VD1 - RswIL \tag{20}
$$
且电容C3两端的电压被充电,其值为
$$
VC3 = kn(Vin - VD3 - RswIL) - VD5 \tag{21}
$$
假设电容器C1和C3足够大,稳态下电容器C1和C3两端电压相对于其平均值VC1和VC3的电压变化可以忽略不计。
模式 7[t6–t7]
在此模式下,电流流过开关Sa的固有体二极管。电流通路如图3(g)所示。如果辅助开关Sa在此区间内关断,则实现零电压开关。当谐振电容Ca完全放电时,该模式结束。
4. 稳态特性
4.1. 连续导通模式运行下的电压增益
在所提出的变换器的稳态运行中,模式2、4、5、6和7的时间间隔与一个开关周期相比非常短,因此在直流电压增益分析中不予考虑。根据电感Lm上的伏秒平衡原理,并结合公式 (5) 和 (14),可推导出以下方程:
$$
(D + \delta)k(Vin - VD3 - RswIL) + (1 - D - \delta)k\left(\frac{2 + n}{2 + 3nk + n^2}\right)(Vin - VD4 + VC3 + VC1 - VD2 - VO) = 0 \tag{22}
$$
其中 δ是从辅助开关闭合到主开关闭合之间的时间。假设辅助电路的谐振频率高于主电路的开关频率。对于无损变换器,k =1,R sw =0 和 V Di =0 i=2,3,4。
无损所提出的变换器的直流电压传输函数(或电压转换比)由下式给出
$$
M_{VDC} = \frac{Vo}{Vin} = \frac{2 + n}{1 - D - \delta} \tag{23}
$$
4.2. 边界工作条件
当磁化电感电流 iLm在开关关断期间减小到零时,该转换器工作在DCM模式。作为一种特殊情况,当电流 iLm在 t=Ts 时刻减小到零时,电路工作在CCM和DCM的边界。当电路工作在边界状态时,电流 iLm的变化由公式(5)推导得出。电感 iLm两端的电压为
$$
Lm \frac{diL}{dt} = VLm = k(Vin - VD3 - RswiL) \tag{24}
$$
因此,通过电感Lm的电流为
$$
iLm(t) = \frac{Vin - VD3}{Rsw}(1 - e^{-t/\tau}) + iLm(0) \tag{25}
$$
其中 $\tau = \frac{Lmk}{Rsw}$,且 iLm(0) 为电感 Lm 在时刻 t = 0 的初始电流,在边界状态下为零。假设 $\tau \gg Ts$ 且 $e^{-t/\tau} \approx 1 - t/\tau$,则电感 Lm 的峰峰值纹波电流为
$$
iLm(DTs) = \frac{k(Vin - VD3)}{Lm}(D + \delta)Ts \tag{26}
$$
iLm、iLs 和 Io 之间的电流关系由以下给出
$$
iLm = (2 + n)iLs \tag{27}
$$
$$
Io = \frac{Vo}{R} = iLs(1 - D - \delta) \tag{28}
$$
因此,在边界条件下,励磁电感Lm与负载电流Io之间的关系为
$$
Io = \frac{Vo}{R} = \frac{k(Vin - VD3)}{Lm(2 + n)}(D + \delta)(1 - D - \delta)Ts \tag{29}
$$
与[3]中讨论的方法类似,通过一些简化假设,可得到确保在任意占空比D下均实现CCM工作的电感L的最小值
$$
L_{min} = \frac{2}{27} \frac{Vo}{(2 + n)^2IoB_{max}}Ts = \frac{2}{27} \frac{RL_{max}}{(2 + n)^2}Ts \tag{30}
$$
确保在任意D值下实现DCM工作的电感L的最大值可表示为
$$
L_{max} = \frac{RL_{min}}{2(2 + n)^2}Ts \min\left{DB_{min}(1 - DB_{min})^2, DB_{max}(1 - DB_{max})^2\right} \tag{31}
$$
零电压开关PWM直流‐直流变换器的设计用于高增益应用
4. 稳态特性(续)
4.3. 功率器件上的电压和电流应力
开关和二极管在连续导通模式下稳态运行时的最大电压和电流应力
$$
V_{sm} = V_{D2} = V_{D1} = \frac{n+1}{n+2}Vo \tag{32}
$$
$$
V_{D6} = V_{C1} = \frac{Vo}{n+2} \tag{33}
$$
$$
V_{D3} = V_{D5} = nVin - \frac{n}{n+2}Vo \tag{34}
$$
$$
I_{D2} = I_o \tag{35}
$$
在连续/断续导通模式边界处的电感电流峰峰值
$$
\Delta i_L = \frac{k(Vin - V_{D3})}{L_m}(D + \delta)Ts \tag{36}
$$
$$
I_{D3} = I_{D4} = I_{sm} = \frac{(2 + n)I_o}{1 - D - \delta} + \frac{\Delta i_L}{2} \tag{37}
$$
其中$I_{sm}$是主开关的峰值电流。
4.4. 断续导通模式运行下的电压增益
为简化断续导通模式(DCM)的分析,忽略耦合电感的所有漏感。耦合电感被建模为一个励磁电感$L_m$和一个理想变压器。所有半导体器件均视为理想器件。如图4所示,DCM工作模式在一个开关周期内可分为三种工作模式。参考图4并利用伏秒平衡,
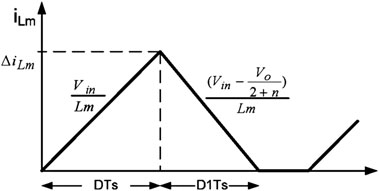
$$
VinDT_s + \left(Vin - \frac{Vo}{2 + n}\right)D_1T_s = 0 \tag{38}
$$
导致$M_{VDC} = \frac{Vo}{Vin} = \frac{I_{in}}{I_o} = (2 + n)\left(1 + \frac{D}{D_1}\right)$。峰峰值电流为
$$
\Delta i_{Lm} = i_{Lm}(DT_s) = \frac{VinDT_s}{L_m} = \frac{VoDT_s}{L_mM_{VDC}} \tag{39}
$$
直流输入电流是通过电感电流的平均值得到的
$$
I_{in} = \frac{1}{T_s} \int_0^{T_s} i_{Lm}dt = \frac{(D + D_1)\Delta i_{Lm}}{2} = \frac{(D + D_1)DVoT_s}{2L_mM_{VDC}} = \frac{D^2VoT_s}{2L_m(M_{VDC} - (2 + n))} \tag{40}
$$
由此
$$
\frac{Vo}{RL} = I_o = \frac{I_{in}}{M_{VDC}} = \frac{D^2VoT_s}{2L_mM_{VDC}} \cdot \frac{1}{M_{VDC} - (2 + n)} \tag{41}
$$
因此,所提出的变换器在断续导通模式下的直流电压传输函数,
$$
M_{VDC} = \frac{Vo}{Vin} = \frac{(2 + n) + \sqrt{(2 + n)^2 + \frac{2RLT_sD^2}{L_m}}}{2} \tag{42}
$$
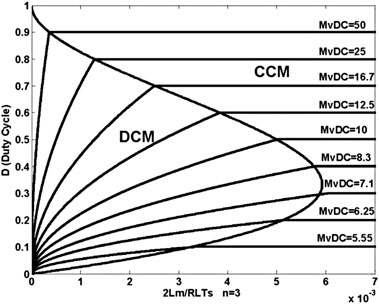
4.5. 所提出的变换器在连续导通模式和断续导通模式下的纹波电压
该提出的转换器可以在连续导通模式或断续导通模式下运行。在本节中,详细介绍了电容电压降对连续导通模式和断续导通模式下输出电压纹波的影响。
4.5.1 连续导通模式运行下的纹波电压
参考图2和3在稳态运行时的情况,开关导通期间,电容器C1和C3两端的电压分别被充电至 $\frac{Vin}{1-D}$和n倍输入电压。在开关关断期间,由于电容电压 $V_{C1}$和$V_{C3}$被电流$i_{Ls}$放电,其电压应下降至 $\Delta V_{c1}$和$\Delta V_{c3}$,其中$i_{Ls}$为流经副边的电流。
$$
V_{C1} = \frac{Vin}{1 - D} - \Delta V_{C1} = \frac{Vin}{1 - D} - \frac{(1 - D)}{C_1}T_si_{Ls} \tag{43}
$$
$$
V_{C3} = nVin - \Delta V_{C3} = nVin - \frac{(1 - D)}{C_3}T_si_{Ls} \tag{44}
$$
在开关关断期间,电感电流 $i_{Ls}$ 为
$$
i_{Ls} = I_o + i_{C2} = I_o + \frac{D}{1 - D}I_o = \frac{I_o}{1 - D} \tag{45}
$$
利用电感$L_m$上的伏秒平衡原理,可得到以下关系:
$$
\frac{DT_s}{L_m}Vin = \frac{(1 - D)T_s}{(1 + n)L_m}(Vo - V_{C1} - V_{C3} - Vin) \tag{46}
$$
将(43–45)代入(46)得到以下方程:
$$
Vo = \frac{(2 + n)}{1 - D}Vin \Bigg/ \left(1 + \frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right)\right) \tag{47}
$$
如果我们假设这个条件,
$$
\frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right) \ll 1 \tag{48}
$$
然后,输出电压可以估计为
$$
Vo = V_{oDC} - \Delta V_o = \frac{(2 + n)}{1 - D}Vin \left(1 - \frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right)\right) \tag{49}
$$
因此,由于C1和C3,输出电压降可以按如下方式估算
$$
\Delta V_o = \frac{(2 + n)}{1 - D}Vin \cdot \frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right) = \frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right)Vo \tag{50}
$$
在开关导通期间,二极管 $D_2$ 截止。因此,输出电流由电容器 $C_4$ 放电提供。电容器 $C_4$ 两端的电压(即输出电压)必须下降。输出电压降的计算公式为
$$
\Delta V_{C4} = \frac{DT_s}{C_4}I_o = \frac{DT_s}{C_4} \cdot \frac{Vo}{R_L} \tag{51}
$$
综合电容器 $C_1$, $C_3$, 和 $C_4$, 引起的影响,可得输出电压的总变化量 $\Delta V_o$ 为
$$
\Delta V_o = \left(\frac{1}{C_1} + \frac{1}{C_3} + \frac{D}{C_4}\right) \cdot \frac{VoT_s}{R_L} \tag{52}
$$
通常,电容器C1和C3大于电容器C4,,且占空比D恒小于1,因此电容器C1和C3的影响大于电容器C4。
4.5.2. 断续导通模式下的纹波电压
对于DCM的纹波电压分析与CCM类似。通过参考图2和图3并应用伏秒平衡原理,采用与CCM类似的方法,可推导出以下方程:
$$
\Delta V_{C1} = \frac{D_1}{C_1}T_si_{Ls} = \frac{T_s}{C_1} \cdot \frac{Vo}{R_L} \tag{53}
$$
$$
\Delta V_{C3} = \frac{D_1}{C_3}T_si_{Ls} = \frac{T_s}{C_3} \cdot \frac{Vo}{R_L} \tag{54}
$$
$$
\Delta V_{C4} = \frac{(D + D_2)}{C_4}T_sI_o = \frac{(1 - D_1)T_s}{C_4} \cdot \frac{Vo}{R_L} \tag{55}
$$
$$
Vo = \frac{(2 + n)(D + D_1)}{D_1}Vin \Bigg/ \left(1 + \frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right)\right) \tag{56}
$$
$$
Vo = M_{VDC}Vin \left(1 - \frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right)\right) \tag{57}
$$
其中$M_{VDC}$是所提出的变换器在DCM下的直流电压传输函数。因此,DCM运行时的输出纹波为
$$
\Delta V_o = M_{VDC} \cdot \frac{T_s}{R_L}\left(\frac{1}{C_1} + \frac{1}{C_3}\right)Vin + \frac{(1 - D_1)T_s}{C_4} \cdot \frac{Vo}{R_L} \tag{58}
$$
4.6. 效率分析
为了简化所提出的变换器的效率分析,假设在计算中未加入包含La、Ca和辅助开关的零电压开关部分。因此,工作原理分为两种模式;图6显示了所提出的变换器包含寄生元件的等效电路,其中$r_{DS}$为MOSFET导通电阻,$R_{Fi}$为第i个二极管正向电阻,$V_{Di}$为第i个二极管阈值电压,$r_{L1}$和$r_{L2}$分别为耦合电感初级和次级绕组的等效串联电阻(ESR)。导通损耗的评估将假设电感电流$i_{Lm}$无纹波,并等于直流输入电流$I_{Lm}$。
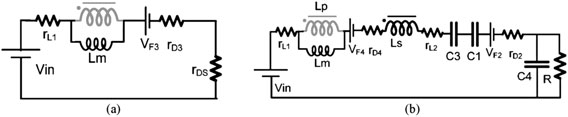
4.6.1 连续导通模式运行下的效率
当主开关导通时,等效电路如图6(a)所示。通过对C4应用安秒平衡原理,并获得$V_{Lm}$的平均值。
$$
V_{Lm} = Vin - V_{D3} - I_1(r_{L1} + r_{D3}) - I_2r_{DS} \tag{59}
$$
其中
$$
I_1 = \left[\frac{(n+2)}{(1 - D)} + \frac{n}{D}\right]I_o \tag{60}
$$
$$
I_2 = \left[\frac{(n+2)}{(1 - D)} + \frac{(n+1)}{D}\right]I_o \tag{61}
$$
当主开关关断时,等效电路如图6(b)所示。$V_{Lm}$的平均值可表示为
$$
(1 + n)V_{Lm} = Vin - V_{D4} - V_{D2} + V_{C3} + V_{C1} - I_3(r_{L2} + r_{D4} + r_{D2}) - I_4r_{L1} - Vo \tag{62}
$$
其中
$$
I_3 = \frac{I_o}{(1 - D)} \tag{63}
$$
$$
I_4 = \frac{2I_o}{(1 - D)} \tag{64}
$$
对$L_m$应用伏秒平衡原理可得
$$
M_{VDC-CCM} = \frac{Vo}{Vin} = \frac{n+2 - B/Vin}{A(1+n)R_L} + (1 - D) \tag{65}
$$
其中
$$
A = \frac{2r_{L1} + r_{L2} + r_{D4} + r_{D2}}{(1 + n)} + D\left \frac{(2 + n)}{(1 - D)} + n\right + r_{DS} \tag{66}
$$
$$
B = D(n+1)V_{D3} + (1 - D)(V_{D4} + V_{D2}) \tag{67}
$$
所提出的变换器的输入功率和输出功率可表示为
$$
P_{in} = DVin I_{in(on)} + (1 - D)Vin I_{in(off)} = (2 + n)Vin \frac{I_o}{(1 - D)} \tag{68}
$$
$$
P_o = V_o I_o = \frac{V_o^2}{R_L} \tag{69}
$$
因此,连续导通模式下的转换器效率为
$$
\eta = \frac{P_o}{P_{in}} = \frac{(1 - D)}{(2 + n)M_{VDC-CCM}} \tag{70}
$$
4.6.2 断续导通模式运行下的效率
DCM的效率分析与CCM类似。通过参考图6并应用伏秒平衡原理,采用与CCM类似的方法,推导出以下方程:
$$
V_{Lm} = Vin - V_{D3} - I_1(r_{L1} + r_{D3}) - I_2r_{DS} \tag{71}
$$
$$
(1 + n)V_{Lm} = Vin - V_{D4} - V_{D2} + V_{C3} + V_{C1} - I_3(r_{L2} + r_{D4} + r_{D2}) - I_4r_{L1} - Vo \tag{72}
$$
其中
$$
I_1 = \left[\frac{(n+2)}{D_1} + \frac{n}{D}\right]I_o \tag{73}
$$
$$
I_2 = \left[\frac{(n+2)}{D_1} + \frac{(n+1)}{D}\right]I_o \tag{74}
$$
$$
I_4 = 2I_3 = \frac{2I_o}{D_1} \tag{75}
$$
利用伏秒平衡原理对$L_m$进行分析可得
$$
M_{VDC-CCM} = \frac{Vo}{Vin} = \frac{(n+1)(D + D_1) + 1 - B/Vin}{A(1+n)R_L} + D_1 \tag{76}
$$
其中
$$
A = \frac{2r_{L1} + r_{L2} + r_{D4} + r_{D2}}{(1 + n)} + D\left \frac{(2 + n)}{D_1} + n\right + r_{DS} \tag{77}
$$
$$
B = D(n+1)V_{D3} + D_1(V_{D4} + V_{D2}) \tag{78}
$$
断续导通模式下的变换器效率为
$$
\eta = \frac{P_o}{P_{in}} = \frac{D_1(n+2)}{(D + D_1)M_{VDC-DCM}} \tag{79}
$$
5. 实验结果
实验样机电路已实现,以验证所提出的变换器的性能。该转换器的构建规格如下:Vin = 12,主开关的占空比为= 50%,辅助开关的占空比为= 20%,主开关与辅助开关之间的延迟时间为 = 0.05Tsw,开关频率f sw = 100 kHz。延迟时间根据谐振电感La和谐振电容Ca的值选择,以确保辅助开关实现零电压开关。
从东京电气化学工业株式会社(TDK)的数据手册中,我们选择适当尺寸的ETD‐19磁芯(Ae= 0.413 cm²,Wa= 70.5 mm²,Ve= 22.53 cm³,和AL= 1720nH/N²)以最小化铁芯损耗。表I中列出的元件被用于制作样机。
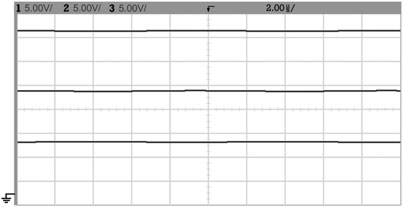
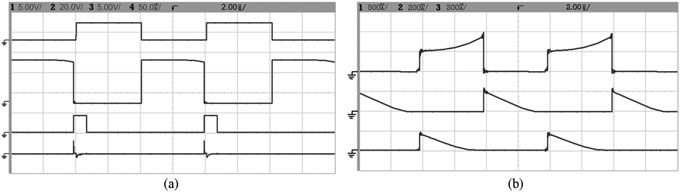
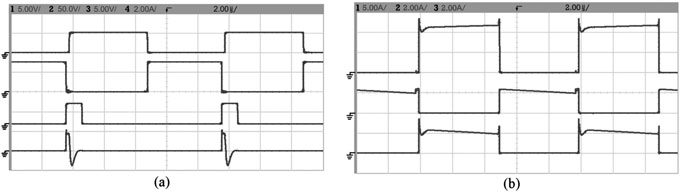 主开关栅极电压波形、主开关漏极电压波形Vds、辅助开关栅极电压波形以及谐振电感电流波形。(b) 二极管D3、D4和D5的电流波形。)
主开关栅极电压波形、主开关漏极电压波形Vds、辅助开关栅极电压波形以及谐振电感电流波形。(b) 二极管D3、D4和D5的电流波形。)
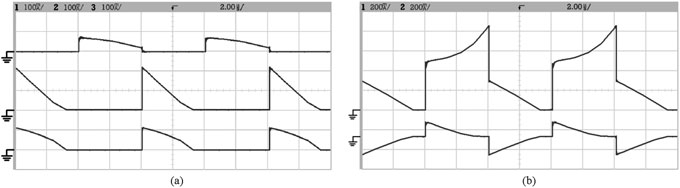
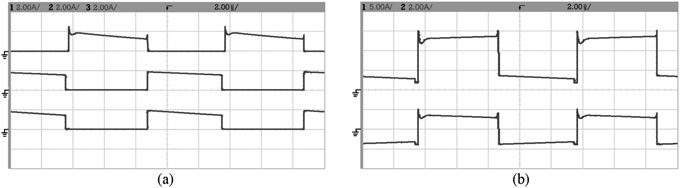 二极管D1、D2和D6的电流波形。(b) 耦合电感初级侧和次级侧的电流波形。)
二极管D1、D2和D6的电流波形。(b) 耦合电感初级侧和次级侧的电流波形。)
 主开关栅极电压波形、主开关漏极电压波形Vds、辅助开关栅极电压波形以及谐振电感电流波形。(b) 二极管D3、D4和D5的电流波形。)
主开关栅极电压波形、主开关漏极电压波形Vds、辅助开关栅极电压波形以及谐振电感电流波形。(b) 二极管D3、D4和D5的电流波形。)
 二极管D1、D2和D6的电流波形。(b) 耦合电感初级侧和次级侧的电流波形。)
二极管D1、D2和D6的电流波形。(b) 耦合电感初级侧和次级侧的电流波形。)
与提出的
| 表I. 样机电路的参数和组件。 |
|---|
| 输入电压 |
| 输出电压 |
| 输出功率 |
| 开关频率 |
| 耦合电感 |
| 电感 |
| 电容器 |
| 开关 |
| 二极管 |
| 表II. 占空比= 0.5和输出功率= 120W下的部分实验结果。 |
|---|
| Vin |
| $V_{c1}$ |
| $V_{c2}$ |
| $V_{c3}$ |
| $V_{out}$ |
| 表III. 所提出的变换器与其他变换器的比较。 |
|—|—|—|—|—|—|—|—|—|—|—|
| | [2] | [9] | [18] | [31] | [32] | [33] | [34] | [35] | [36] | 提出的 |
| 耦合电感/变压器 | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | No | Yes |
| 电容器数量 | 4 | 2 | 4 | 2 | 4 | 4 | 3 | 5 | 3 | 5 |
| $M_{VDC} = \frac{V_o}{V_{in}}$ | $\frac{2+n}{(1-D)^2}$ | $\frac{2(1+nD)}{1-D}$ | 匝数比 $\frac{2}{(1-D)}$ | $\frac{1+nD}{1-D}$ | $\frac{1+n}{1-D}$ | $\frac{1+n}{1-D}$ | $\frac{1+n}{1-D}$ | $\frac{2+nD}{1-D}$ | $\frac{3-D}{1-D}$ | $\frac{2+n}{1-D}$ |
| 二极管的应力 | $(1+n)V_o$ | $\frac{2+n}{2}V_o$ | $nVin$ | $Vo - nVin$ | $Vo - V_{in}$ | $\frac{1-D}{nV_o}$ | $\frac{1+n}{nV_{in}}$ | $\frac{1-D}{Vo - nDV_{in}}$ | $\frac{1-D}{Vo - V_{in}}$ | $\frac{nV_o}{2+n}$ |
| 开关的应力 | $V_o$ | $\frac{2+n}{2}V_o$ | 在 $V_{in}$ 上 | $2V_o$ | $\frac{1-D}{V_{in}}$ | $\frac{1-D}{V_o}$ | $\frac{1+n}{V_{in}}$ | $\frac{1-D}{Vo - 2nDV_{in}}$ | $\frac{2(1-D)}{V_o - V_{in}}$ | $\frac{(1+n)匝数比 V_o}{2+n}$ |
| ZVS | No | No | No | Yes | Yes | Yes | No | No | No | Yes |
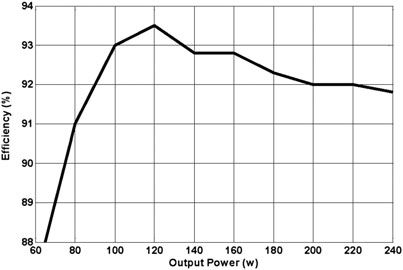
| 效率 (120 W) | 92.5 | 92.5 | 94 | 90 | 95.5 | 94.2 | – | 92.3 | – | 93.5 |
与传统转换器相比,可以看出效率有所提高。然而,由于所提出的变换器使用了更多的电路元件,导致成本较高。所提出的变换器的性能和能力也通过与其他高升压转换器的分析比较得到了验证。为了简化讨论,假设所有转换器均工作在连续导通模式。表III总结了所提出的变换器及其他转换器的规格。
6. 结论
本文提出了一种高升压直流‐直流变换器。所提出的变换器通过集成耦合电感和倍压电路,通过调节绕组的匝数比来实现高升压电压增益,并避免占空比D取值过高。由于回收了耦合电感漏感电感中存储的能量,并且主开关在零电压开通下工作,辅助开关在零电流开通和零电压关断下工作,从而降低了开关损耗,因此所提出的变换器具有高效率。文中详细讨论了所提出的变换器在连续导通模式和断续导通模式下的特性,以及电压增益、边界工作条件、输出电压纹波和效率分析的稳态分析。最后,通过仿真和实验结果,在实验室构建了所提出的变换器的样机电路,以验证其功能并确认所提出的理论分析。




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








