流注放电，COMSOL放电仿真，等离子体仿真，棒板电极，空气流注，流注放电，需要拿去参考。

标题：流注放电与COMSOL放电仿真：揭示等离子体仿真之谜

引言

在电力、电气和电子领域，流注放电现象及其背后的等离子体行为一直是一个热门的研究话题。这种独特的放电模式涉及到电子的移动、离子生成和场强的复杂相互作用，对我们的工业生产和生活环境产生深远影响。本文将探讨流注放电的原理，以及如何使用COMSOL等仿真工具来模拟和分析这一过程。

一、流注放电的基本原理

流注放电是一种常见的气体放电现象，其基本原理是空气或其他气体在强电场作用下发生电离，形成电子和正负离子的混合物，即等离子体。这种等离子体在电场的作用下形成流注，进而引发放电。流注放电在雷电、电器开关操作、静电放电等自然和工业过程中都可能出现。

二、COMSOL放电仿真

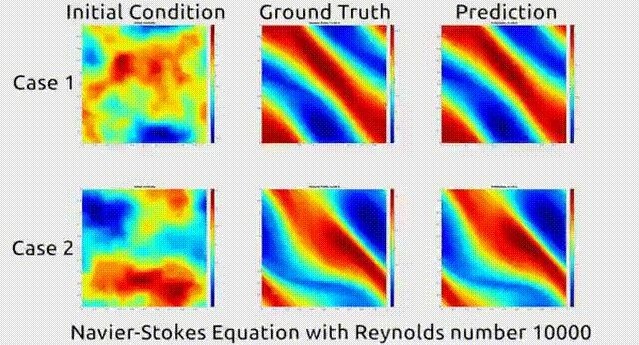
为了更好地理解和分析流注放电过程，我们引入了COMSOL这一强大的仿真工具。COMSOL是一款广泛应用于物理、工程和生物医学等领域的仿真，尤其擅长解决多物理场问题。在放电仿真中，COMSOL可以通过数学模型和算法来模拟电场、磁场、电流和电荷的分布，从而预测和分析流注放电的过程和结果。

三、棒板电极与空气流注

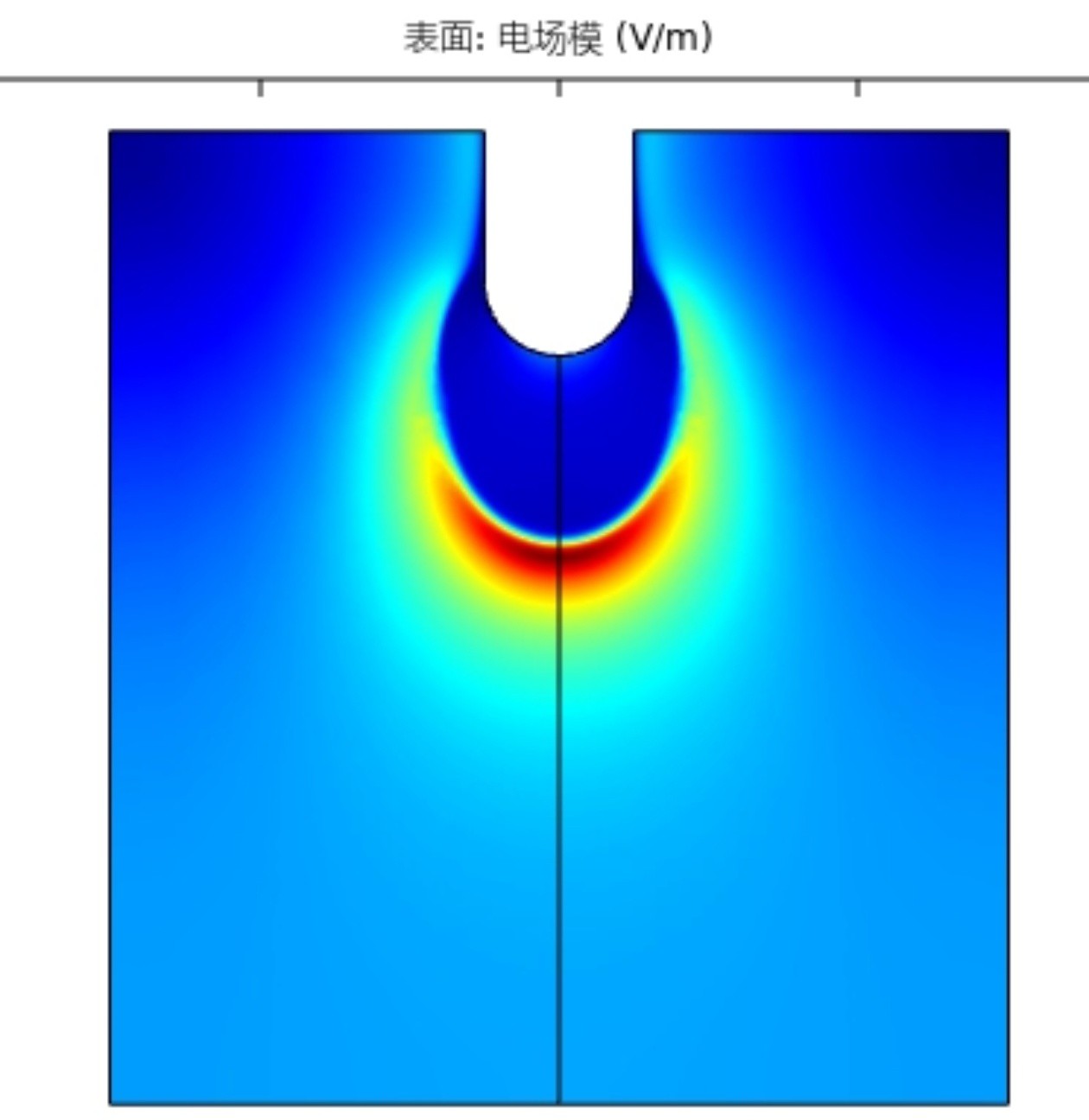
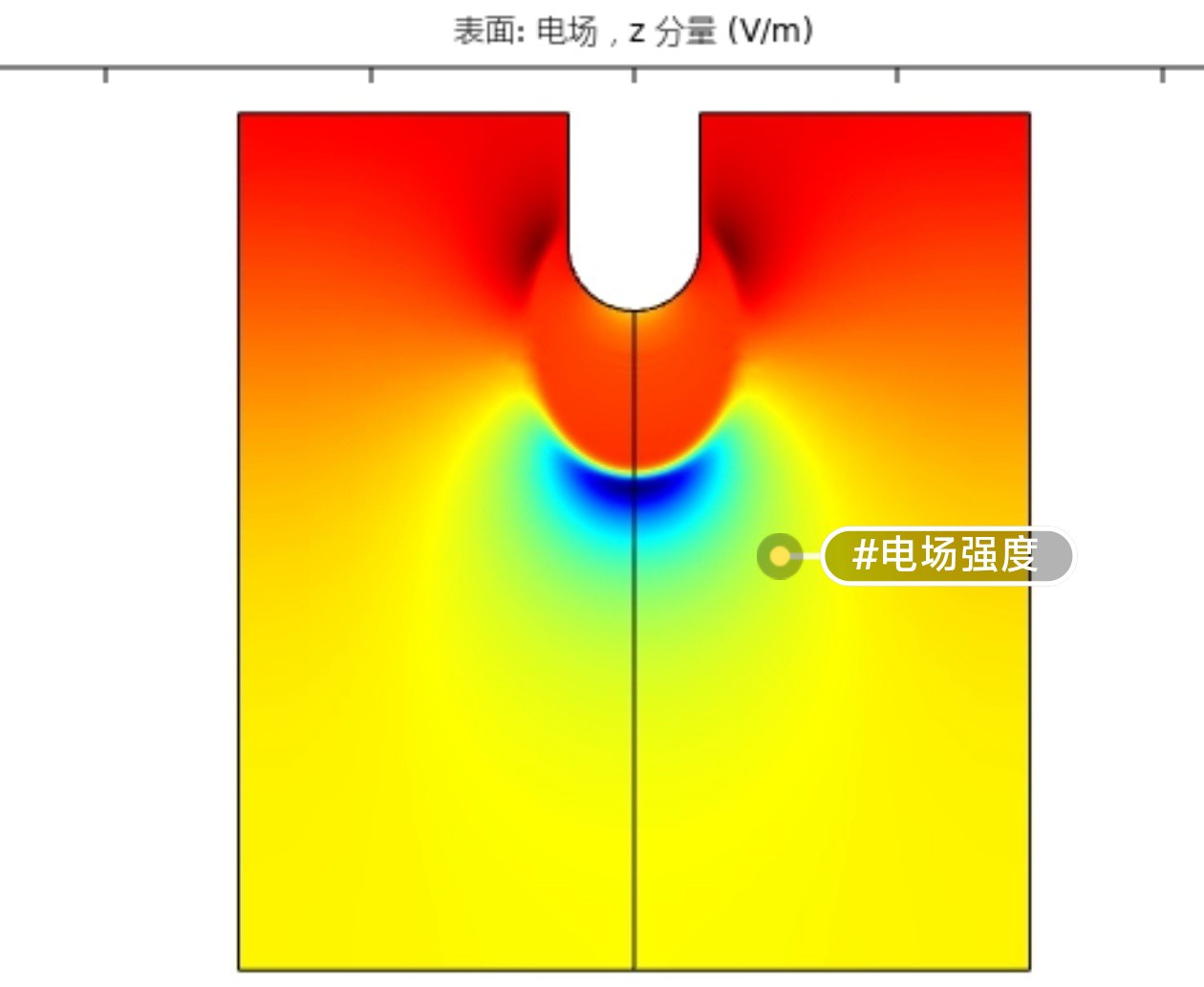
在流注放电的仿真中，棒板电极是一种常见的电极结构。棒板电极由一根金属棒和一块金属板组成，它们之间施加高电压以产生强电场。当空气或其他气体在强电场作用下发生电离时，就会形成空气流注。通过COMSOL等仿真工具，我们可以模拟这一过程，并观察和分析电场、电流和电荷的分布和变化。

四、等离子体仿真

在流注放电过程中，产生的等离子体具有许多独特的性质和应用。通过COMSOL等仿真工具，我们可以对等离子体的行为进行仿真和分析。例如，我们可以研究等离子体中的电子密度、离子密度、电导率等参数的变化，以及这些参数对流注放电过程的影响。此外，我们还可以通过仿真来探索等离子体在材料加工、环保、医疗等领域的应用。

五、结论

流注放电是一种重要的气体放电现象，涉及到许多复杂的物理过程和机制。通过使用COMSOL等仿真工具，我们可以更好地理解和分析流注放电过程和等离子体的行为。这不仅有助于我们更好地应对雷电、电器开关操作等实际问题，还有助于我们探索等离子体在材料加工、环保、医疗等领域的应用。未来，随着科技的发展和仿真技术的进步，我们将能够更深入地研究流注放电和等离子体行为，为人类的生产和生活带来更多的便利和价值。
流注放电，COMSOL放电仿真，等离子体仿真，棒板电极，空气流注，流注放电，需要拿去参考。