numpy小结

NumPy是Numerical Python的缩写。numerical ：relating to numbers; expressed in numbers

初识numpy——列表/元组转为数组

import numpy as np

list_demo = [1, 2, 3, 4]
a = np.array(list_demo)
print(a)

tuple_demo = ('1', '2', '3', '4')
b = np.asarray(tuple_demo)
print(b)

list_tuple = [('胡桃', '可莉', '纳西妲'), ('7.15', '7.27', '10.27')]
c = np.asarray(list_tuple)
print(c)

输出

[1 2 3 4]
['1' '2' '3' '4']
[['胡桃' '可莉' '纳西妲']
 ['7.15' '7.27' '10.27']]

第三个的输出：将列表转换为NumPy数组时，NumPy会将列表中的元组视为一个整体，并将该整体作为数组的一个元素。

初识numpy——创建数值数组

array1 = np.arange(0, 10, 2, int)
print(array1)

array2 = np.arange(0, 1, 0.2, float)
print(array2)

array3 = np.linspace(0, 1, num=5, endpoint=False, retstep=True)
print(array3)

输出

[0 2 4 6 8]
[0.  0.2 0.4 0.6 0.8]
(array([0. , 0.2, 0.4, 0.6, 0.8]), 0.2)

函数arange用于创建一个等差数列的一维数组，参数包括起始值、结束值（不包含在数组中）、步长和数据类型，其中起始值默认0，步长默认为1，数据类型参数可省略。

函数linspace用于在一定范围内生成等间隔的数值序列，其中参数num表示生成数组的元素个数，endpoint表示是否包含结束点，retstep表示是否返回步长。

其他方法：

ones(shape,dtype)：指定数组的形状，生成一个包含全1元素的数组。数据类型为dtype，可省略。

eye(N)：指定方阵的大小N，生成一个单位矩阵。

zeros(shape,dtype)：指定数组的形状，生成一个包含全0元素的数组。数据类型为dtype，可省略。

注：dtype可省略，shape可以只有一个，默认为行数。

比如

print(np.eye(2))
print(np.ones((3, 2)))
print(np.zeros((3, 2)))

输出

[[1. 0.]
 [0. 1.]]
[[1. 1.]
 [1. 1.]
 [1. 1.]]
[[0. 0.]
 [0. 0.]
 [0. 0.]]

注意到这里的ones与zeros都是用的((a,b))，不要只打一个括号。

事实上有eye(N, M=None, k=0, dtype=float)，这个比较复杂，单独说。它创建一个大小为(N, M)的二维数组，其中“对角线”上的元素为1，其他元素为0。偏移量k表示“对角线”向右的偏移量。比如：

e = np.eye(5, 6, -1, int)
print(e)

输出

[[0 0 0 0 0 0]
 [1 0 0 0 0 0]
 [0 1 0 0 0 0]
 [0 0 1 0 0 0]
 [0 0 0 1 0 0]]

-1表示向左偏移1。

Ndarray对象

Ndarray对象是NumPy库中的多维数组对象，集合了N个类型相同的数据，shape与dtype分别反应了数组维度与数据类型情况。创建Ndarray可以用array()方法，上文已经使用过了。原来是嵌套格式的序列会被转换成多维数组。

对Ndarray对象使用.ndim与.dtype可以获取数组维度数与数据类型，用.shape与.size可以获取大小(行,列)与元素数量，用. itemsize可以获取元素的字节数。

从外向里依次“剥皮”，也就是去掉[]，就分别是数组的第1,2,3,......维度，对应的是shape[0],shape[1],shape[2]…。而shape[n]的值的计算方法是：去掉外面的中括号之后，内部的最大的中括号有几个。

比如下文中去掉最外面的[]后，得到的单位体的个数表示第0个维度(axis=0)的大小，剩下的是[[1, 2, 3, 4],[1, 2, 3, 4],[1, 2, 3, 4]]，只有一个括号，所以shape[0]为1。

接着去掉[]后，剩下[1, 2, 3, 4],[1, 2, 3, 4],[1, 2, 3, 4]，有三个括号，所以shape[1]为3。

然后内部元素是4个，shape[2]为4。

list_demo = [[[1, 2, 3, 4],[1, 2, 3, 4],[1, 2, 3, 4]]]
a = np.array(list_demo)
print(a.ndim)
print(a.dtype)
print(a.shape)

输出

3
int32
(1, 3, 4)

上文提及了参数axis，该参数在sum求和里比较重要：

print(a.sum(axis=0))
print(a.sum(axis=1))
print(a.sum(axis=2))

输出

[[1 2 3 4]
 [1 2 3 4]
 [1 2 3 4]]
[[ 3  6  9 12]]
[[10 10 10]]

其中axis=0说明去掉一个[]，这时候shape[0]=1，此时就是一个数组，sum运算后还是该数组。axis=1说明去掉两层[]，这时候shape[1]=3，此时就是三个数组[1,2,3,4]，将这三个数组相加得到sum。axis=2说明去掉三层[]，这时候shape[2]=4，将1,2,3,4相加就是10。

现在应该大致明白了计算方法，下面来谈谈这个输出里面的[]个数如何确定。因为shape[0]=1的时候不方便观察和(因为axis==0时没有相加过程)，所以这里取shape[0]=2的一个数组，比如shape=(2,4,3)。比如

arr = [[[5, 0, 3], [3, 7, 3], [5, 2, 4], [7, 6, 8]], [[8, 1, 6], [7, 7, 8], [1, 5, 8], [4, 3, 0]]]
arr = np.asarray(arr)
print(arr, end='\n\n')
print(arr.sum(axis=0), end='\n\n')
print(arr.sum(axis=1), end='\n\n')
print(arr.sum(axis=2), end='\n\n')

输出

[[[5 0 3]
  [3 7 3]
  [5 2 4]
  [7 6 8]]

 [[8 1 6]
  [7 7 8]
  [1 5 8]
  [4 3 0]]]

[[13  1  9]
 [10 14 11]
 [ 6  7 12]
 [11  9  8]]

[[20 15 18]
 [20 16 22]]

[[ 8 13 11 21]
 [15 22 14  7]]

axis=0时，去掉最外层的[]，此时两个[[…]]的数组相加。

axis=1时，去掉中间的[]，此时[[[…]]]变为[[…]](但这与axis=0的时候的[[…]]是不一样的，因为去掉的那个[]不一样)。

axis-2时，去掉最内层的[]，此时是数字元素之间的相加了。

显式转换

arr = [[0.0, 1.0, 1.1], [-1.5, 1.5, -1.6]]
arr = np.array(arr)
print(arr)
print(arr.astype(np.int32))
输出
[[ 0.   1.   1.1]
 [-1.5  1.5 -1.6]]
[[ 0  1  1]
 [-1  1 -1]]

这里类型转化的时候的小数点是被截断的。

数组的操作

NumPy数组与普通的列表的操作差不多，这里仅说明一些比较重要的。

使用切片修改原数据

arr = [1, 2, 3, 4, 5]
arr = np.array(arr)
arr_slice = arr[2:4]  # 截取的是元素3,4
arr_slice[1] = 44  # 把截取的元素中的第二个(这里是4)改为44
print(arr)
输出[ 1  2  3 44  5]

如果想要arr_slice里的元素全部更改，可以用arr_slice[:]=44，不要忘记:了。

多维下标索引

和C里面的基本一样，比如

arr = [[1, 2, 3], [4, 5, 6]]
arr = np.array(arr)
print(arr[0], end='\t')
print(arr[0][1], end='\t')
print(arr[0, 1])
输出[1 2 3]	2	2

但是，如果需要的是某一部分的元素，难度比较大，需要索引与切片结合。比如

print(arr[:1, 2:])
输出[[3]]

这里输出的是行为:1，列为2:的元素。切片:1表示结束位置为1且不包括1，2:表示起始位置为2且包括2。又如

print(arr[1:, 1:2])
print(arr[:, 1:])

输出

[[5]]
[[2 3]
 [5 6]]

亦可对切片赋值：

arr[:, 1:] = 0
print(arr)
输出
[[1 0 0]
[4 0 0]]

转置

arr = [[1, 2, 3], [4, 5, 6]]
arr = np.array(arr)
print(arr.T)
print(arr.transpose())

输出均为

[[1 4]
 [2 5]
 [3 6]]

arr = np.arange(32).reshape((2, 4, 4))
print(arr)
print(arr.shape)
print(arr.transpose(1, 0, 2))
print(arr.transpose(1, 0, 2).shape)

输出

[[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]
  [12 13 14 15]]

 [[16 17 18 19]
  [20 21 22 23]
  [24 25 26 27]
  [28 29 30 31]]]
(2, 4, 4)
[[[ 0  1  2  3]
  [16 17 18 19]]

 [[ 4  5  6  7]
  [20 21 22 23]]

 [[ 8  9 10 11]
  [24 25 26 27]]

 [[12 13 14 15]
  [28 29 30 31]]]
(4, 2, 4)

这里(1,0,2)表示第一个维度(0)与第二个维度(1)交换，第三个维度(2)不变。也就是shape从(2,4,4)变为(4,2,4)。之前axis=0的维度里0123后面的是16171819，所以现在axis=1的维度里0123后面的是16171819，以此类推。

生成随机数组

print(np.random.randn(3,4))
print(np.random.choice([10,20,30]))
print(np.random.beta(1,5,10))

np.random.randn函数生成的是服从标准正态分布N~(0,1)的随机数。

np.random.choice从给的的数组里随机选一个元素。

np.random.beta是一个使用beta分布生成随机数的函数。前两个参数是beta分布的形状参数，第三个参数表示生成的随机数的数量。

Beta分布是一种连续型概率密度分布，表示为x~Beta(a,b)，由两个参数决定，称为形状参数。由于其定义域为(0,1)，一般被用于建模伯努利试验事件成功的概率的概率分布：为了测试系统的成功概率，我们做n次试验，统计成功的次数k，于是很直观地就可以计算出。然而由于系统成功的概率是未知的，这个公式计算出的只是系统成功概率的最佳估计。也就是说实际上也可能为其它的值，只是为其它的值的概率较小。因此我们并不能完全确定硬币出现正面的概率就是该值，所以也是一个随机变量，它符合Beta分布，其取值范围为0到1。

print(np.random.rand(2,4))
print(np.random.rand())
print(np.random.randint(1,10,3))

np.random.rand生成0~1的随机数

np.random.randint(1,10,3)生成1~10之间的长度为3的随机整数数组

np.array()和np.asarray()的区别

import numpy as np

arr1 = np.ones((3, 3))
arr2 = np.array(arr1)
arr3 = np.asarray(arr1)
arr1[1] = 2
print('arr1:\n', arr1)
print('arr2:\n', arr2)
print('arr3:\n', arr3)

输出

arr1:
 [[1. 1. 1.]
 [2. 2. 2.]
 [1. 1. 1.]]
arr2:
 [[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
arr3:
 [[1. 1. 1.]
 [2. 2. 2.]
 [1. 1. 1.]]

发现arr3被arr1改了，这是因为：

np.array(默认情况下)将会copy该对象，而np.asarray 除非必要，否则不会copy该对象。(必要的意思是数据源是ndarray类型时，不会copy)。也就是说array和asarray都可以将结构数据转化为ndarray，但是主要区别就是当数据源是ndarray时，array仍然会copy出一个副本，占用新的内存，但asarray不会。

矩阵的乘法——星乘*与点乘dot：

1.星乘*

①同型矩阵(哈达玛积)。对应位置的元素相乘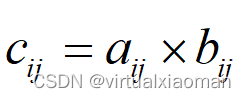

，如：

 

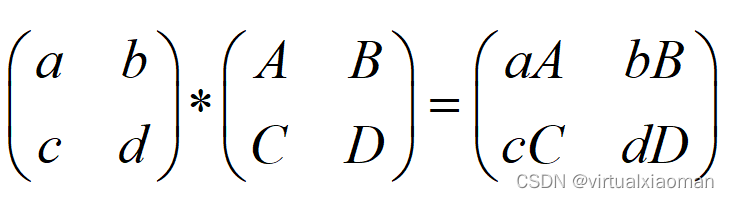
②不同型，但两个矩阵行数相等，其中一个矩阵列数为1。单列矩阵的列与另一个矩阵的列分别相乘：

如

 

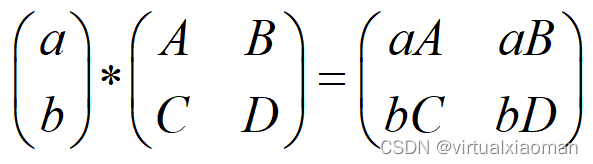
2.点乘dot

就是线代里的矩阵乘法

比如，

import numpy as np

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
c = np.array([[1], [2]])
print(a * b, '\n')
print(c * b, '\n')
print(b * c, '\n')
print(np.dot(a, b))

输出

[[ 5 12]
 [21 32]] 

[[ 5  6]
 [14 16]] 

[[ 5  6]
 [14 16]] 

[[19 22]
 [43 50]]

矩阵的逆矩阵：

与线代的定义一样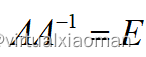，，比如：

import numpy as np

a = np.array([[1, 2], [3, 4]])
a_inv = np.linalg.inv(a)
print(a_inv)
print(np.dot(a, a_inv))

 输出

[[-2.   1. ]
 [ 1.5 -0.5]]
[[1.0000000e+00 0.0000000e+00]
 [8.8817842e-16 1.0000000e+00]]

inv是inverse的缩写：相反的，倒转的；颠倒的，逆的

linalg是numpy库中的线性代数模块，可以用于进行矩阵和向量的运算，linalg是linear algebra(线性代数)的缩写。

这里有烦人的浮点数，可以这样修改代码：

a_dot_a_inv = np.dot(a, a_inv)
a_dot_a_inv = np.round(a_dot_a_inv).astype(int)  # 将a_dot_a_inv中的元素四舍五入为整数
print(a_dot_a_inv)

输出

[[1 0]
 [0 1]]