数据结构与算法分析 1-引论

一、数学知识

1.对数

 2.级数

 

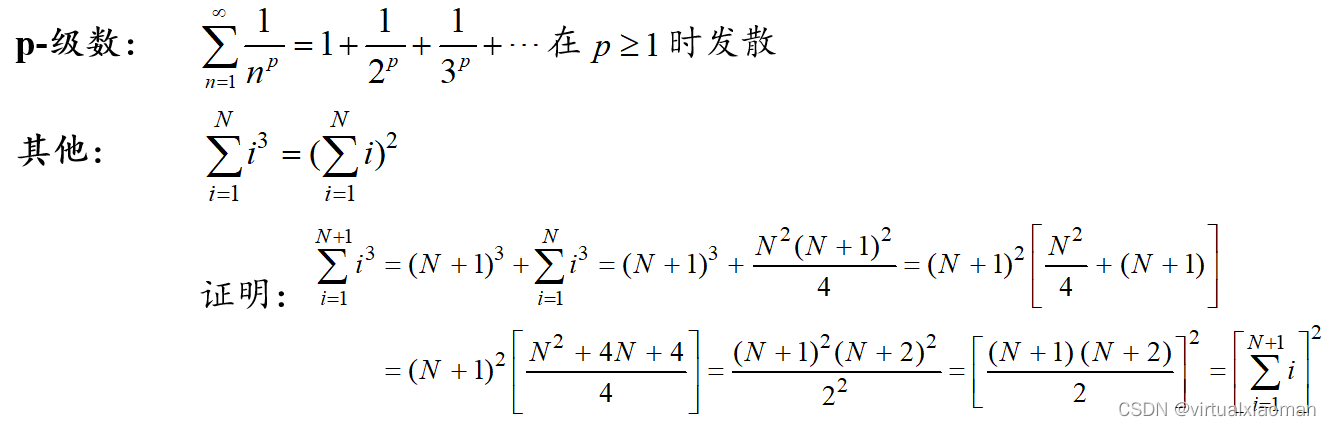
3.模运算

 

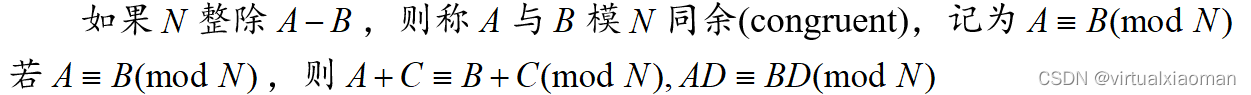
4.证明方法

①归纳法

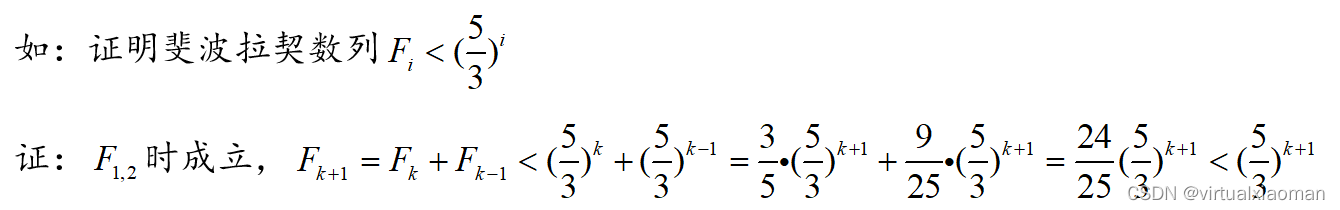
②反证法 

 

二、递归

1.定义

当一个函数用它自己来定义时就成为是递归的(recursive)

2.基本准则

①基准情形base case：必须有某些基准的情形，它们不用递归就能求解。

②不断推进making progress：递归调用必须能够朝着产生基准情形的方向推进。

③设计法则design rule：所有的递归调用都能运行。

④合成效益法则compound interest rule：在求解一个问题的同一实例时，切勿在不同的递归调用中做重复性工作。

3.递归实例

①数学表达式

#include <stdio.h>
int F(int X)
{
	if (X == 0)
		return 0;
	else
		return 2 * F(X - 1) + X * X;
}
int main()
{
	printf("%d", F(3));
}

 递归实际上就类似于数学里的函数表达式，比如这里就是

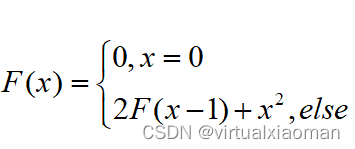
②打印输出数

#include <stdio.h>
void PrintDigit(int N)
{
	printf("%d", N);
}
void PrintOut(unsigned int N)
{
	if (N >= 10)
		PrintOut(N / 10);
	PrintDigit(N % 10);
}
int main()
{
	PrintOut(3234);
}

这里假装PrintDigit只能输出一个数字。这里通过递归实现输出多位数。