虽然有回归两个字,但是依然是解决的时分类问题,是最经典的二分类算法。
分类算法有很多,例如支持向量机和神经网络。而逻辑回归算法应用的比较广,往往是优先选择的算法。
Sigmod函数
表达式:
g(z)=11+e−z
g(z)=\frac{1}{1+e^{-z}}
g(z)=1+e−z1
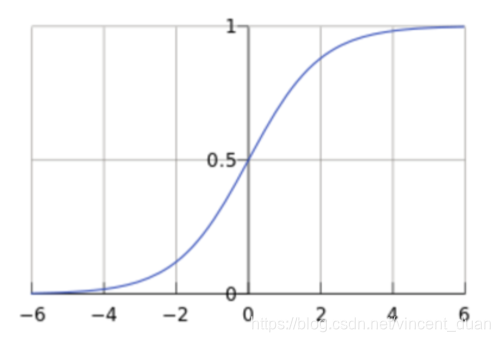
自变量取值为任意实数,值域[0,1]
在线性回归中的结果预测出一个值,将这个值放到这个sigmod中,得到一个输出结果,而这个结果可以表示为概率值。
假设预测函数: hθ(x)=g(θTx)=11+e−θTxh_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}hθ(x)=g(θTx)=1+e−θTx1,
其中 θ0+θ1x+θ2x+,...,θnx=∑i=1nθixi=θTx\theta_0+\theta_1x+\theta_2x+,...,\theta_nx=\sum_{i=1}^n{\theta_ix_i}=\theta^Txθ0+θ1x+θ2x+,...,θnx=∑i=1nθixi=θTx
假设这是一个二分类任务:
{P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)
\begin{cases}
P(y=1|x;\theta)=h_\theta(x) \\
P(y=0|x;\theta)=1-h_\theta(x)
\end{cases}
{P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)
可以将上面的公式进行整合:
P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
P(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}
P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
上面的公式对于二分类任务(0,1),整合后y取0只保留(1−hθ(x))1−y(1-h_\theta(x))^{1-y}(1−hθ(x))1−y,y取1只保留(hθ(x))y(h_\theta(x))^y(hθ(x))y
逻辑回归似然函数
L(θ)=∏i=1mP(yi∣xi;θ)=∏i=1m(hθ(xi)yi(1−hθ(xi))1−yi)
L(\theta)=\prod_{i=1}^mP(y_i|x_i;\theta)=\prod_{i=1}^m(h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{1-y_i})
L(θ)=i=1∏mP(yi∣xi;θ)=i=1∏m(hθ(xi)yi(1−hθ(xi))1−yi)
对数似然函数为:
l(θ)=logL(θ)=∑i=1m(yiloghθ(xi)+(1−y)log(1−hθ(xi)))
l(\theta)=logL(\theta)=\sum_{i=1}^m(y_ilogh_\theta(xi)+(1-y)log(1-h_\theta(xi)))
l(θ)=logL(θ)=i=1∑m(yiloghθ(xi)+(1−y)log(1−hθ(xi)))
而似然函数是要求一个最大值,此时应用梯度上升求最大值,但是一般通过引入J(θ)=−1ml(θ)J(\theta)=-\frac{1}{m}l(\theta)J(θ)=−m1l(θ)转换为梯度下降任务。
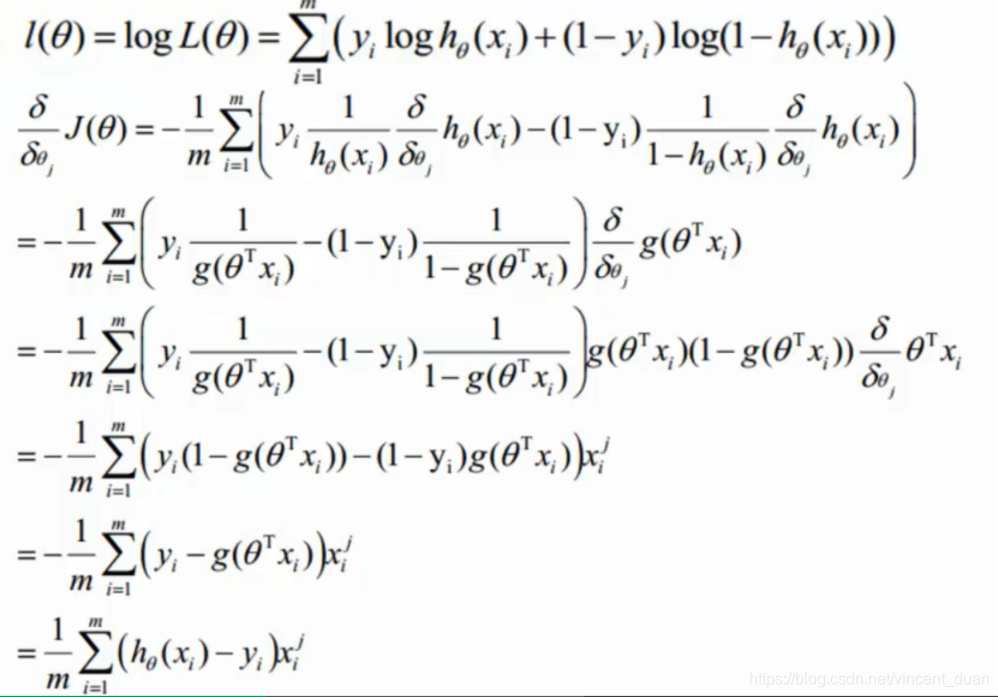
其中θj\theta_jθj表示第jjj个特征。最终结果为1m∑i=1m(hθ(xi)−yi)xij\frac{1}{m}\sum_{i=1}^m(h_\theta(x_i)-y_i)x_i^jm1∑i=1m(hθ(xi)−yi)xij
其中xijx_i^jxij表示第iii个样本第jjj个特征。
更新参数θj\theta_jθj
θj:=θj−α1m∑i=1m(hθ(xi)−yi)xij
\theta_j :=\theta_j -\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x_i)-y_i)x_i^j
θj:=θj−αm1i=1∑m(hθ(xi)−yi)xij
其中α\alphaα表示步长,∑i=1m(hθ(xi)−yi)xij\sum_{i=1}^m(h_\theta(x_i)-y_i)x_i^j∑i=1m(hθ(xi)−yi)xij表示方向,1m\frac{1}{m}m1表示综合考虑每一个样本。
多分类softmax
上面都是基于二分类的逻辑回归,而对于一个多分类问题,往往使用softmax算法,公式如下:
hθ(x(i))=[p(y(i)=1∣x(i);θ)p(y(i)=2∣x(i);θ)⋮p(y(i)=k∣x(i);θ)]=1∑j=1keθjTx(i)[eθ1Tx(i)eθ2Tx(i)⋮eθkTx(i)]
h_\theta(x^{(i)})=\begin{bmatrix}
p(y^{(i)}=1|x^{(i)};\theta) \\
p(y^{(i)}=2|x^{(i)};\theta) \\
\vdots \\
p(y^{(i)}=k|x^{(i)};\theta)
\end{bmatrix}=\frac{1}{\sum_{j=1}^ke^{\theta^T_jx^{(i)}}}\begin{bmatrix}
e^{\theta^T_1x^{(i)}} \\
e^{\theta^T_2x^{(i)}} \\
\vdots \\
e^{\theta^T_kx^{(i)}}
\end{bmatrix}
hθ(x(i))=⎣⎢⎢⎢⎡p(y(i)=1∣x(i);θ)p(y(i)=2∣x(i);θ)⋮p(y(i)=k∣x(i);θ)⎦⎥⎥⎥⎤=∑j=1keθjTx(i)1⎣⎢⎢⎢⎢⎡eθ1Tx(i)eθ2Tx(i)⋮eθkTx(i)⎦⎥⎥⎥⎥⎤
python实现最简单的逻辑回归
我们将建立一个逻辑回归模型来预测一个学生是否被大学录取。假设你是一个大学系的管理员,你想根据两次考试的结果来决定每个申请人的录取机会。你有以前的申请人的历史数据,你可以用它作为逻辑回归的训练集。对于每一个培训例子,你有两个考试的申请人的分数和录取决定。为了做到这一点,我们将建立一个分类模型,根据考试成绩估计入学概率。
数据
34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
1.1 引入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
查看数据情况:
positive=pdData[pdData['Admitted']==1]
negative=pdData[pdData['Admitted']==0]
fig,ax=plt.subplots(figsize=(10,5))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=30, c='b', marker='o',label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=30, c='r', marker='x',label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 score')
ax.set_ylabel('Exam 2 score')
输出结果如下:
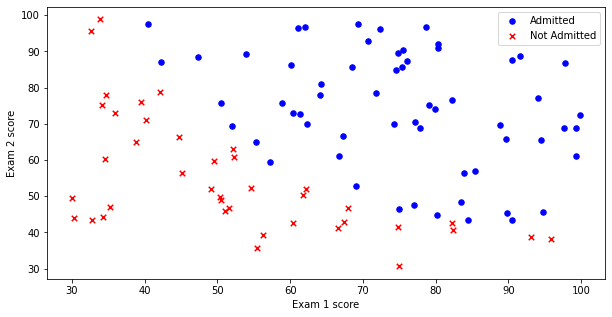
2要完成的模块
- sigmod:映射到概率的函数
- model:返回预测结果值
- cost:计算参数损失
- gradient:计算每个参数的梯度方向
- descent:进行参数更新
- accuracy:计算精度
2.1目标
建立分类器,求解出三个参数θ0,θ1,θ2\theta_0,\theta_1,\theta_2θ0,θ1,θ2,其中θ1\theta_1θ1对应第一个考试成绩,θ2\theta_2θ2对应第二个考试成绩,θ0\theta_0θ0对应偏置项。
设置阈值,根据阈值判断录取结果。
2.2 sigmod函数
def sigmod(z):
return 1/(1+np.exp(-1))
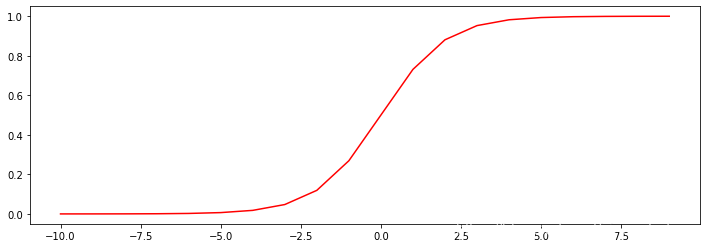
举例展示:
nums = np.arange(-10, 10, step=1)
fig,ax=plt.subplots(figsize=(12, 4))
ax.plot(nums,sigmod(nums),'r')
2.3 model
def model(X, theta):
return sigmod(np.dot(X, theta.T)) # 进行矩阵乘法
(θ0,θ1,θ2)×[1x1x2]=θ0+θ1x1+θ2x2
(\theta_0, \theta_1, \theta_2) \times \begin{bmatrix}
1 \\
x_1 \\
x_2
\end{bmatrix}=\theta_0 + \theta_1x_1 + \theta_2x_2
(θ0,θ1,θ2)×⎣⎡1x1x2⎦⎤=θ0+θ1x1+θ2x2
构造初始化数据:
pdData.insert(0, 'Ones', 1) # 添加列,列名Ones,数据全为1
orig_data = pdData.values # 将DataFrame转为矩阵
cols = orig_data.shape[1] #获取列数量 4
X = orig_data[:,0:cols-1] # 获取第一列、第二列、第三列数据
y = orig_data[:,cols-1:cols] #获取第四列数据
theta = np.zeros([1,3]) # 创建1行3列的零矩阵
查看数据X:
查看标签y:

查看参数θ\thetaθ:

查看shape:

2.4 损失函数
将上面所讲的对数似然函数取负号,因为要转为梯度下降:
D(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
D(h_\theta(x),y) = -ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))
D(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
求平均损失:
J(θ)=1n∑i=1nD(hθ(xi),yi)
J(\theta) = \frac{1}{n}\sum_{i=1}^nD(h_\theta(x_i),y_i)
J(θ)=n1i=1∑nD(hθ(xi),yi)
def cost(X,y,theta):
left=np.multiply(-y, np.log(model(X,theta)))
right=np.multiply(1-y,np.log(1-model(X,theta)))
return np.sum(left - right)/(len(X))
运行损失函数:
cost(X,y,theta)
结果如下:
0.6931471805599453
2.5 计算梯度
根据上面得出的偏导公式:
∂J∂θj=1m∑i=1n(hθ(xi)−yi)xij
\frac {\partial J}{\partial \theta_j}=\frac{1}{m}\sum_{i=1}^n(h_\theta(x_i)-y_i)x_i^j
∂θj∂J=m1i=1∑n(hθ(xi)−yi)xij
m表示样本个数,n表示参数θ\thetaθ个数
def gradient(X,y,theta):
grad = np.zeros(theta.shape) # 当前有三个参数,因此有三个梯度,梯度与theta一一对应
error = (model(X,theta) - y).ravel() # 将负号提到里面
for j in range(len(theta.ravel())): # 3个参数,求三次偏导
term = np.multiply(error, X[:,j])
grad[0,j] = np.sum(term)/len(X)
return grad
这样就获取到三个特征的梯度。
3 批量梯度下降GD、随机梯度下降SGD、小批量梯度下降的各自表现
STOP_ITER=0 # 迭代次数,按照迭代次数停止,
STOP_COST=1 # 损失变化,可以看迭代前的目标函数,和迭代后的目标函数,如果这两次迭代生成的目标函数差异非常小,就可以停止
STOP_GRAD=2 # 梯度变化,梯度如果变化很小,那么可以停止
def stopCriterion(type, value, threshold):
# 设定三种不同的停止策略
if type == STOP_ITER: return value > threshold
elif type == STOP_COST: return abs(value[-1]-value[-2]) < threshold
elif type == STOP_GRAD: return np.linalg.norm(value) < threshold
3.1 数据洗牌
防止数据有一定的规律,让模型的泛化能力能强,对数据进行洗牌,
import numpy.random
#洗牌
def shuffleData(data):
np.random.shuffle(data)
cols = data.shape[1]
X = data[:, 0:cols-1]
y = data[:, cols-1:]
return X,y
3.2 梯度下降
import time
def descent(data, theta, batchSize, stopType, thresh, alpha):
# data:数据
# theta: 参数
# batchSize=1 表示随机梯度下降,batchSize=总样本数 表示梯度下降,batchSize=(1到总体之间)表示小批量梯度下降
# stopType表示停止策略
# thresh表示停止策略对应的阈值
# alpha表示学习率
# 初始化
init_time = time.time()
i = 0 # 迭代次数
k = 0 # batch
X, y = shuffleData(data)
grad = np.zeros(theta.shape) # 梯度
costs = [cost(X, y, theta)] # 损失值
while True:
grad = gradient(X[k:k+batchSize], y[k:k+batchSize], theta)
k += batchSize # 取batch数量个数据
if k >= n:
k = 0
X, y = shuffleData(data) # 重新洗牌
theta = theta-alpha*grad #更新参数
costs.append(cost(X, y, theta)) # 重新计算新的损失
i += 1
if stopType == STOP_ITER: value = i
elif stopType == STOP_COST: value = costs
elif stopType == STOP_GRAD: value = grad
if stopCriterion(stopType, value, thresh): break
return theta, i-1, costs, grad, time.time() - init_time
3.3 执行梯度下降函数
def runExpe(data, theta, batchSize, stopType, thresh, alpha):
#import pdb; pdb.set_trace();
theta, iter, costs, grad, dur = descent(data, theta, batchSize, stopType, thresh, alpha)
name = "Original" if (data[:,1]>2).sum() > 1 else "Scaled"
name += " data - learning rate: {} - ".format(alpha)
if batchSize==n: strDescType = "Gradient"
elif batchSize==1: strDescType = "Stochastic"
else: strDescType = "Mini-batch ({})".format(batchSize)
name += strDescType + " descent - Stop: "
if stopType == STOP_ITER: strStop = "{} iterations".format(thresh)
elif stopType == STOP_COST: strStop = "costs change < {}".format(thresh)
else: strStop = "gradient norm < {}".format(thresh)
name += strStop
print ("***{}\nTheta: {} - Iter: {} - Last cost: {:03.2f} - Duration: {:03.2f}s".format(name, theta, iter, costs[-1], dur))
fig, ax = plt.subplots(figsize=(12,4))
ax.plot(np.arange(len(costs)), costs, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title(name.upper() + ' - Error vs. Iteration')
return theta
3.3.1 批量梯度下降GD
3.3.1.1 根据迭代次数进行停止
runExpe(orig_data, theta, 100, STOP_ITER, thresh=5000, alpha = 0.000001)
按照迭代次数进行停止,迭代5000次,学习率是 0.000001
运行结果:
***Original data - learning rate: 1e-06 - Gradient descent - Stop: 5000 iterations
Theta: [[-0.00027127 0.00705232 0.00376711]] - Iter: 5000 - Last cost: 0.63 - Duration: 0.77s
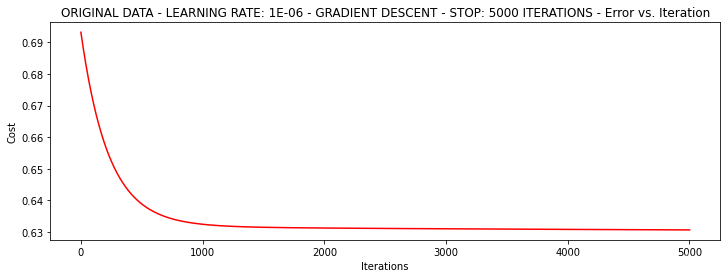
其中x轴是迭代次数,y轴是损失值,随着迭代次数的增加,目标函数逐渐收敛。
当前的时间消耗0.77s。
3.3.1.2 根据损失函数变化进行停止
runExpe(orig_data, theta, 100, STOP_COST, thresh=0.000001, alpha = 0.001)
设置阈值1E-6,差不多需要迭代110000次。
输出结果如下:
***Original data - learning rate: 0.001 - Gradient descent - Stop: costs change < 1e-06
Theta: [[-5.13364014 0.04771429 0.04072397]] - Iter: 109901 - Last cost: 0.38 - Duration: 17.36s
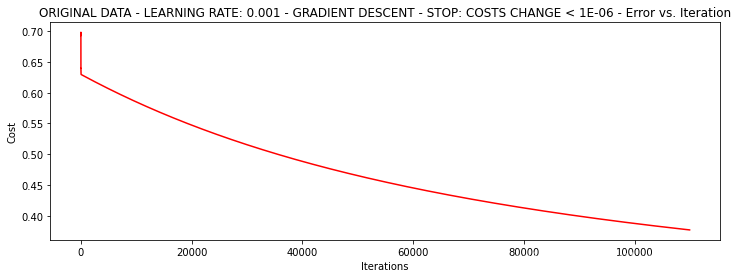
可以看出时间花了17.36s
3.3.1.3 根据梯度值进行停止
runExpe(orig_data, theta, 100, STOP_GRAD, thresh=0.05, alpha = 0.001)
输出结果如下:
***Original data - learning rate: 0.001 - Gradient descent - Stop: gradient norm < 0.05
Theta: [[-2.37033409 0.02721692 0.01899456]] - Iter: 40045 - Last cost: 0.49 - Duration: 6.67s

根据第一张图,看似迭代5000次就已经到达瓶颈了,其实如果迭代11万次依然可以达到一个很高的准确率,所以不要被一张图蒙蔽了。
3.3.2 随机梯度下降SGD
每次只迭代一个样本
3.3.2.1 根据迭代次数进行停止
runExpe(orig_data, theta, 1, STOP_ITER, thresh=5000, alpha = 0.001)
这里的学习率是0.001,根本不能收敛
输出结果如下:
***Original data - learning rate: 0.001 - Stochastic descent - Stop: 5000 iterations
Theta: [[-0.38304524 0.02692472 0.07197214]] - Iter: 5000 - Last cost: 1.98 - Duration: 0.27s
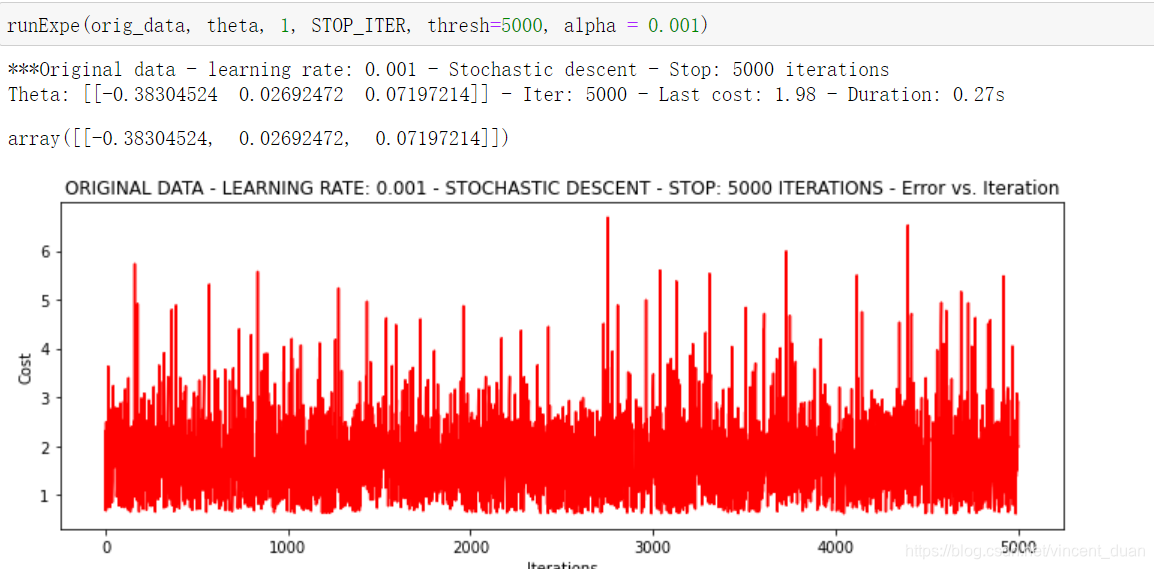
而当我们的学习率改为0.000001后,输出结果如下:
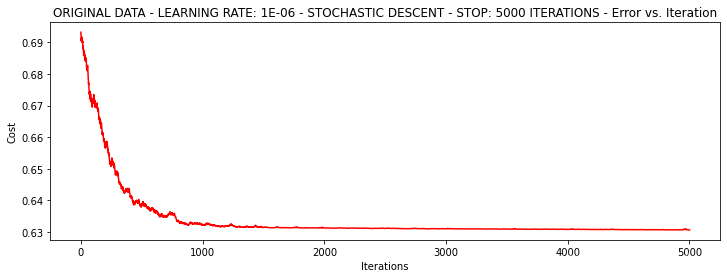
3.3.3 小批量梯度下降
每次只迭代一批样本
runExpe(orig_data, theta, 16, STOP_ITER, thresh=5000, alpha = 0.001)
输出结果如下:
***Original data - learning rate: 0.001 - Mini-batch (16) descent - Stop: 5000 iterations
Theta: [[-0.35752768 0.01835205 0.0004876 ]] - Iter: 5000 - Last cost: 0.61 - Duration: 0.35s
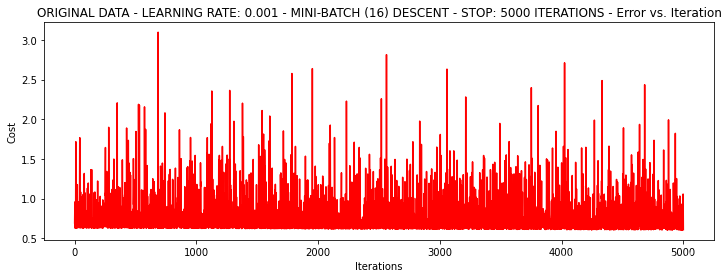
与上面的图像相似,同样可以通过修改学习率进行改善:

除了将学习率调小之外,还有其他方式来改善。
可以通过对数据进行标准化,将数据按其属性(按列进行)减去其均值,然后除以其方差。最后得到的结果是,对每个属性/每列来说所有数据都聚集在0附近,方差值为1。实现方式如下:
from sklearn import preprocessing as pp
scaled_data = orig_data.copy()
scaled_data[:, 1:3] = pp.scale(orig_data[:, 1:3])
runExpe(scaled_data, theta, n, STOP_ITER, thresh=5000, alpha = 0.001)
输出结果如下:
***Scaled data - learning rate: 0.001 - Gradient descent - Stop: 5000 iterations
Theta: [[0.3080807 0.86494967 0.77367651]] - Iter: 5000 - Last cost: 0.38 - Duration: 0.86s
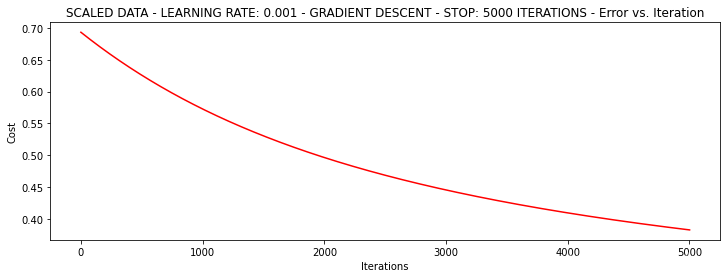
昨晚sklearning之后,变得收敛了。
4. 精度
def predict(X, theta):
return [1 if x >= 0.5 else 0 for x in model(X, theta)]
scaled_X = scaled_data[:, :3]
y = scaled_data[:, 3]
predictions = predict(scaled_X, theta)
correct = [1 if ((a==1 and b==1) or (a==0 and b==0)) else 0 for (a,b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print('accuracy = {0}%'.format(accuracy))





 这篇博客详细介绍了逻辑回归在解决二分类问题中的作用,包括 Sigmod 函数的使用、逻辑回归模型的构建、似然函数及对数似然函数的推导、梯度下降法的实现过程。通过实例展示了如何用 Python 实现逻辑回归,比较了批量梯度下降、随机梯度下降和小批量梯度下降在不同停止条件下的性能。此外,还讨论了数据预处理如标准化对模型收敛性的影响,并给出了模型的精度评估方法。
这篇博客详细介绍了逻辑回归在解决二分类问题中的作用,包括 Sigmod 函数的使用、逻辑回归模型的构建、似然函数及对数似然函数的推导、梯度下降法的实现过程。通过实例展示了如何用 Python 实现逻辑回归,比较了批量梯度下降、随机梯度下降和小批量梯度下降在不同停止条件下的性能。此外,还讨论了数据预处理如标准化对模型收敛性的影响,并给出了模型的精度评估方法。
















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








