PTA 08-图8 How Long Does It Take

最新推荐文章于 2022-05-20 16:28:34 发布

原创最新推荐文章于 2022-05-20 16:28:34 发布 · 245 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #拓扑学 #队列 #算法

陈越PTA训练专栏收录该内容

33 篇文章

订阅专栏

本文解析了一个关于项目管理中如何利用拓扑排序算法找到最早完成时间的编程问题。通过分析活动关系，计算节点的入度并运用队列实现EarliestTime计算，解决关键路径问题。关键点在于理解活动的起始点、结束点和持续时间，以及如何应用拓扑排序找出最早完成项目的方法。

PTA 08-图8 How Long Does It Take

原题链接
Given the relations of all the activities of a project, you are supposed to find the earliest completion time of the project.

Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of activity check points (hence it is assumed that the check points are numbered from 0 to N−1), and M, the number of activities. Then M lines follow, each gives the description of an activity. For the i-th activity, three non-negative numbers are given: S[i], E[i], and L[i], where S[i] is the index of the starting check point, E[i] of the ending check point, and L[i] the lasting time of the activity. The numbers in a line are separated by a space.

Output Specification:
For each test case, if the scheduling is possible, print in a line its earliest completion time; or simply output “Impossible”.

Sample Input 1:
9 12
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
5 4 0
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4
结尾无空行
Sample Output 1:
18
结尾无空行

Sample Input 2:
4 5
0 1 1
0 2 2
2 1 3
1 3 4
3 2 5
Sample Output 2:
Impossible

思路

本题是拓扑排序中的EarliestTime的问题
算法是根据陈越姥姥数据结构课写的：
1利用Indegree[]数组来存入度的大小
2利用了queue队列来存入度为0的结点
3利用cnt来计算这个出度的节点数，如果结点不是V，则构成回路
在这里插入图片描述
关键路径问题：

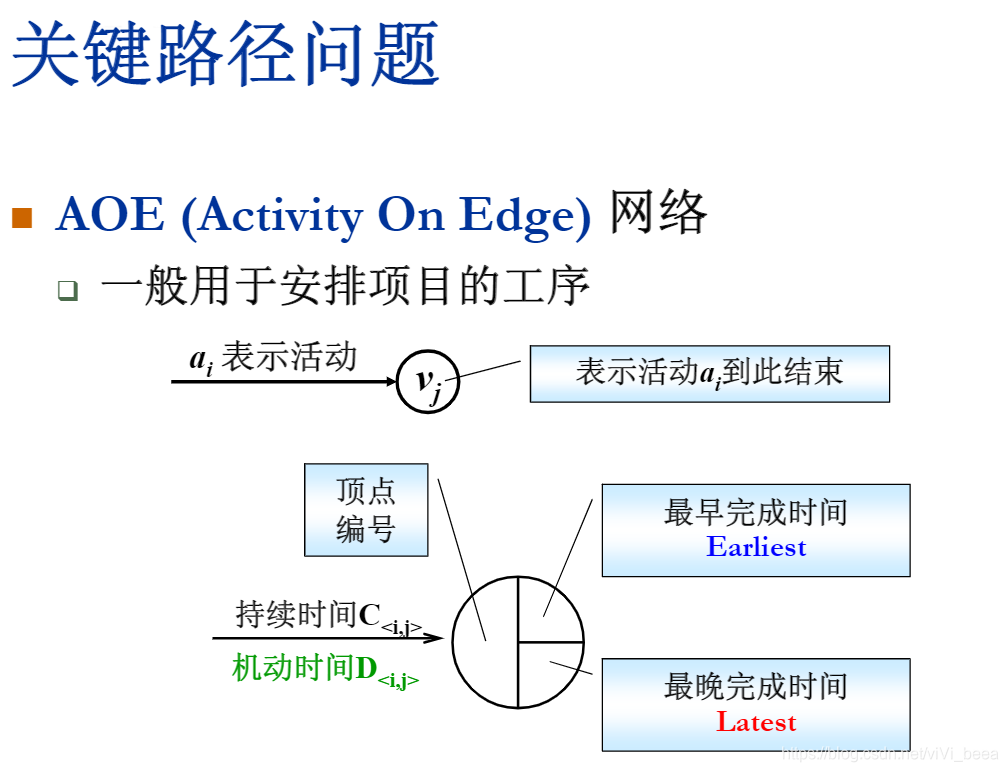
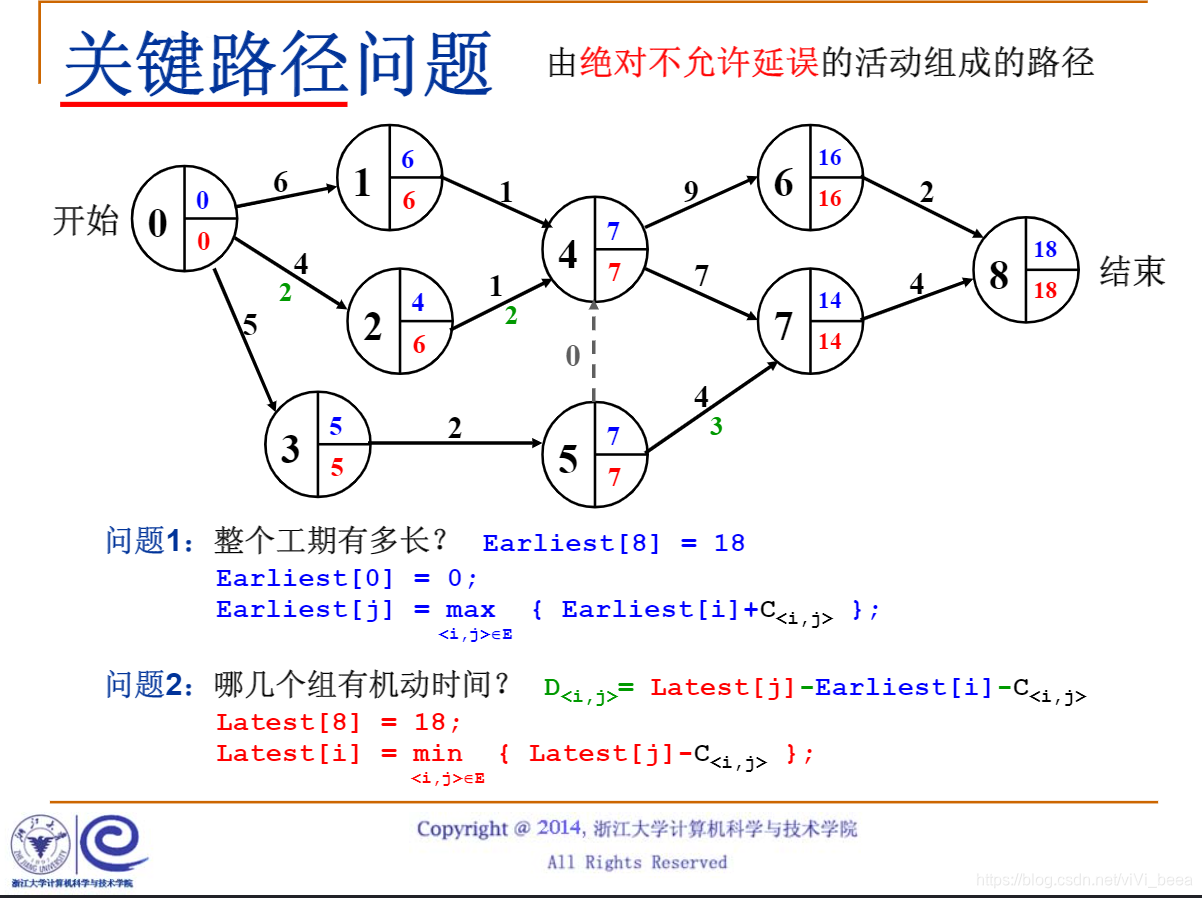
Earlieast[j]=max{Earliest[i]+C<i,j>}
最早动工的时间是前面一个结点+这个结点的工期的最大值，因为必须完成这个结点前的全部结点，才能开始这个结点的动工

Code

#include<iostream>
#include<queue>
#define MaxN 101
#define INIFITE 100001
using namespace std;
int G[MaxN][MaxN];//存拓扑
int Indegree[MaxN];//保存入度
int EarliestTime[MaxN];//存每个节点的最早完成值
int N,M;//N个顶点M条边

void Topsort(){
    for(int i=0;i<N;i++){
        for(int j=0;j<N;j++){
            if(G[i][j]!=INIFITE){
                Indegree[j]++;//计算入度的值
            }
        }
    }
    queue<int> q;
    int cnt=0;
    for(int i=0;i<N;i++){
        if(Indegree[i]==0){
            q.push(i);//将入度为0的元素入队
        }
    }
    while(!q.empty()){
        int v=q.front();
        q.pop();
        cnt++;
        for(int i=0;i<N;i++){
            if(G[v][i]!=INIFITE){
                if(EarliestTime[v]+G[v][i]>EarliestTime[i]){
                EarliestTime[i]=EarliestTime[v]+G[v][i];
                }
                if(--Indegree[i]==0){
                    q.push(i);
                }
            }
        }
    }
    if(cnt!=N){
        printf("Impossible");
    }else{
        int max=-1;
        for(int i=0;i<N;i++){
            if(max<EarliestTime[i]){
                max=EarliestTime[i];
            }
        }
        printf("%d",max);
    }
}

int main(){
    scanf("%d %d",&N,&M);
    for(int i=0;i<N;i++){
        Indegree[i]=0;//初始化入度
        EarliestTime[i]=0;//初始化最早完成时间
        for(int j=0;j<N;j++){
            G[i][j]=INIFITE;//初始化
        }
    }
    int i,j;
    for(int ii=0;ii<M;ii++){
        scanf("%d %d",&i,&j);
        scanf("%d",&G[i][j]);
    }
    Topsort();
    return 0;
}