离散数学代数部分

最新推荐文章于 2025-04-29 09:22:12 发布

nlp菜菜

最新推荐文章于 2025-04-29 09:22:12 发布

阅读量4.8k

点赞数 6

本文链接：https://blog.youkuaiyun.com/vegetable_me/article/details/106563295

版权

马上考试了又整理了一波…仓促之下有缺漏错误，望各位指正，感谢！

代数结构（代数系统/群环/格与布尔代数）和数论部分

基本概念

二元运算

二元运算 S×S→S：结果唯一且封闭（结果仍∈S）
- 性质
  - 交换律/结合律/幂等律/分配律
  - 吸收律：x◦(xy)=x,x(x◦y)=x
- 特异元素
  - 单位元/幺元e：既是左单位元元又是右单位元
    - 左单位元e*x=x
    - 右单位元x*e=x
  - 零元θ：既是左零元又是右零元
    - 左零元θ*x=θ
    - 右零元x*θ=θ
  - 逆元x^-1（左/右）
    - 左逆元yl*x=e
    - 右逆元x*yr=e
    - 可逆的元素：逆元存在，记作x^-1
      代数系统
代数系统V=<S, f1, f2, …, fk>：非空集合S+S上 k个一元或二元运算
- 代数常数：运算的特异元素（幺元/单位元）
- 同类型的代数系统：运算个数和元数相同，代数常数个数相同
- 子代数<B, f1, f2, …, fk>：B关于这些运算封闭，且和S有相同的代数常数
- 最小子代数：如果代数常数关于运算封闭，则它们共同组成最小子代数
- 最大子代数：V
- 平凡子代数：最小和最大子代数
- 真子代数：B是V的真子集
- 积代数：V₁=<A,◦>和V₂=<B,∗> 同类型，则V=V₁×V₂=<A×B,·>`是积代数
- 元素计算<a₁,b₁>▪<a₂,b₂>=<a₁◦a₂, b₁∗b₂>
- 因子代数：V₁，V₂
- 同态映射：满足f(x◦y)=f(x)*f(y)
- 单同态/满同态V₁∼V₂（同态像）/同构V₁≅V₂ 类似于函数中的单射/满射/双射
- 自同态：V₁=V₂
群
代数系统：运算封闭
半群：代数系统 + 运算可结合
独异点/含幺半群：半群+ 存在单位元
群：独异点 + 所有元素存在逆元
- Klein四元群{e,a,b,c}，a/b/c任意两个元素运算都等于剩下第三个元素，元素逆元是自己，满足交换律
- 有限群/无限群：G是有穷集/反之
- 阶*|G|*：G的基数
- 平凡群：只含单位元的群
- 交换群（Abel群）：二元运算可交换的群
- k阶元|a|=k：使得a^k=e成立的最小正整数k
- 无限阶元：不存在k
子群H：H关于G中运算构成群，H≤G
- 真子群：H⊂G ，记作H<G
- 平凡子群：G和{e}
- a生成的子群*< a >：< a >=H={a^k| k∈ Z}
- 中心C*：C是G的子群，C={a| a∈ G∧∀x∈ G(ax=xa)}
- 子群格：偏序集< L(G), ⊆ > ，且L(G) = {H | H是G的子群}
- 陪集
- 右陪集Ha：H是G的子群，a∈G(G中运算是*)，Ha={ha | h∈ H}
- 左陪集aH*
- 代表元素：a
- 等价关系[a]_R=Ha：∀a,b∈ G, <a,b>∈ R ⇔ ab^-1∈ H
- 正规子群/不变子群：∀a∈ G , Ha=aH
循环群G=< a >（一定是Abel群）：见前生成的子群，a是G的生成元
- n阶循环群：|G|=n,G = { a⁰=e, a¹, a², … , a^n-1 }
- 无限循环群：G = { a⁰=e, a^±1, a^±2, … }
n元置换
轮换与对换的转化：(i¹i² … i^k) = (i¹ i²) (i¹ i³) … (i¹ i^k)
- 奇置换：对换为奇数个，有n!/2个
n元对称群S_n：n元置换构成的集合S_n关于置换乘法构成群
- n元置换群：n元对称群的子群
- n元交错群A_n：S_n的子群，是所有的n元偶置换的集合
  环和域
环：<R,+,·>代数系统 + <R,+> 是交换群 + <R,·>构成半群 + ·运算关于+运算适合分配律
- 环中加法+，环中乘法·
- 负元-x：加法的逆元
- 单位元：加法单位元记作0，乘法单位元（如果存在）记作1
- 逆元x^-1：乘法逆元（不一定存在）
交换环：环中乘法 ·适合交换律
含幺环：环中乘法 ·存在单位元
无零因子环：任何元素只有和零元素相乘才能得到零元
整环：交换环+含幺环+无零因子环
域：整环+ 元素>=2 + 除0之外的元素都有逆元
格
格/偏序格：设<S, ≼>是偏序集，如果所有x,y∈S，{x,y}都有最小上界和最大下界，则称S关于偏序≼作成一个格（偏序格）
- 求最小上界：x∨y
- 求最大下界：x∧y
子群格
对偶命题：令 f是将 f 中的≼替换成≽,≽替换成≼,∨替换成∧,∧替换成∨所得到的命题. 称 f 为 f 的对偶命题
子格S：S是L的非空子集，S关于L中的运算∧和∨仍构成格
分配格L：对所有a,b,c∈ L ，满足a∧(b∨c) = (a∧b)∨(a∧c)，a∨(b∧c) = (a∨b)∧(a∨c)
钻石格L₃,五角格L₄
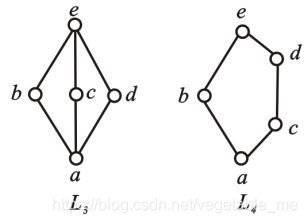
全下界0/全上界1：存在a使得所有x∈ L有a≼x /存在b使得所有x∈ L有x≼b
有界格L<L,∧,∨,0,1> ：格L存在全下界和全上界
补元b：有界格L中，对于a，存在b∈ L 使得a∧b = 0 和 a∨b = 1
- 有补格：所有元素都有补元
布尔代数/布尔格<B,∧,∨,’, 0, 1> ：有补分配格，’为求补运算
- (代数系统定义)满足交换律/分配律/同一律(a ∗1=a, a◦0 =a )/补元律(a ∗a’=0, a◦a’=1)的代数系统
- 原子a：L 是格, 0∈ L ,对所有b有0 ≺ b ≼ a 等价于 b = a

初等数论
-b|a(a%b==0)：a被b整除，b整除a

平凡因子：1和自身
真因子：非平凡因子
素数/合数
- 素因子分解
- pi(n): 小于等于n的素数个数
- 埃拉托斯特尼(Eratosthene)筛法：每次去掉一个素数及其倍数
公因子/最大公因子gcd(a,b)
- 辗转相除法/欧几里得算法：算最大公因子
公倍数/最小公倍数lcm(a,b)
同余a≡b(mod m) ：m是正整数, a和b是整数，满足m|a-b
- 等价类[a]/[a]_m：模m同余下的等价类
  - Z_m：Z在模m同余关系下的商集
同余方程ax≡c(mod m), 其中m>0
模m逆a^-1(mod m)/a^-1：如果ab≡1(mod m), 则称b是a的模m逆
欧拉函数Φ[n]：{0,1,…, n-1}中与n互素的数的个数
- n为素数Φ[n]=n-1，否则Φ[n]<n-1
线性同余产生伪随机数x_n=(ax_n-1+c) mod m, n=1,2,…
- 乘同余法: c=0(x0≠0)的线性同余法, 即x_n=ax_n-1 mod m, n=1,2,….
维吉尼亚密码：分组
RSA公钥密码：加密密钥w和n是公开的, 而p,q,Φ(n)和d是保密的
- 取素数p/q, n=pq, Φ(n)=(p-1)(q-1)
- 取正整数w（和Φ(n)互素）,加密c=E(m)=m^w mod n
- (解密)d=w^-1(mod Φ(n)) ,m=D( c )=c^d mod n
- （模幂乘运算）b=b₀+b₁× 2+…+b_r-1× 2^r-1，则a^b mod n≡a^b~0~ ×(a²)^b~1~ × …(a^{2的r-1次方})^b_r-1

定理

（唯一存在）零元和单位元只要存在，就是唯一的
（唯一存在）逆元存在则唯一
（零元和单位元）|S|>1，则e≠θ
（积代数性质）
- 因子代数运算可交换/结合/幂等则积代数运算可交换/结合/幂等
- 因子代数单位元e₁/e₂,零元θ₁/θ₂，则积代数单位元<e₁,e₂> ，零元<θ₁,θ₂>
- 因子代数x/y可逆，则积代数<x,y>也可逆，逆元是<x^-1,y^-1>
（群中的幂运算性质）
- （两次求逆等于本身）∀a∈ G, (a^-1)^-1=a
- （不同元素的逆相乘）∀a,b∈ G,(ab)^-1=b^-1a^-1
- ∀a∈ G, aⁿa^m = a^n+m, n, m∈ Z
- ∀a∈ G,(aⁿ)^m = a^nm, n, m∈ Z
- 若G为交换群,则 (ab)ⁿ = aⁿbⁿ ;不是则有(ab)ⁿ=(ab) (ab)…(ab)
（元素的阶）|a|=r,k是整数
- （元素阶存在）a^k=e 当且仅当 r|k(k%r==0)
- （元素和逆元的阶的关系） |a^-1|=|a|
（消去律）G适合消去律，任意元素a/b/c ab=ac或ba=ca 则 b=c
（唯一解）设G为群,∀a,b∈ G,方程ax=b和ya=b在G中有解且仅有惟一解.
（子群判定定理）H是G的非空子集，则H是G的子群当且仅当
- ∀a,b∈H 有ab∈H
- ∀a∈H 有a^-1∈H
（子群判定定理）设G为群， H是G的非空有穷子集，则H是G的子群当且仅当 ∀a,b∈ H有ab∈ H
（子群判定定理）H是G的非空子集，H是G的子群当且仅当 ∀a,b∈H有ab^-1∈H
（陪集性质）
- （单位元右陪集） He=H
- （代表元素属于陪集）∀a∈ G 有a∈ Ha
子群H和群G ∀a,b 有 a∈ Hb ⇔ ab^-1∈ H ⇔ Ha=Hb
（陪集性质）陪集之并为G；陪集要么相等，要么不相交
（Lagrange定理）有限群G，子群H，|G| = |H|·指数[G:H] (H在G中的不同陪集（左or右）数)
- （推论：元素的阶）n阶群G，则∀a∈ G, |a|是n的因子，且有aⁿ=e
- （推论：生成子群）对阶为素数的群G，必存在a∈ G使得G = < a >
- （推论：判定交换群）如果群 G 只含 1 阶和 2 阶元，则 G是Abel群
（无限循环群）只有两个生成元，即a和a^-1
（n阶循环群）G含有欧拉函数(n)（＜n且与n互素的正整数的个数，1算）个生成元
（循环群相关）
- （循环群子群）仍是循环群
- （无限循环群子群）除{e}以外都是无限循环群
- （n阶循环群）对n的每个正因子d， G恰好含有一个d阶子群
（等价类计数）Polya定理：着色方案是M=Σ(m^c(置换_k))/|G|
（素数）Fermat小定理：设 p为素数，则 p|(n^p-n)
（域）设 p为素数，则Z_p是域
初等数论
（整除性质）
- （整除的线性叠加性）若a |b且a |c, 则所有x, y, 有a | xb+yc.
- （整除传递）若a |b且b |c, 则a |c
- （消去律与整除）设 m≠0, 则 a |b 当且仅当 ma | mb.
- 若a | b且b≠0, 则|a|≤|b|.
- 若a | b且b | a, 则a=±b
（素数整除性质）设p是素数且p | ab, 则必有p | a 或者 p | b
- （推广）设p是素数且p | a₁a₂…a_k, 则必存在1≤i≤k, 使得p| a_i.
（素数个数）无穷多个素数
（梅森数）2^p-1, 其中p为素数 (n是合数，则2ⁿ-1一定是合数)
（素数定理）lim n→∞ pi(n)/(n/In n)=1
（合数的因子）如果a是合数, 则a必有小于等于根号a的真因子（素因子）
（辗转相除法）设a=qb+r, 其中a, b, q, r 都是整数, 则gcd(a,b) = gcd(b,r)
（公因子）设a 和 b 不全为0, 则存在整数 x 和 y 使得gcd(a,b) = xa+yb
（互素条件）整数a和b互素当且仅当存在整数x和y使得xa+yb=1
（同余性质）
- 自反/传递/对称
- （同余数的运算）若a≡b(mod m), c≡d(mod m), 则a±c≡b±d(mod m), ac≡bd(mod m),ak≡bk(mod m), 其中k是非负整数
- （模数）设d≥1, d | m, 则a≡b(mod m) ，则a≡b(mod d)
- 设d≥1, 则a≡b(mod m) 当且仅当 da≡db(mod dm)
- 设c,m互素, 则a≡b(mod m) 当且仅当 ca≡cb(mod m)
（同余方程有解）方程ax≡c(mod m)有解当且仅当 gcd(a,m)|c
（模m逆存在条件）a的模m逆存在当且仅当 a与m互素
（模m逆唯一）设a与m互素, 则在模m下a的模m逆是惟一的
（欧拉定理）设a与n互素, 则a^Φ(n)≡1(mod n)
（费马小定理）设p是素数, a与p互素, 则a^p-1≡1(mod p)
- 设p是素数, 则对任意的整数a,a^p≡a(mod p)
  格
（格和对偶格）f对所有格真，则其对偶命题对所有格也真
（基本不等式）
- 自反/传递/反对称
- （下界） a∧b ≼a, a∧b ≼b
- （上界） a∨b ≽ a, a∨b ≽b
- （下确界） a ≼b, a ≼c, 则 a ≼ b∧c
- （上确界） a ≽ b, a ≽ c, 则 a ≽ b∨c
（格）运算∨和∧适合交换律、结合律、幂等律和吸收律
（格的性质）设L是格, 则a,b∈ L有a ≼ b 等价于 a∧b = a 等价于 a∨b = b
（格的保序性）设L是格, 所有a,b,c,d∈ L，若a ≼ b 且 c ≼ d, 则a∧c ≼ b∧d, a∨c ≼ b∨d
（格的分配不等式）设L是格, 所有a,b,c∈ L有a∨(b∧c) ≼ (a∨b)∧(a∨c)
（判别分配格）L是分配格当且仅当 L不含有与钻石格或五角格同构的子格
（有界格性质）所有a∈ L有a∧0 = 0, a∨0 = a, a∧1 = a, a∨1 = 1
（有界分配格补元）若L中元素 a存在补元, 则存在惟一的补元
- （一般格）对于一般元素, 可能存在补元, 也可能不存在补元. 如果存在补元, 可能是惟一的, 也可能是多个补元
（布尔代数性质）
- （求补）(a‘)’ = a
- （德摩根律）(a∧b)’ = a’∨b’, (a∨b) ’= a’∧b’
（有限布尔代数）
- 设B是有限布尔代数, A是B的全体原子构成的集合, 则B同构于A的幂集代数P(A)
  - （基数）任何有限布尔代数的基数为2ⁿ, n∈ N
  - （同构性）等势的有限布尔代数同构