Simulink—Adams联合仿真：匀速圆周运动的控制

Simulink与Adams联合仿真实现匀速圆周运动控制

原创已于 2024-10-13 01:43:15 修改 · 2.2k 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #matlab

于 2024-07-28 19:24:39 首次发布

一、前言

用Adams和Simulink实现物体的匀速圆周运动

二、理论分析

我们知道，匀速圆周运动的动力学公式为式子（1）

F——圆周运动的向心力

M——运动物体的质量

V——匀速圆周运动的切向线速度

R——圆周轨迹半径

假设小球在XY平面上做匀速圆周运动，其运动轨迹半径为R，如图所示

分析上图，则存在式子（2）

这里有式子（3）和（4）

则式子（2）可改写为式子（5）

同理，向心力F和切向速度V分别为式子（6）和（7）：

这里θ是随着小球的运动时刻变化的，既随时间变化的（8）：

小球做匀速圆周运动时，我们知道其角速度和线速度存在关系（9）：

将（8）和（9）式替换掉前面所有式子中的θ，则我们找出了运动和力关于时间之间关系。同时可

以将圆周运动转化为在X轴和Y轴上的运动进行求解，即简谐运动的求解。

三、解法一 (开环控制)

1、匀速圆周条件

分析小球匀速圆周运动的过程，我们知道要满足以下条件：

（1）切向线速度V，大小保持不变，方向时刻改变

（2）存在一个力F为小球的运动提供向心力

2、初始位置状态

如果一个小球从静止状态开始，要达到圆周运动；则需要在一定时间内加速到指定线速度V，

之后在向心力的作用下开始做圆周运动。在XY平面中，要使小球绕原点O做匀速圆周运动，存在两

种三种情况：

a.小球在运动轨迹范围内：

这种情况下，可以控制小球做螺旋线运动，但需要小球在达到圆周轨迹上的时候速度也刚好

满足要求，然后再向心力的作用下做圆周运动。

b.小球刚好在运动轨迹上：

此种情况下需要小球在极短的时间内加速到指定的切向线速度，之后再提供向心力。

c.小球在运动轨迹外：

此中情况与a类似。可以按照a的方法进行处理。

3、设定初始位置

设想一种特殊状态如图所示，小球4处在XY坐标系第一象限，我们可以先让小球4直线加速到

目标速度V和目标位置小球3处，然后撤销直线加速度a，同时添加向心力F。理论上小球4达到小

球3位置后，开始进行匀速圆周运动，按此理论创建Adams模型。

其中小球1表示运动中心，连杆2表示运动半径，小球3表示运动轨迹上的点，小球1、3和连

杆2都是固定不动的（Adams中作为参考物体）。小球4是我们需要进行控制做圆周运动的。

图中：

小球1位置(X,Y,Z)=(0,0,0)；

连杆2长度(X1,Y1,Z1)=(0,0,0)，(X2,Y2,Z2)=(0.45,0,0)；

小球3位置(X,Y,Z)=(0,0.45,0)；

小球4位置(X,Y,Z)=(0.4,0.45,0)。

4、Adams模型创建

（1）新建模型

新建模型——模型名称：Circle_Ball——选择无重力状态——单位选择(米、千克、牛、秒、

度)：MKS（M、kg、N、s、deg）——选择一个工作路径（不能有中文名称），点击确定

即可。

a. 创建小球1：

点击物体——球——半径处可以勾选后自己输入指定半径（注意这里单位是厘米cm），

也可以不勾选拖动达到自己觉得合适的尺寸。这里我选择小球半径5cm（5cm只是为了画面

协调，大小不影响结果的输出）。位置可以直接选择坐标原点位置即可创建成功。

b. 创建连杆2：

选择连杆，长、宽、深可以不用指定。然后点击左边原点处，会自动捕捉参考点，然后任意

位置右键弹出坐标对话框，可以将上述中连杆的第二个坐标复制输入进去，点击应用即可创

建连杆。

PS.如果没有自动捕捉到或者无法自动捕捉，是因为右下角的坐标图标没有打开，点击打开即可。

c.小球3和小球4也是类似的创建，这里以小球4作为演示：

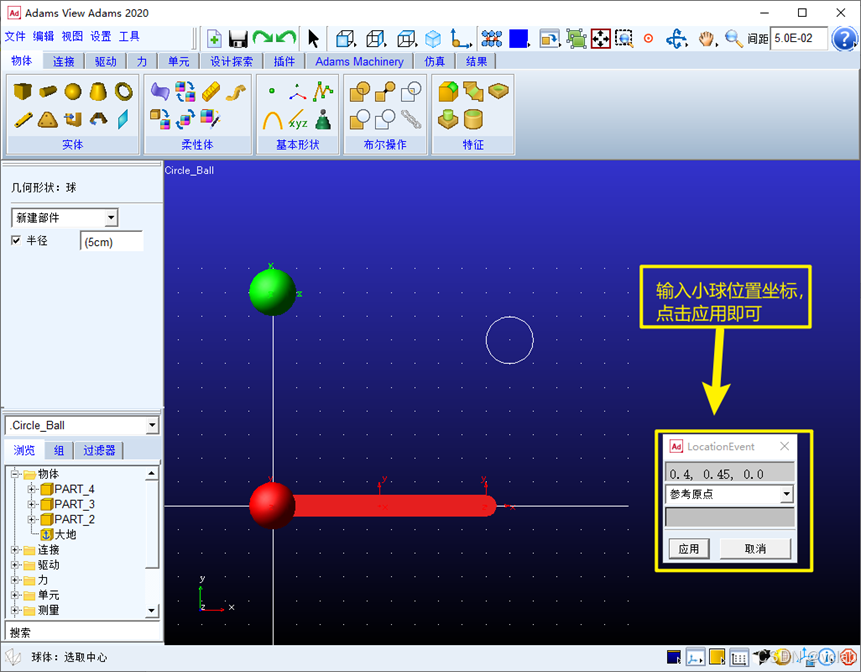
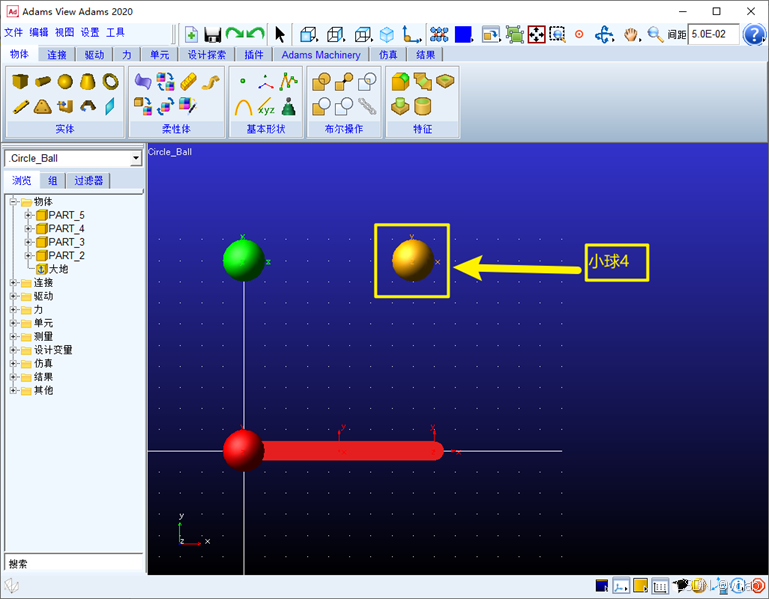
双击小球4——part_5，则显示小球的相关信息如下

将定义质量方式更改为用户输入，输入质量4.5，即表示小球质量4.5kg。其余参数保持默认即可。

其他小球和连杆是保持固定不动的，因此无需更改质量和相关属性。

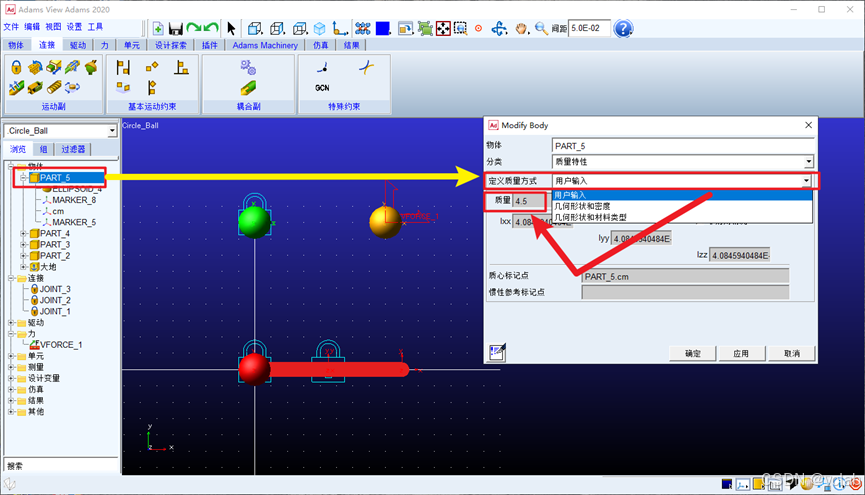
PS. 这里输入重量的原因是，Adams自己根据材料体积和密度求解出来的重量小数位数很多，我

们也可以自己定义重量、材料或者密度。这里为了计算方便，直接定义重量。

如何修改：重量按照上述方法进行修改；

修改密度则选择——几何形状和密度

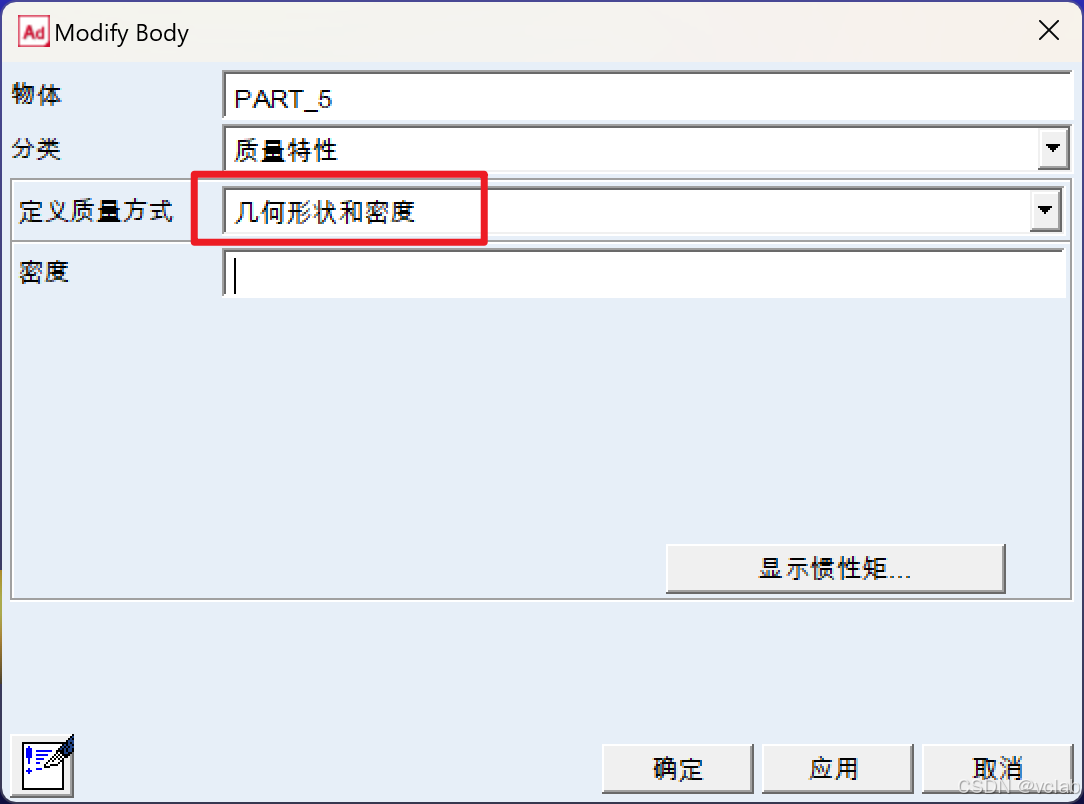
修改材料——几何形状和材料

（2）添加约束

创建完成所有所需模型，在该系统中，只有小球4是可以运动的，其他的都是固定作为参考的。

因此需要对小球1、3和连杆2进行固定。

（1）添加固定副

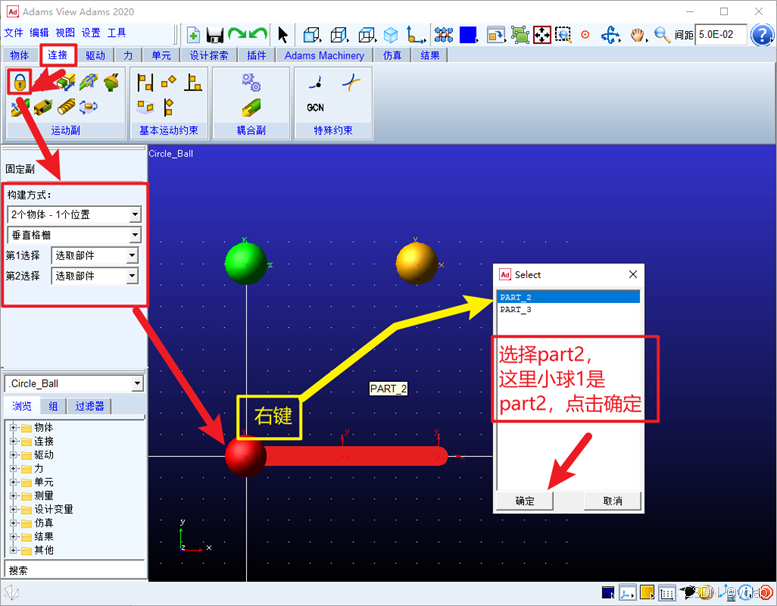
按图中操作后后选择地面（ground），再在原点位置右键找到小球质心（part2.cm）,选择质

心，点击确定，可以看到一个锁图标，即表示对小球1进行固定成功。

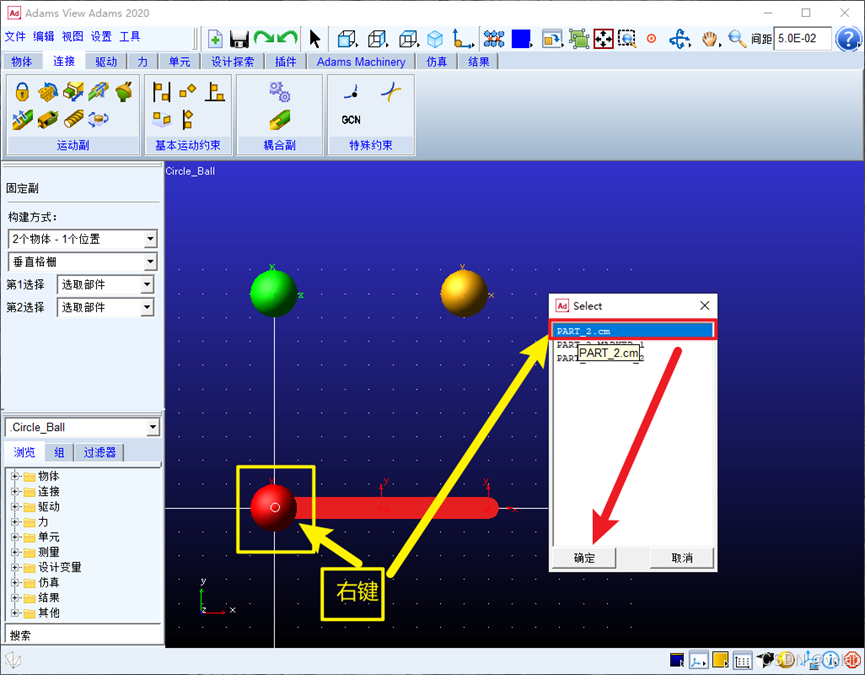
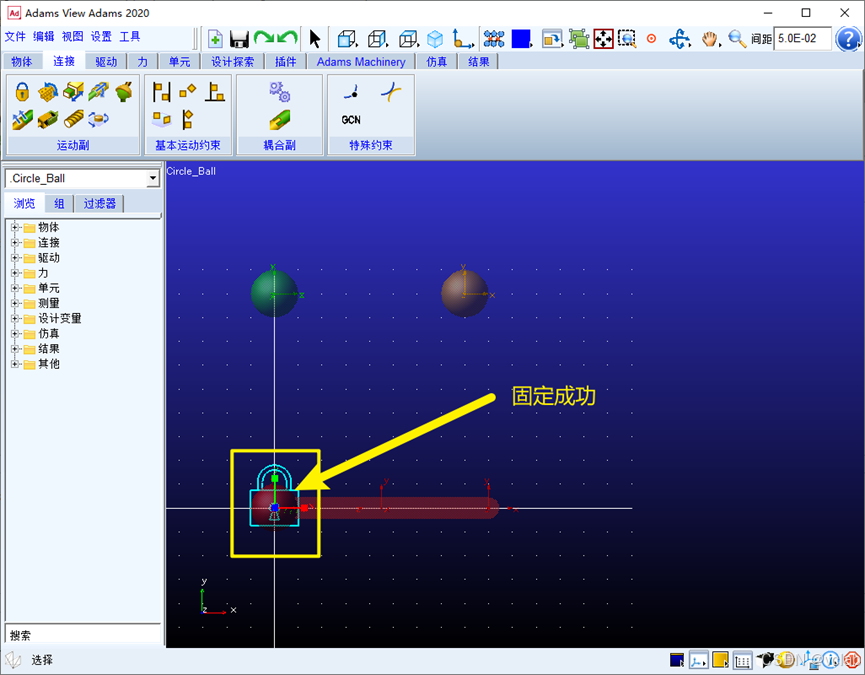
同理，连杆2和小球3也是一样的操作方式，这里不做演示了。需要说明的是连杆2无论是固定

在原点（0，0，0），质心（0.225，0，0）还是在连杆的另一端（0.45，0，0）都是可以的。按

上述顺序的质心分别是：

小球1质心：part_2.cm——（0，0，0）

连杆2质心：part_3.cm——（0.225，0，0）

小球3质心：part_4.cm——（0.45，0，0）

小球4质心：part_5.cm——（0.4,，0.45，0）

完成约束后再左边栏连接下面会有三个连接关系。

（2）添加力

完成固定部件的约束后，要使小球4动起来，则需要向它施加一定的力。前面我们分析过，要

是小球能在XY平面内做圆周运动，一个方向上的力是显然是不够的，向心力的大小不变，但方向

是时时变化的，因此需要X和Y方向上都有力。形成的合力始终由小球4质心指向圆心O。

在adams中给我们供了三向矢量力的添加方式：

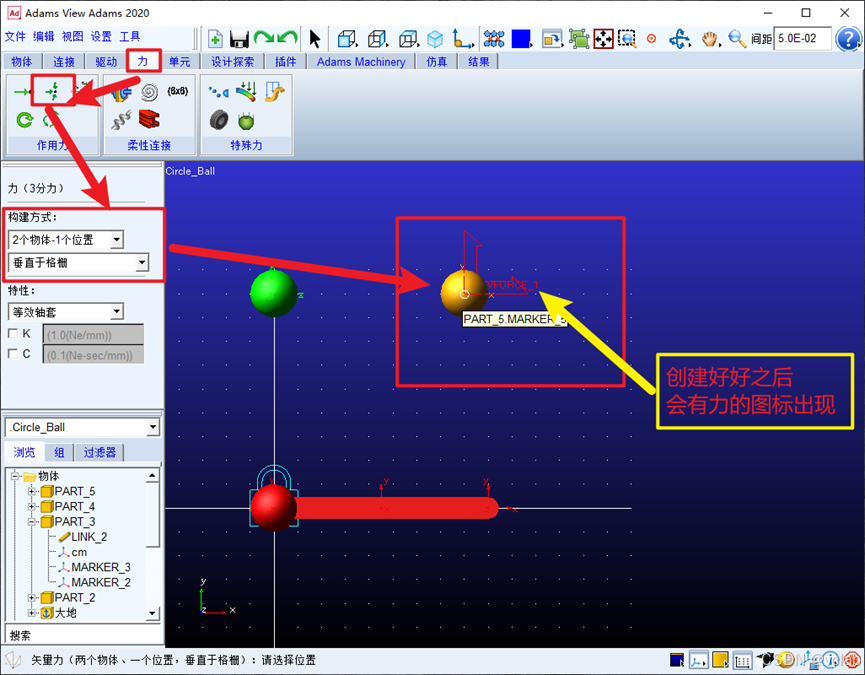
在左边栏力一栏中能看到我们刚创建的力矢量VFORCE_1，双击即可进行修改。打开之后，

因为小球只在XY平面内运动，因此，这里我们将Z方向的力设置为0。X和Y方向上大家可以试着不

同的力的效果。如果小球4可以运动，则说明模型是正确的。

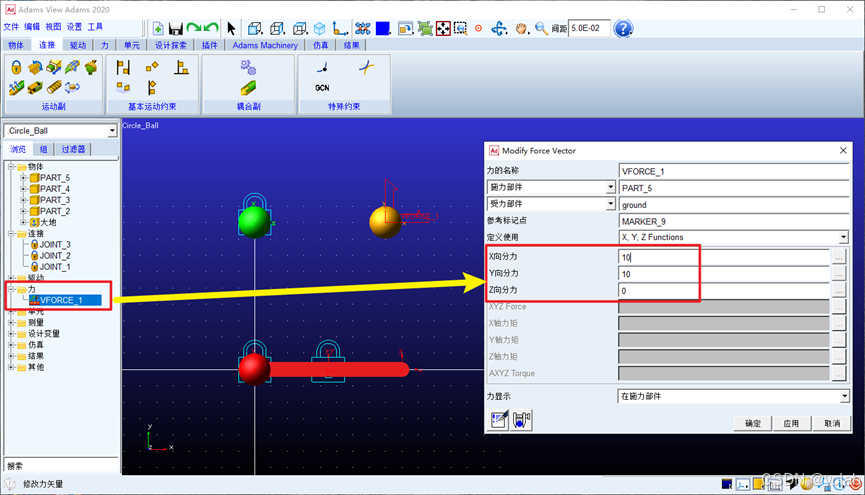
我这里设置X方向10，Y方向10，则运行之后如图所示

PS.针对上述模型，在Adams中单独实现圆周运动的问题，会在最后进行补充。

（3）添加连接单元

完成基本模型的创建和约束的建立之后，需要创建Adams和Simulink的接口。对于整个

Adams模型来说，我的输入是X方向和Y方向的力，输出是小球在X和Y方向上的位移变化情况。

a. 创建输入力

按图创建单元，名称可改为FX_X（不要命名为FX和FY，因为FX和FY是Adams的函数,是获

取关于X轴和Y轴合力的，图示为错误演示，请更改为FX_X)，F(time,…)保持为0，不需要填写。

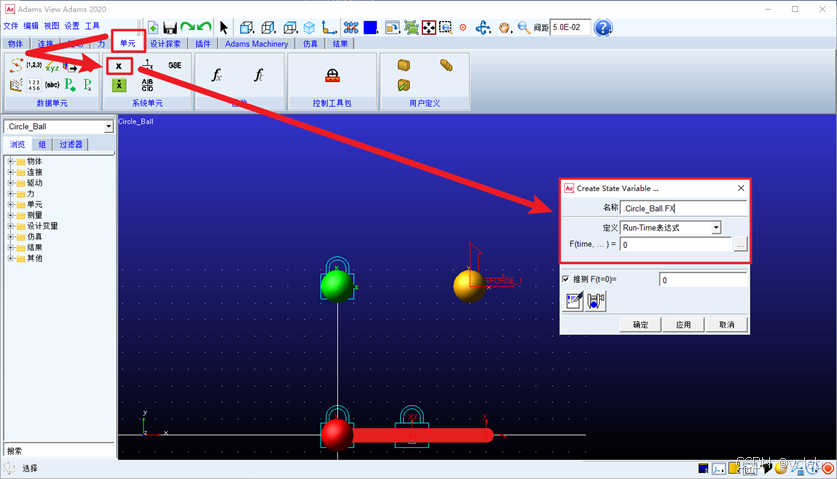
同理，创建FY_Y。

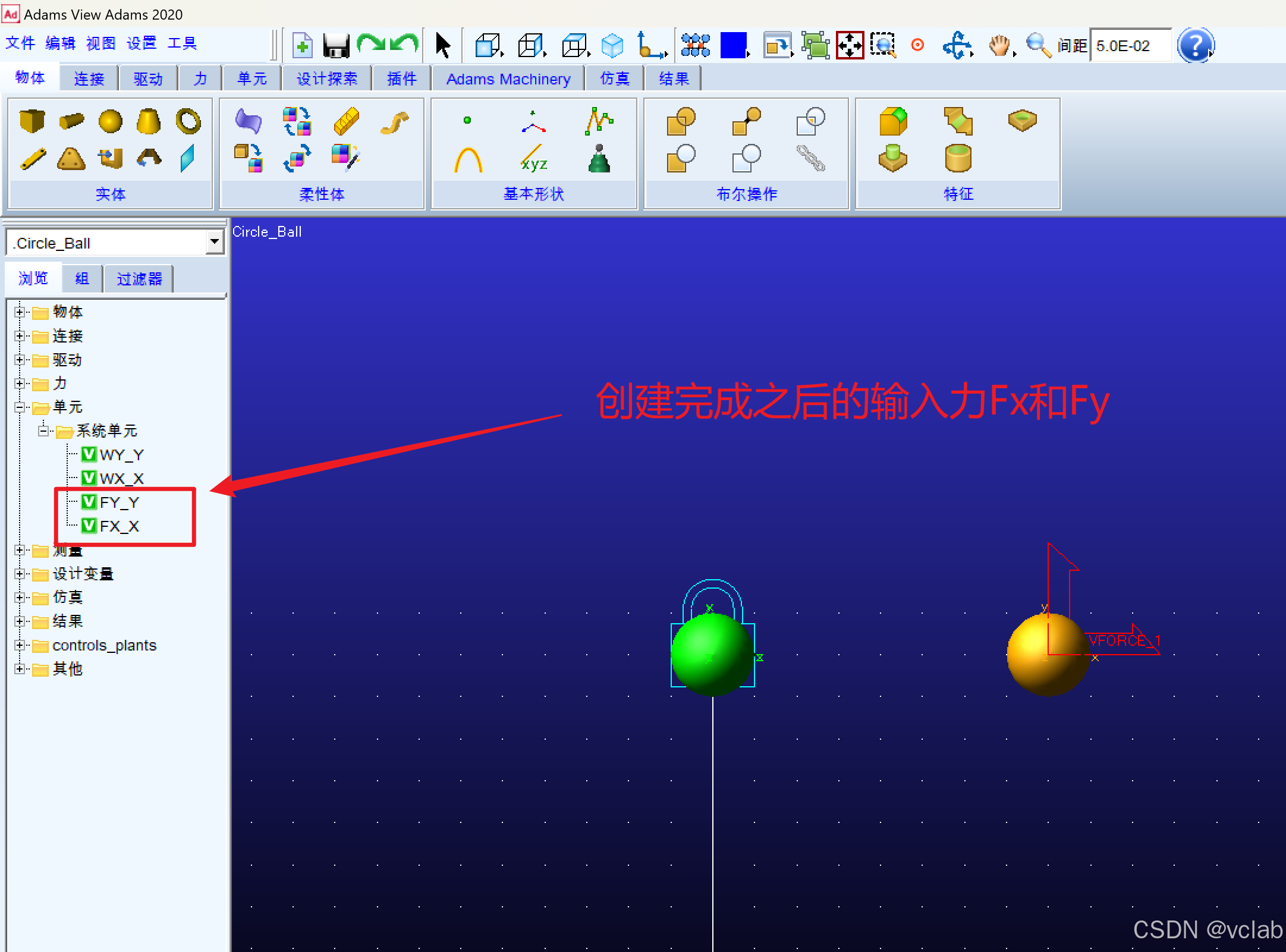
b. X位移的输出

完成输入力的创建之后，需要进行输出的创建单元——更改名称为WX_X（不要命名为WX和

WY，因为WX和WY是Adams的函数，是获取关于X轴和Y轴的角速度）表示X轴的位移，

F(time,…)右边三个点，点击一下，在辅助一栏下拉找到位移，找到“Distance along X”,双击

“Distance along X”，将定义运行时间函数编辑栏中的0删掉，同时删掉括号内的全部内容，输入小

球4的质心（Part_5.cm）——DX(Part_5.cm)。

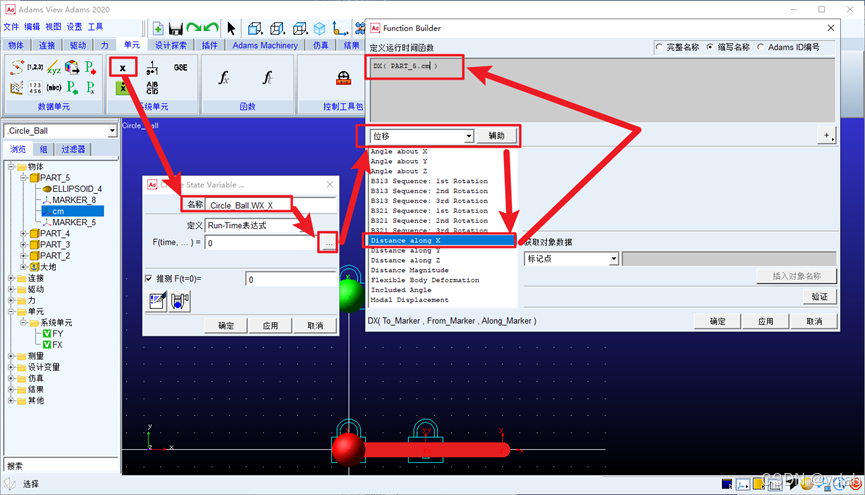点击验证——函数语法正确，则一直点击确定即可

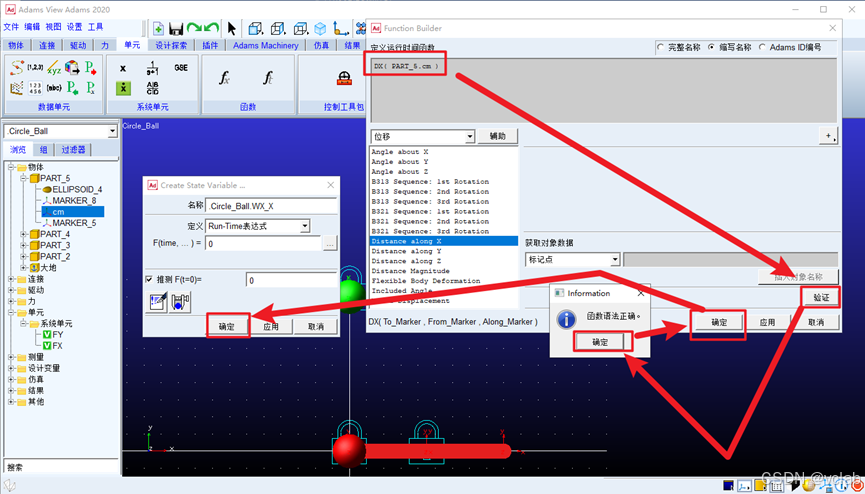PS. 关于小球4的质心获取方式：点开小球4的部件Part_5，找到cm，双击，将位置栏中的

Part_5.cm复制下来，填入前面位移函数的括号中去即可。

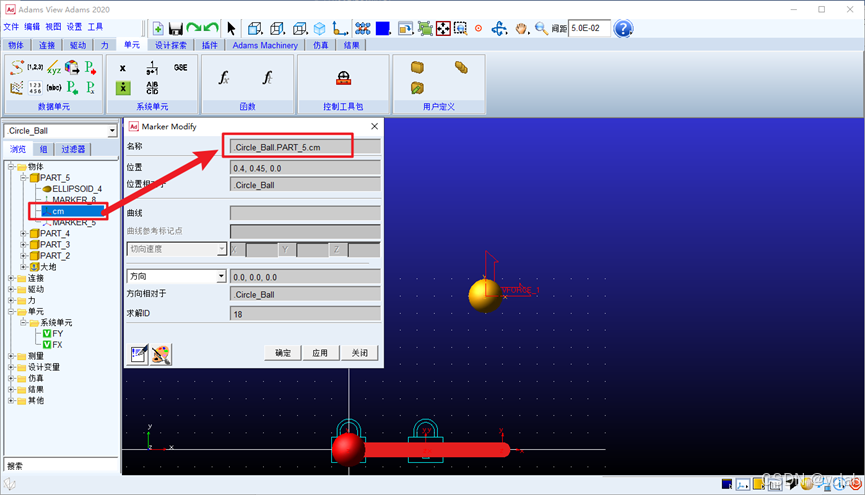
c. Y位移的输出

Y 方向的位移创建与X方向的类似，只是这里的位移函数需要更改为关于Y轴的

“Distance along Y”，括号中同样填入小球的质心“DY(Part_5.cm)”。

至此，完成所有Adams模型的创建，接下来需要将其导出为Simulink模型。

PS. 小球是在三维空间中的，在“添加约束”一节中，我们添加的是三向力，但因为我们的小球是

在XY平面上做运动，不考虑Z轴上的，因此将Z轴上的力设定为恒定值0，所以在添加单元的

时候无需添加Z轴上的FZ_Z。感兴趣的小伙伴也可以自己按照FX_X和FY_Y的添加方式去添

加FZ_Z，然后去连接测试一下，看看能否实现空间球面运动。

（4）Adams模型导出Simulnk

a. 确保插件开启

工具——插件管理器——第一项“Adams Controls”后面的都打勾。

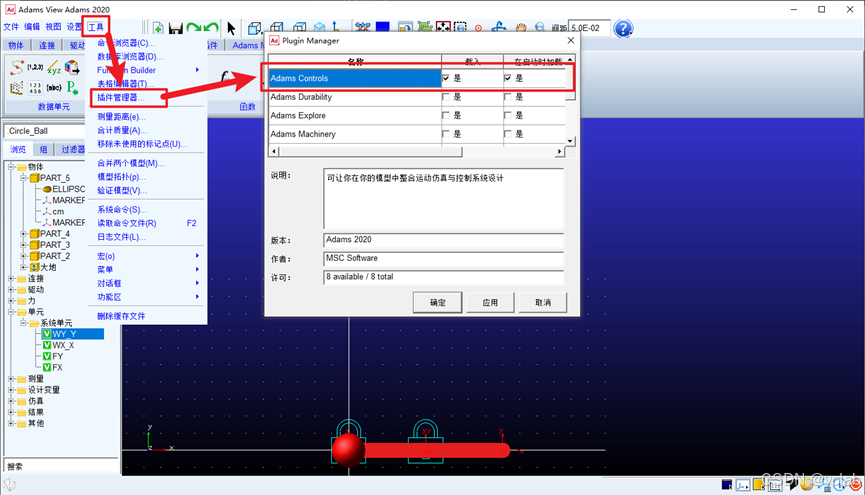
b. 机械系统导出

插件——机械系统导出——输入信号处右键——Adams变量——推测——找到FX和FY，

同理，输出信号处右键——Adams变量——推测——找到WX_X和WY_X，点击确定即可导出。

5、Simulink模型创建

（1）Adams模型打开

上面已完成模型的导出，现在打开matlab，切换路径到我们创建Adams模型工作路径的文件

夹下，直接运行Controls_Plant_1.m，之后我们会看到matlab工作区有很多关于Adams的参数，命

令行窗口也会显示关于输入FX_X、FY_Y和输出WX_X和WY_Y。

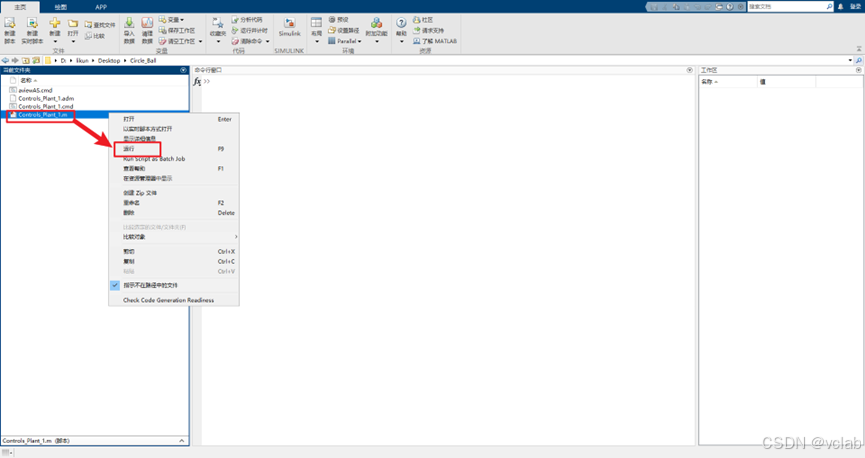
大家有兴趣也可以打开Controls_Plant_1.m文件，查看里面的代码，以及一些参数的设定。Controls_Plant_1.m模型全部代码详情（仅展示，不能运行，抹除了主机信息）

% Adams / MATLAB Interface - Release 2020.0.0
global ADAMS_sysdir; % used by setup_rtw_for_adams.m
global ADAMS_host; % used by start_adams_daemon.m
machine=computer;
datestr(now)
if strcmp(machine, 'GLNXA64')
   arch = 'linux64';
elseif strcmp(machine, 'PCWIN64')
   arch = 'win64';
else
   disp( '%%% Error : Platform unknown or unsupported by Adams Controls.' ) ;
   arch = 'unknown_or_unsupported';
   return
end
   [flag, topdir]=system('adams2020 -top');
if flag == 0
  temp_str=strcat(topdir, '/controls/', arch);
  addpath(temp_str)
  temp_str=strcat(topdir, '/controls/', 'matlab');
  addpath(temp_str)
  temp_str=strcat(topdir, '/controls/', 'utils');
  addpath(temp_str)
  ADAMS_sysdir = strcat(topdir, '');
else
  addpath( 'D:\ADAMS2020\controls/win64' ) ;
  addpath( 'D:\ADAMS2020\controls/matlab' ) ;
  addpath( 'D:\ADAMS2020\controls/utils' ) ;
  ADAMS_sysdir = 'D:\ADAMS2020\' ;
end
ADAMS_exec = '' ;
ADAMS_host = '************' ;
ADAMS_cwd ='**************'  ;
ADAMS_prefix = 'Controls_Plant_2' ;
ADAMS_static = 'no' ;
ADAMS_solver_type = 'C++' ;
ADAMS_version = '2020' ;
if exist([ADAMS_prefix,'.adm']) == 0
   disp( ' ' ) ;
   disp( '%%% Warning : missing Adams plant model file(.adm) for Co-simulation or Function Evaluation.' ) ;
   disp( '%%% If necessary, please re-export model files or copy the exported plant model files into the' ) ;
   disp( '%%% working directory.  You may disregard this warning if the Co-simulation/Function Evaluation' ) ;
   disp( '%%% is TCP/IP-based (running Adams on another machine), or if setting up MATLAB/Real-Time Workshop' ) ;
   disp( '%%% for generation of an External System Library.' ) ;
   disp( ' ' ) ;
end
ADAMS_init = '' ;
ADAMS_inputs  = 'FX_X!FY_Y' ;
ADAMS_outputs = 'WX_X!WY_Y' ;
ADAMS_pinput = 'Controls_Plant_2.ctrl_pinput' ;
ADAMS_poutput = 'Controls_Plant_2.ctrl_poutput' ;
ADAMS_uy_ids  = [
                   1
                   2
                   3
                   4
                ] ;
ADAMS_mode   = 'non-linear' ;
tmp_in  = decode( ADAMS_inputs  ) ;
tmp_out = decode( ADAMS_outputs ) ;
disp( ' ' ) ;
disp( '%%% INFO : ADAMS plant actuators names :' ) ;
disp( [int2str([1:size(tmp_in,1)]'),blanks(size(tmp_in,1))',tmp_in] ) ;
disp( '%%% INFO : ADAMS plant sensors   names :' ) ;
disp( [int2str([1:size(tmp_out,1)]'),blanks(size(tmp_out,1))',tmp_out] ) ;
disp( ' ' ) ;
clear tmp_in tmp_out ;
% Adams / MATLAB Interface - Release 2020.0.0

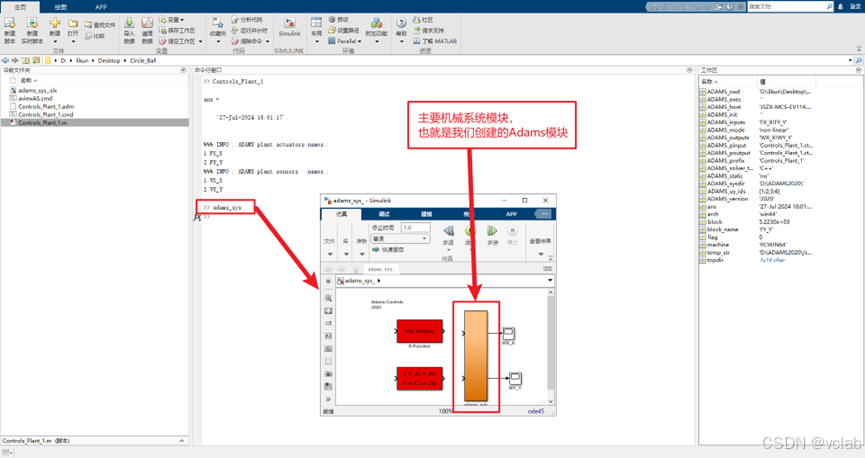
（2）matlab命令行窗口输入：

adams_sys

回车后弹出Simulink模型。将主要机械系统模块复制到我们新建的Simulink模型中去，不要在弹出的模型上进行修改。

（2）Simulink控制仿真

a. 特殊情况

在本章第3节中我们做了设想，先让小球4加速到速度V，并且位移达到X，也就是到达小球3

位置时，取消提供X方向加速度的力Fx1，然后在小球3位置开始，由Fx和Fy共同作用提供向心力

F。

我们假设2秒钟之后小球4达到小球3位置，小球4从初始位置开始运动到小球3的位置时一个初

速度为0的加速运动，这个过程可以是匀加速，也可以是非匀加速。为求解方便我们可以设定为匀

加速运动。此时我们可以根据匀加速直线运动的运动学公式：

$x=\frac{1}{2}at^2$

$v=at$

X方向位移 x已知，为0.3m，时间t已知，为2秒。带入即可求得加速度a，从而求的速度t=2s

时刻的速度v。将带入第二章公式（1）中，即可求得向心力F的大小。同时将v带入第二章公式（9），得到匀速圆周运动的角速度，从而得出X方向和Y方向的力Fx和Fy与向心力F、速度

V、时间t之间的关系：

$Fx=F*cos(\frac{V}{R}*t)$

$Fy=F*sin(\frac{V}{R}*t)$

b. 一般情况

针对上述特殊情况，这里不再过多赘述，下面我们考虑一般情况下，即非匀加速度的直线运动。

假设加速度a与时间t存在某种关系。我们这里设置为：

$a_{x}=At^2+Bt+C$

系数A、B、C可以通过外部环境进行调整（大家也可以设定为其他函数关系，前提是要保证时间

t > 0时，ax是恒大于等于0的，否则不同系数下可能导致先加速后减速或先反向后正向，无法达到

预定位置）。这里设A=0.2，B=0.6，C=0，其他系数大家可以自己去测试。

将上述参数全部整理如下：

小球4质量M： M=4.5kg

初始目标位移X： X=0.4m

轨迹半径R： R=0.45m

加速度ax的时间系数： A=0.2， B=0.6， C=0；

c. 算法逻辑

沿着X轴负方向加速运动，当运动达到小球3位置时，加速度ax为0，此时开始提供向心

力，在小球3位置时，Fx应该沿着X轴正方向，值为0；Fy沿着Y轴负方向，值为F，在

这个过程中需要求出小球4达到小球3位置时的时间t和速度V，然后分别记为Tmax和Vmax。然后

将Tmax和Vmax带入：

$Fx=F*cos(\frac{V}{R}*t)$

$Fy=F*sin(\frac{V}{R}*t)$

同时在小球3位置时，Fx应该沿着X轴正方向，值为0；Fy沿着Y轴负方向，值为F，带入Tmax和

Vmax，则上式中需要加上一个相位
，即：

$Fx=F*cos(\frac{Vmax}{R}*Tmax+ \varnothing )$

$Fy=F*sin(\frac{Vmax}{R}*Tmax+\varnothing )$

满足Fx和Fy的初始值要求，则：

$cos(\frac{Vmax}{R}*Tmax+ \varnothing )=0$

$sin(\frac{Vmax}{R}*Tmax+\varnothing )=1$

即（这里的pi即圆周率π）：

$\frac{Vmax}{R}*Tmax+ \varnothing = \tfrac{pi}{2}$

得到：

$\varnothing = \tfrac{pi}{2}-(\frac{Vmax}{R}*Tmax)$

则完整的Fx和Fy的计算应该为：

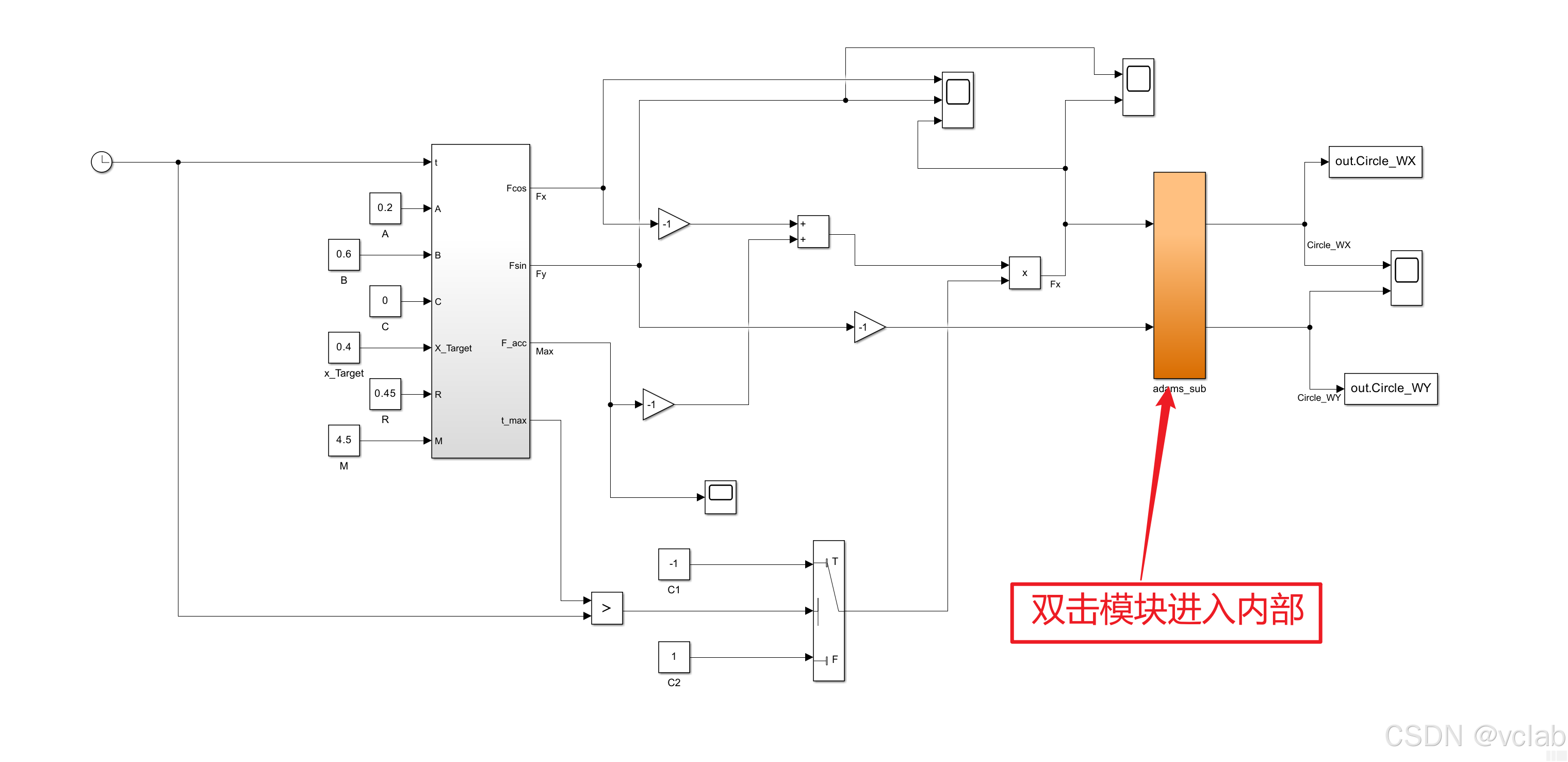
$Fx=F*cos(\frac{V}{R}*t+ \tfrac{pi}{2}-(\frac{Vmax}{R}*Tmax) )$

$Fy=F*sin(\frac{V}{R}*t+ \tfrac{pi}{2}-(\frac{Vmax}{R}*Tmax) )$

综上，在Simulink中实现算法如下：

模型解读（从左到右）：

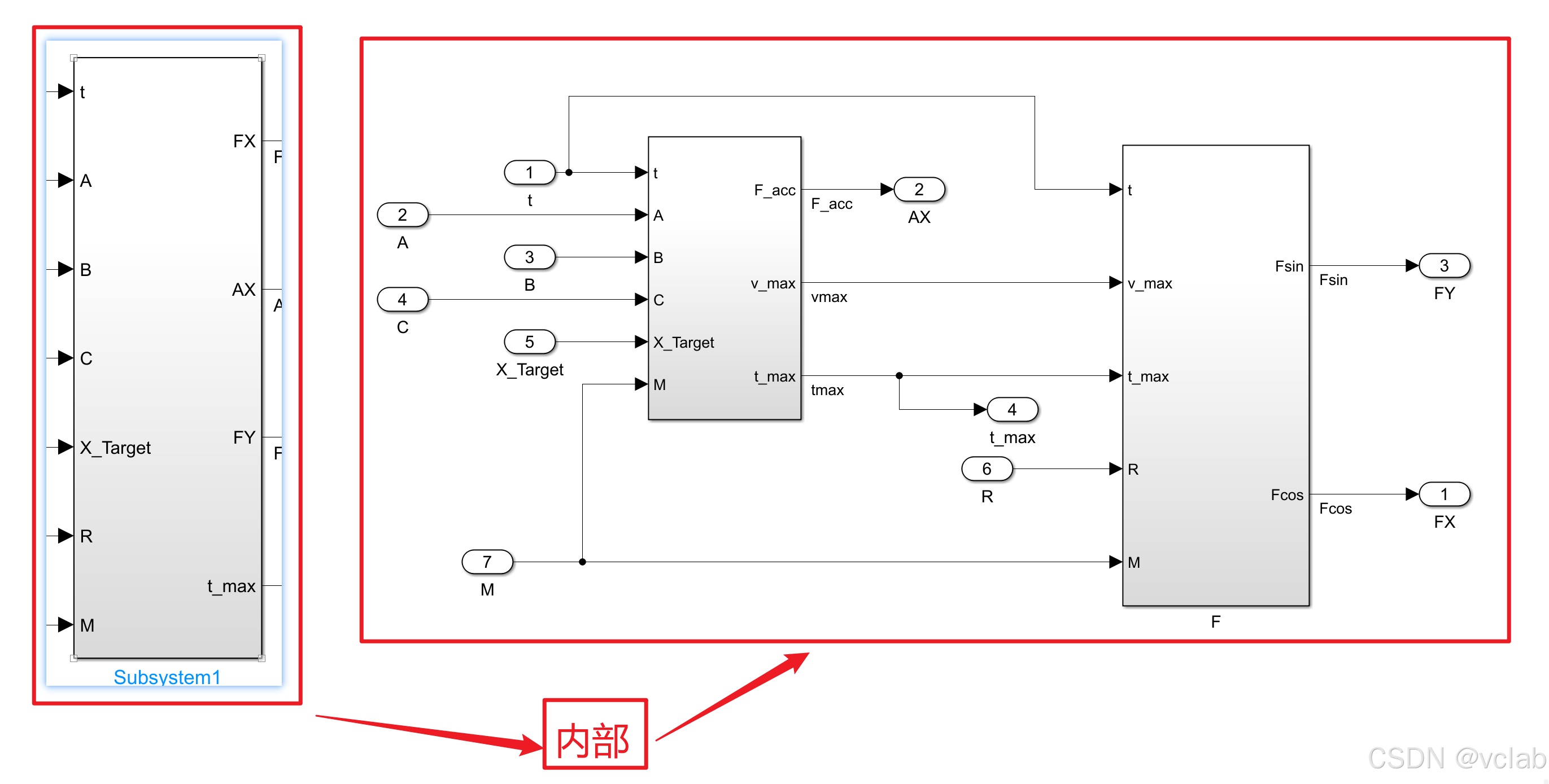
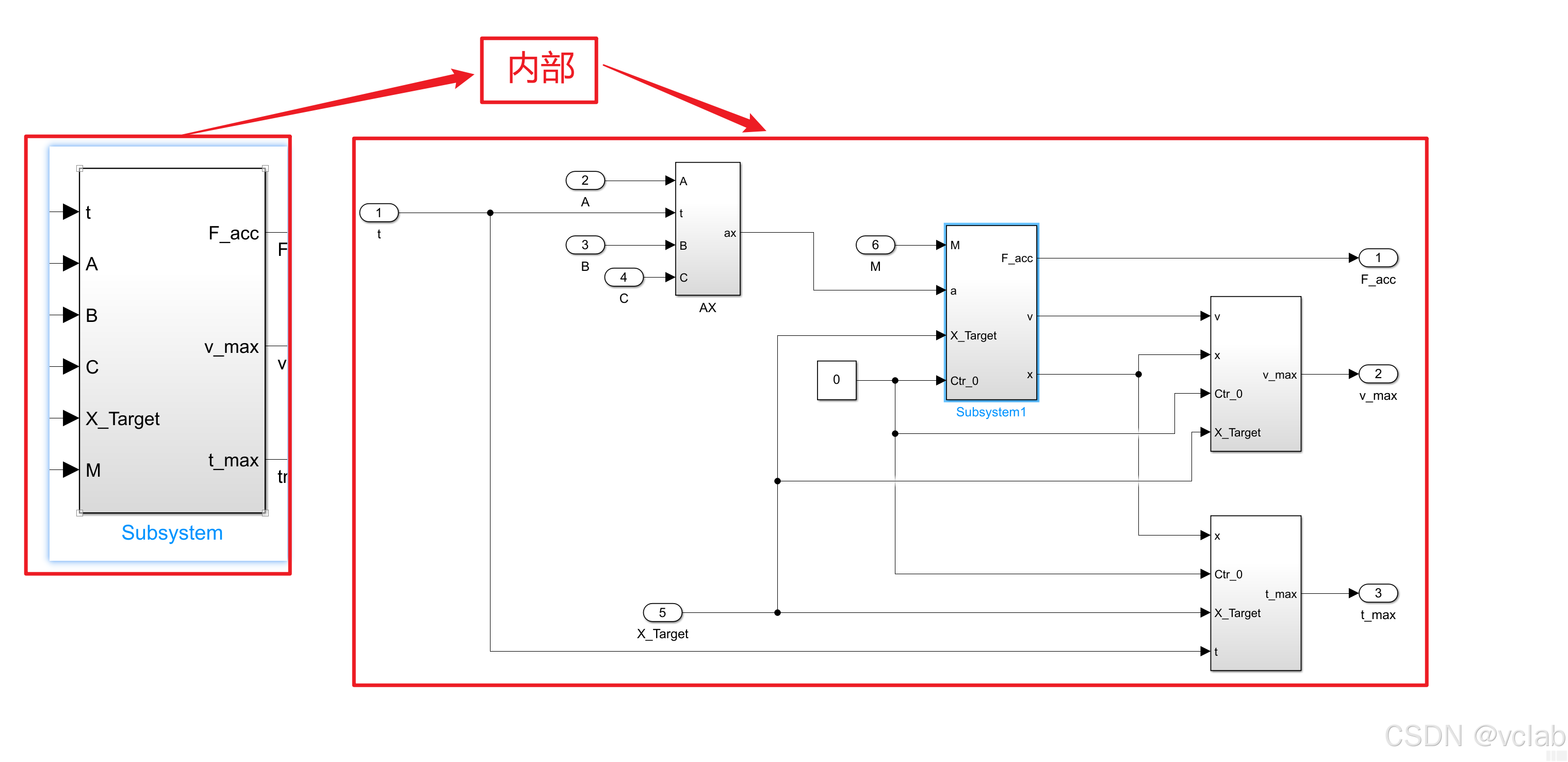
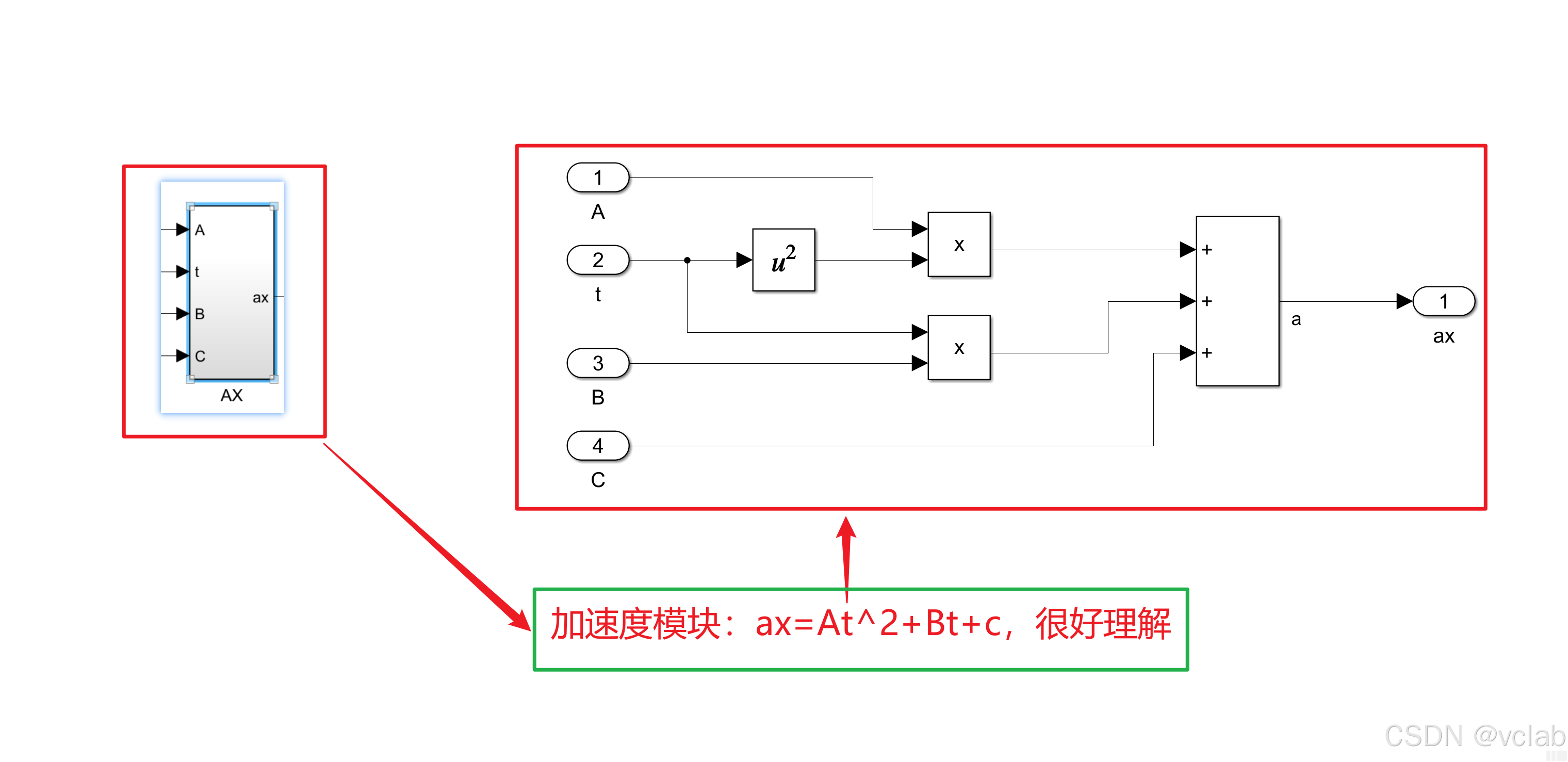接下来需要求出Tmax和Vmax（时间久了，暂时看不懂了，等理解了再来解释）：

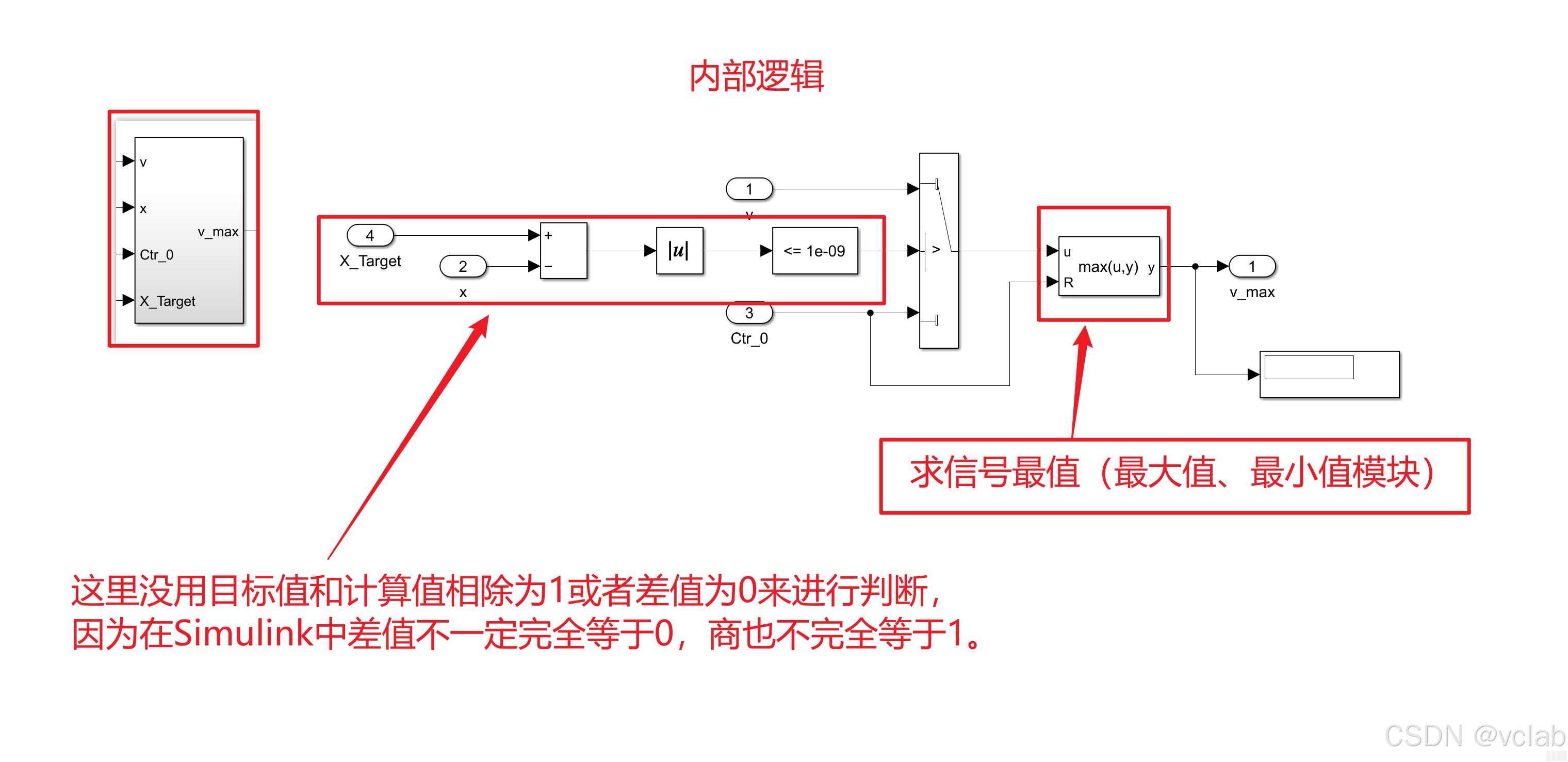
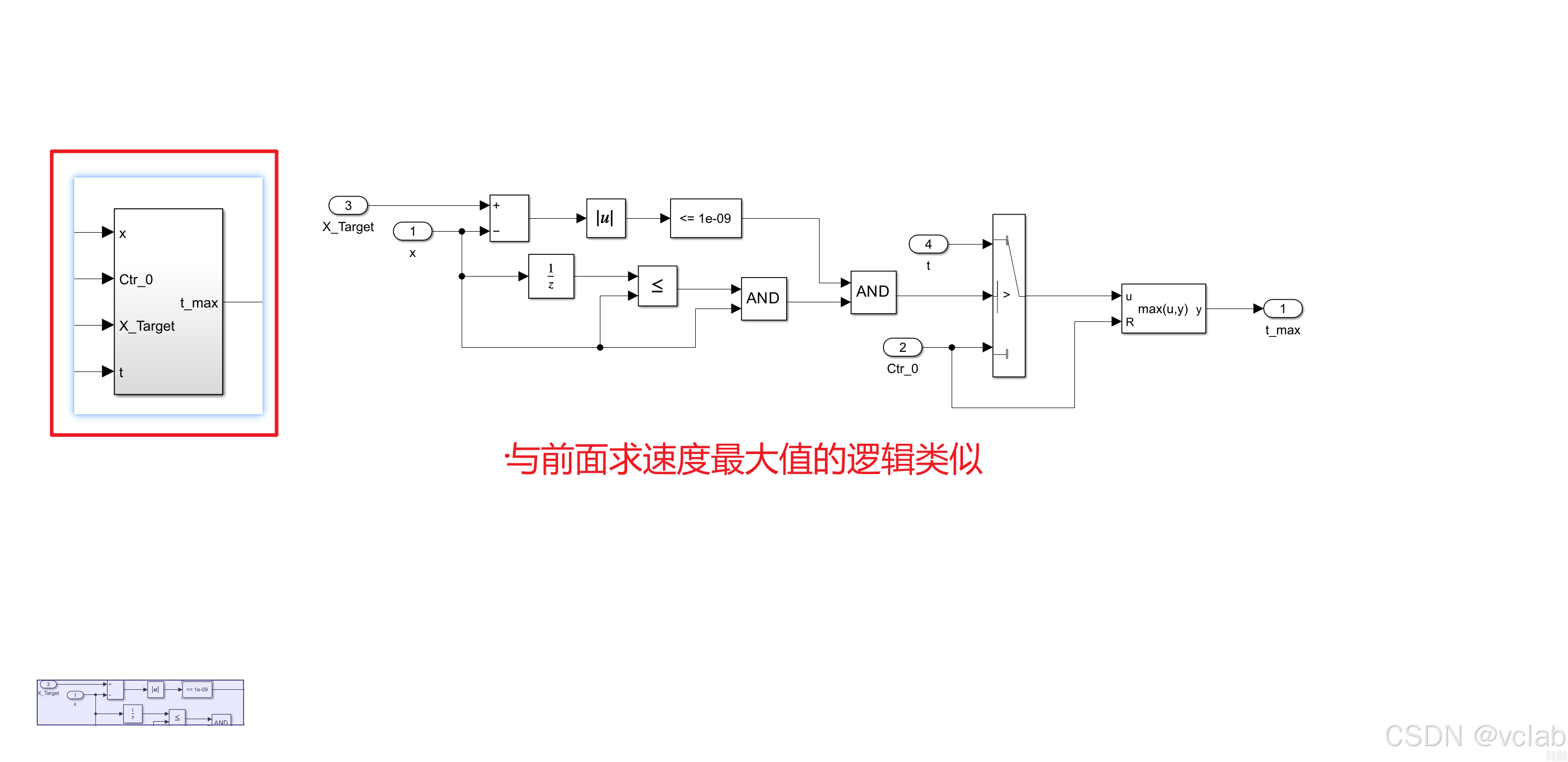
d. 实现仿真

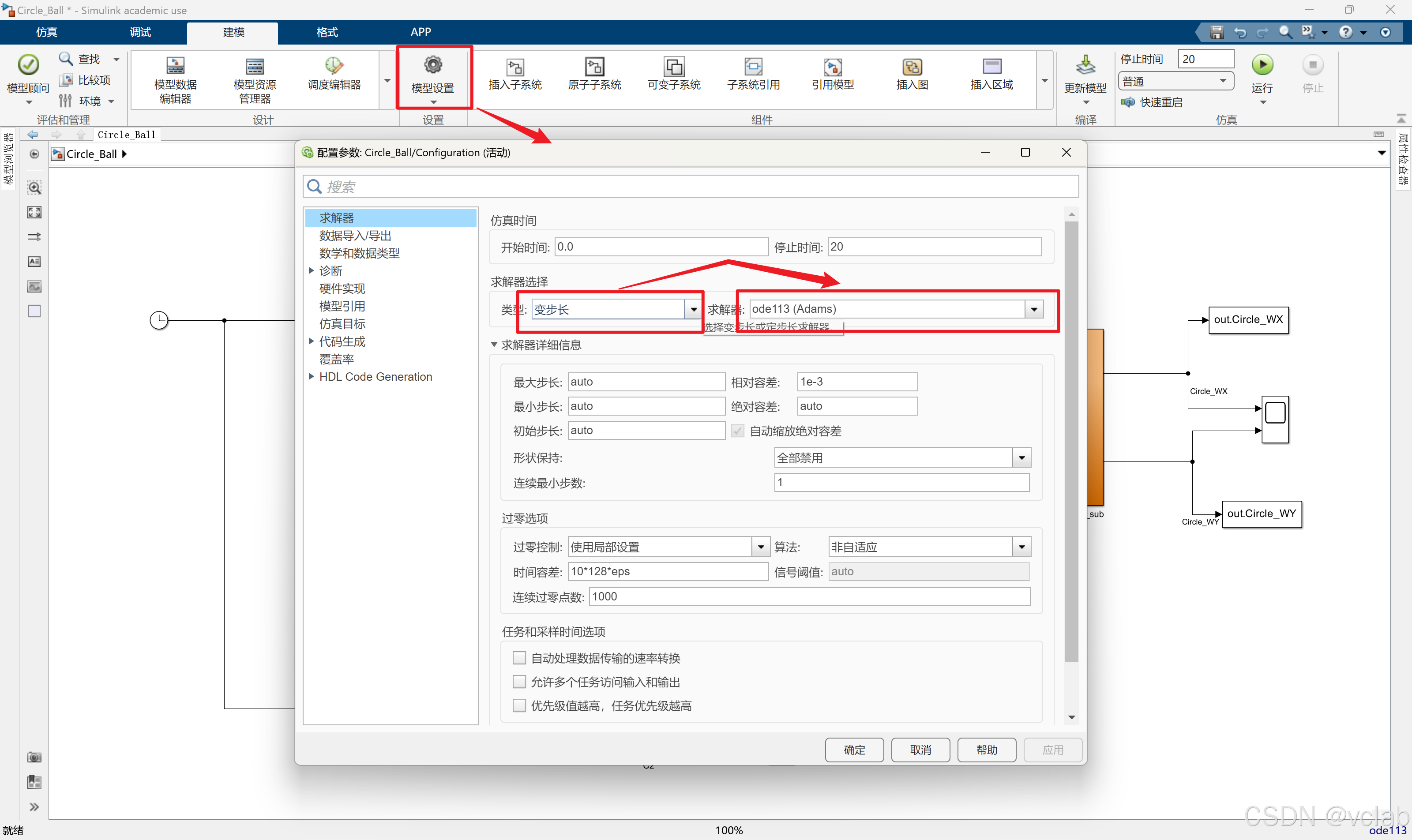
前面已完成Simulink的算法模型建立，在建模——模型设置（或快捷键Ctrl+E）在变部长类型

下选择ode113(Adams)求解器，仿真时间设置20秒。

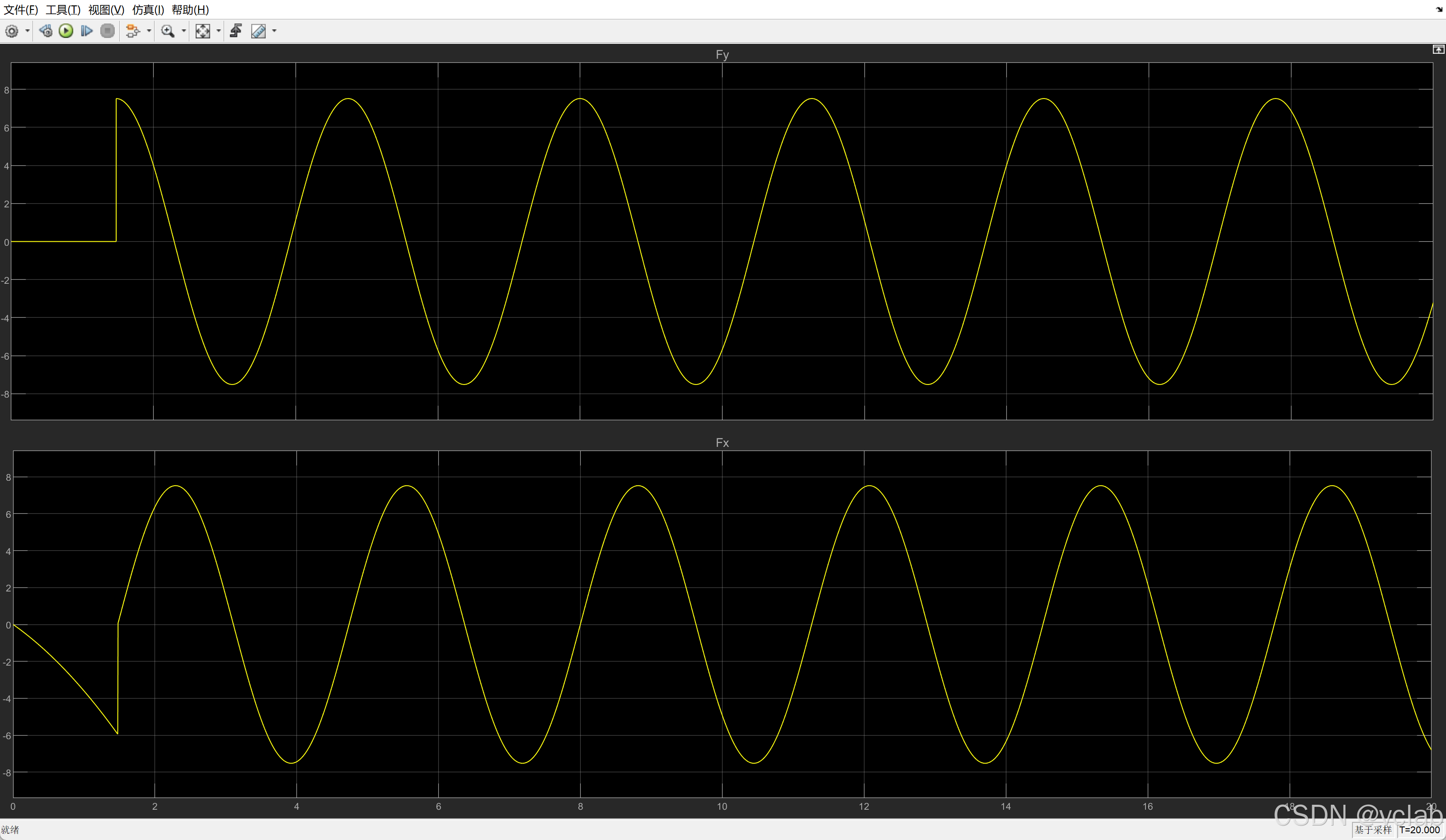
可以将示波器模块连接需要查看的模块，点击运行后查看示波器：

Fx和Fy的曲线（符合期望）：

Wx和Wy（也符合期望）：

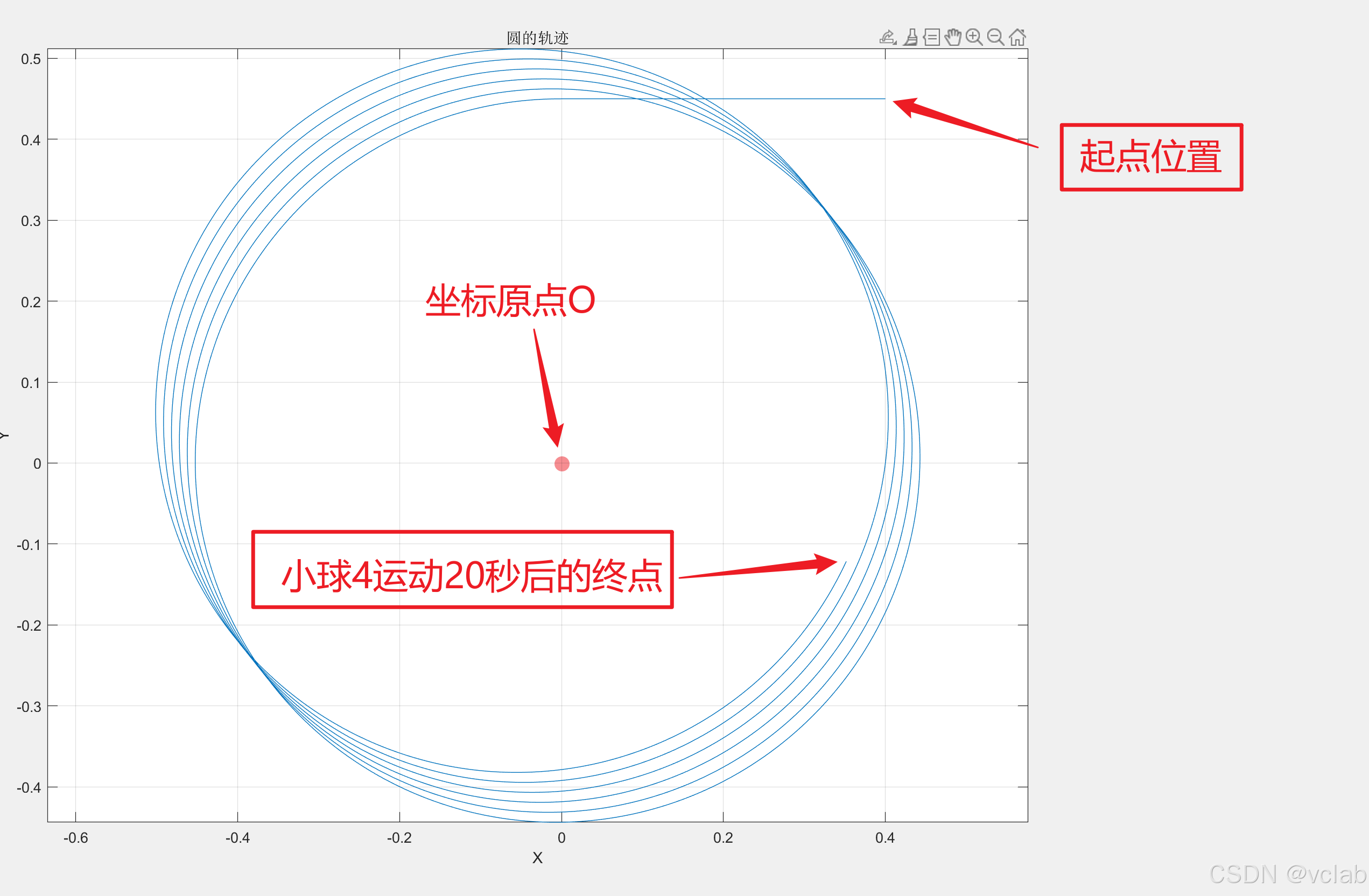
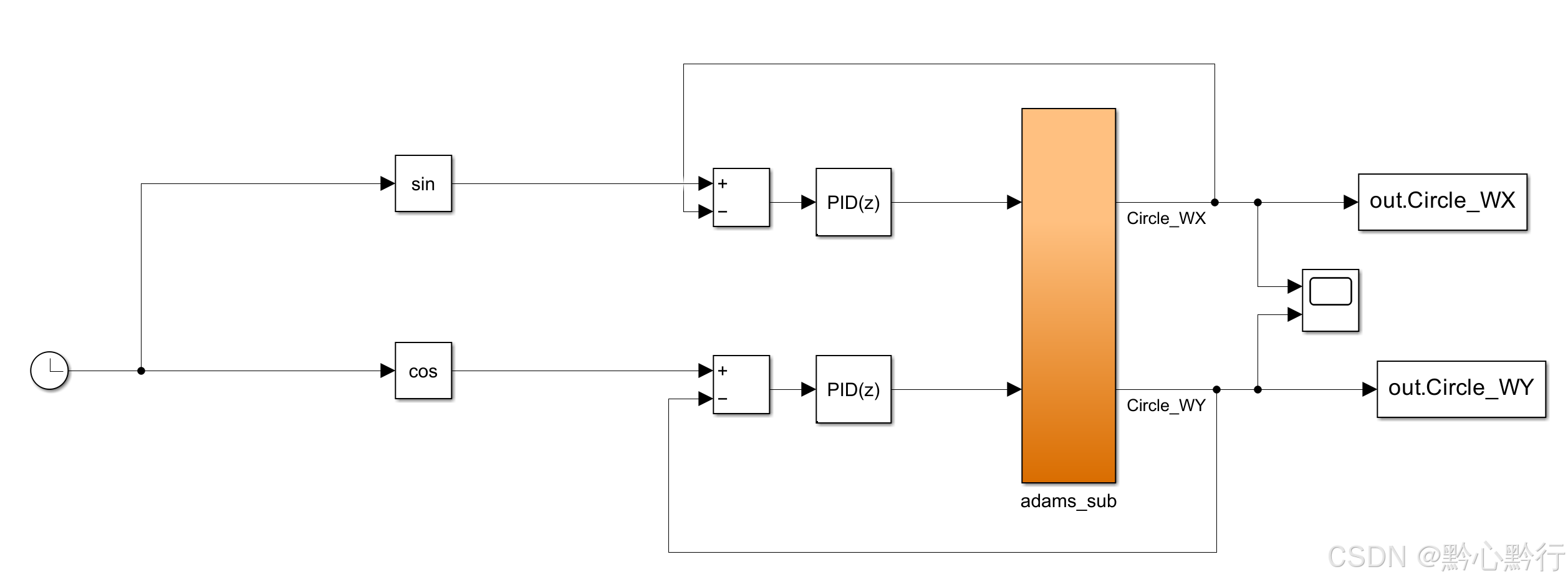
将X 和Y方向的位移组合绘制处小球4的运动轨迹：

轨迹绘图代码（这里限制坐标X和Y范围为-0.5到0.5了，如果有需要更改这力的值即可，或者直接删掉这一行）：

axis([-0.5 0.5 -0.5 0.5]);

% 计算圆的坐标 
circle_x = out.Circle_WX.Data;
circle_y = out.Circle_WY.Data;
circle_xtime = out.Circle_WX.Time;
circle_ytime = out.Circle_WY.Time;
tx = circle_xtime;
ty = circle_ytime;
x = circle_x; 
y = circle_y; 
% 在 MATLAB 图形窗口中绘制圆 
figure; plot(x, y); 
%小球在XY平面上的轨迹曲线
xlabel('X'); 
ylabel('Y'); 
title('圆的轨迹'); 
axis equal; 
axis([-0.5 0.5 -0.5 0.5]);
grid on;
clc;

如果需要查看Adams的运动动画，按下图进行操作即可：

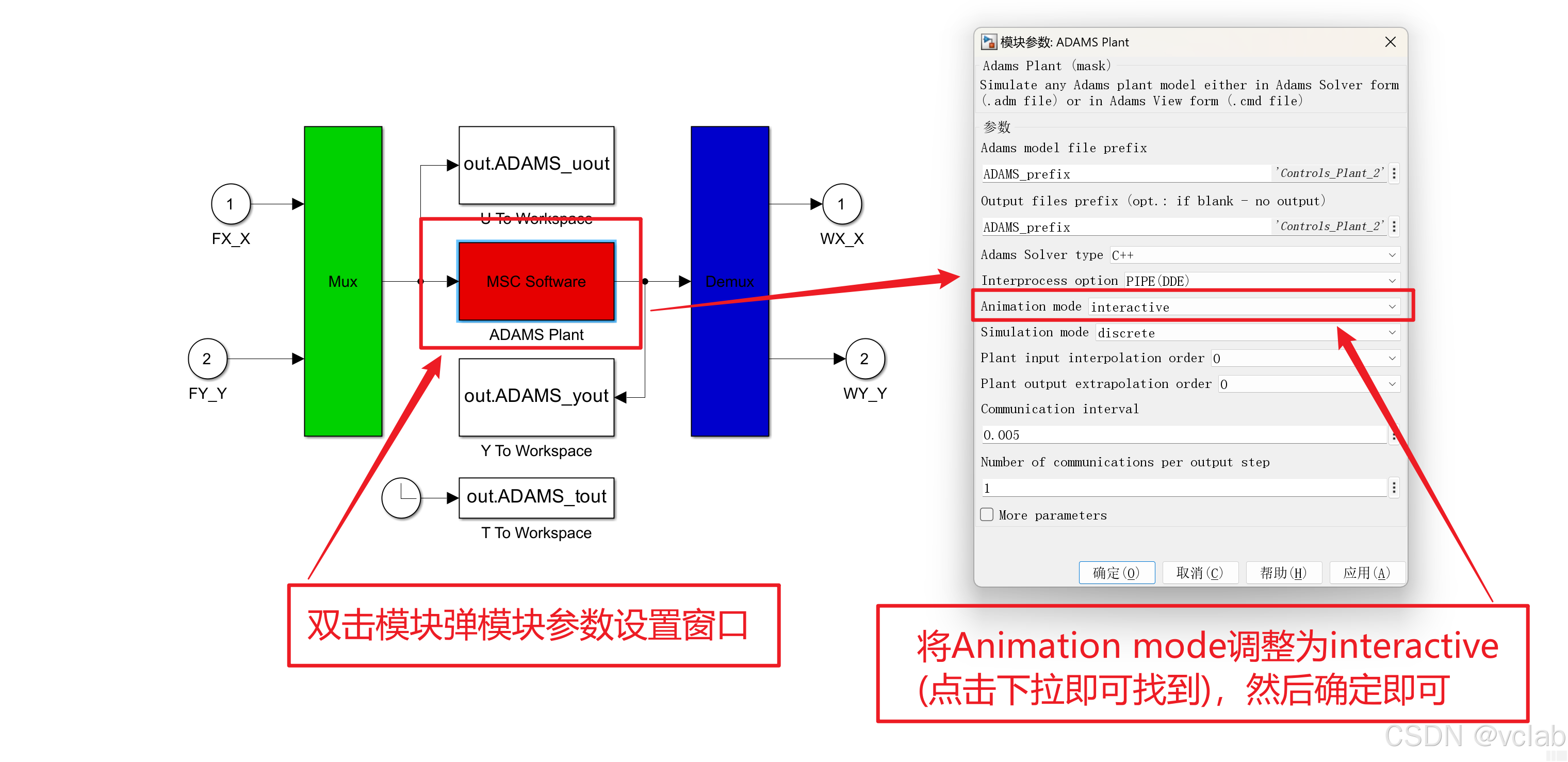
之后在Simulink中重新启动仿真，编译完成之后会弹出Adams的窗口，即可看到运动画面。

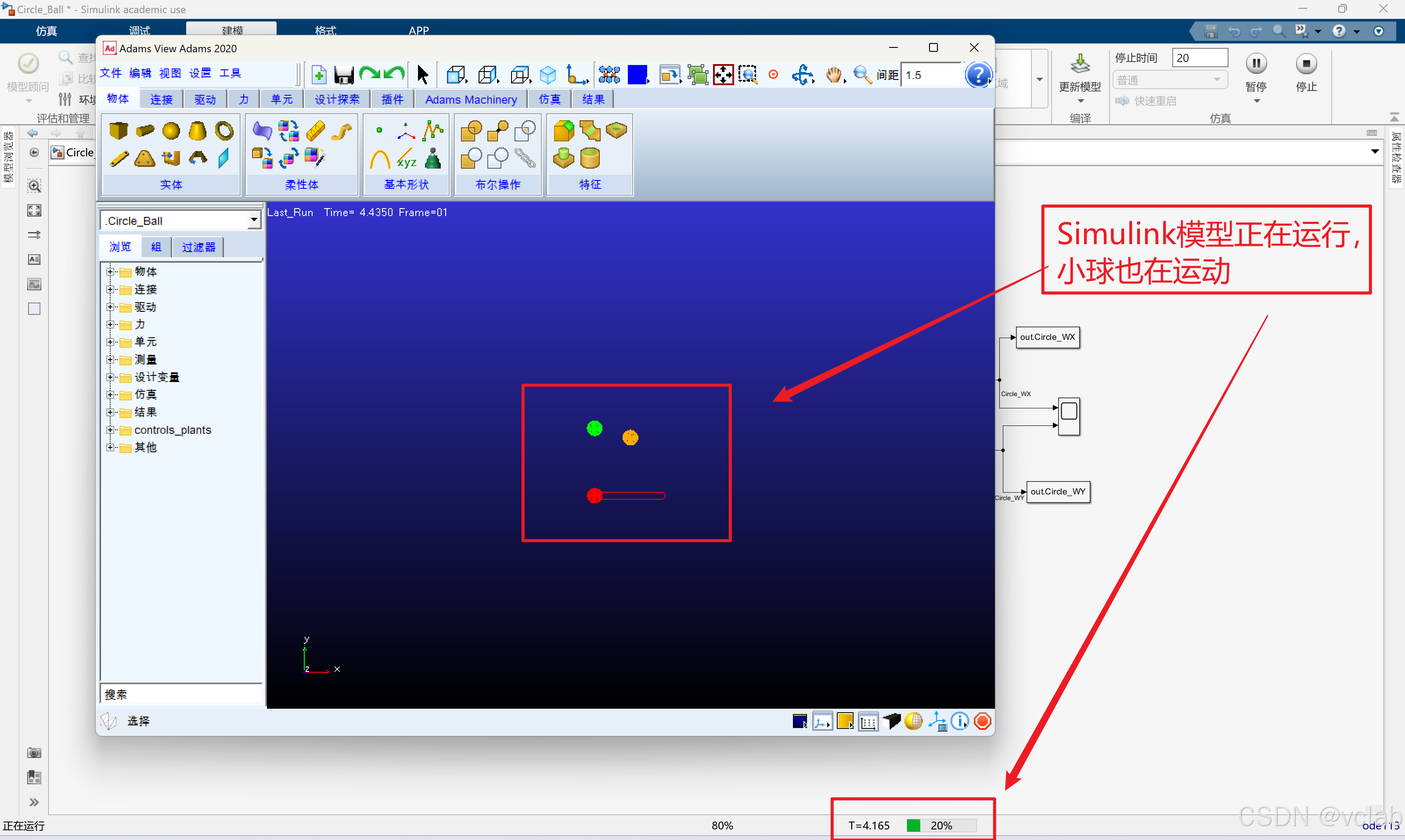
无论是matlab绘制运动轨迹还是在Adams中，圆心总体是朝着一个方向运动的，导致不是完

整的圆？这是为什么？

原因分析：即使是在变步长的情况，时间始终是离散的，所以在初始位移达到0.4时，加速度

ax不是瞬间变为0的，而是在很小一段时间内才变为0，线速度在这一短时间也是变化的，即其始终存在一个最小值（类似量子力学中的能量是一份一份的，其变化是跳跃性性的），导致时间是跳跃性变化，并不是连续变化，而力是时间的函数，因此力的变化也是跳跃性的，最终结果就是造成整个系统不是稳定的。

（3）问题解析

a. 解决方法

改成连续系统（理论分析），操作方法：

不过这种方式下，只能在Simulink中进行仿真，通过示波器或者轨迹作图查看结果，在Admas中即使打开交互窗口，小球也不会运动。结果如图所示，呈现完整的圆了。

四、解法二（闭环控制）

前面我们讲过直接控制施力的大小和方向来达到我们的目标轨迹，接下来，我们采用控制运动轨迹的方式来达到控制目的，其控制原理如下图所示，这里采用PID控制器。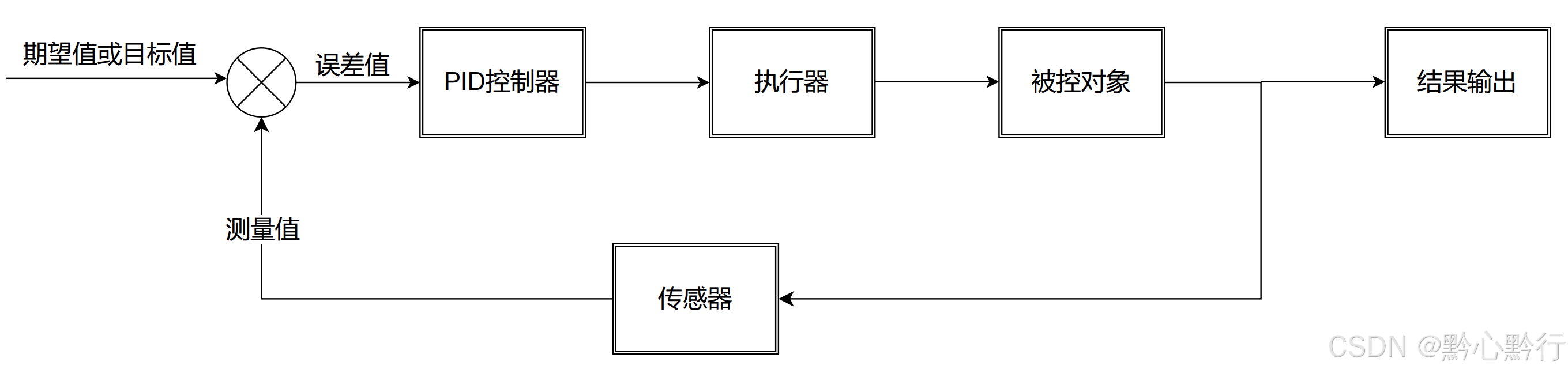

1、PID控制器

PID控制器即比例、积分、微分控制器，其原理图如下图所示。根据对P、I、D三个参数的不同整定方式分为普通PID、先进PID（神经网络、模糊控制、专家系统等）——推荐参考书籍《先进PID控制MATLAB仿真》—刘金琨。

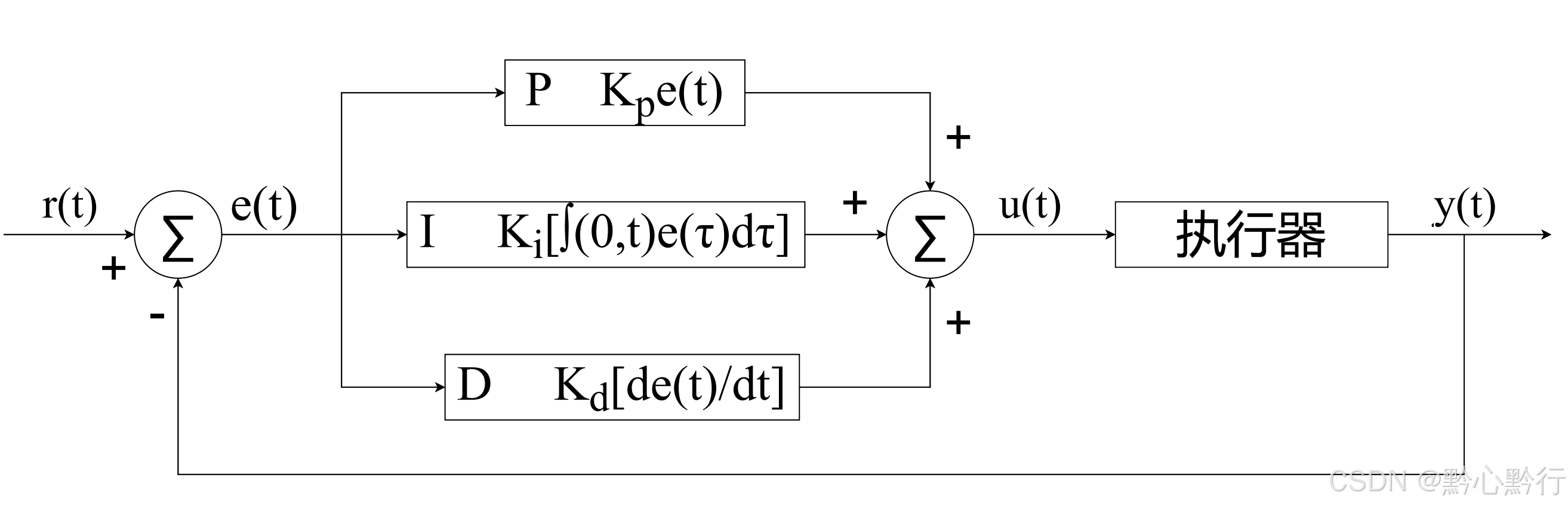
PID控制算法中，将目标值（目标曲线）作为输入，将输出与目标值进行比对，通过调整误差的大小来达到控制的目的，即当目标位移与实际位移相差较大时，通过减小或者增大作用力（或反向作用力）来控制位移的变化，使其与目标位置的误差达到最小。因此可以基于上述原理，使用simulink模型完成算法逻辑的搭建。

在simulink中可以基于PID原理手动搭建一个PID控制器，也可以直接采用自带的PID控制器，根据时间类型可分为离散型（左）和连续型（右）：

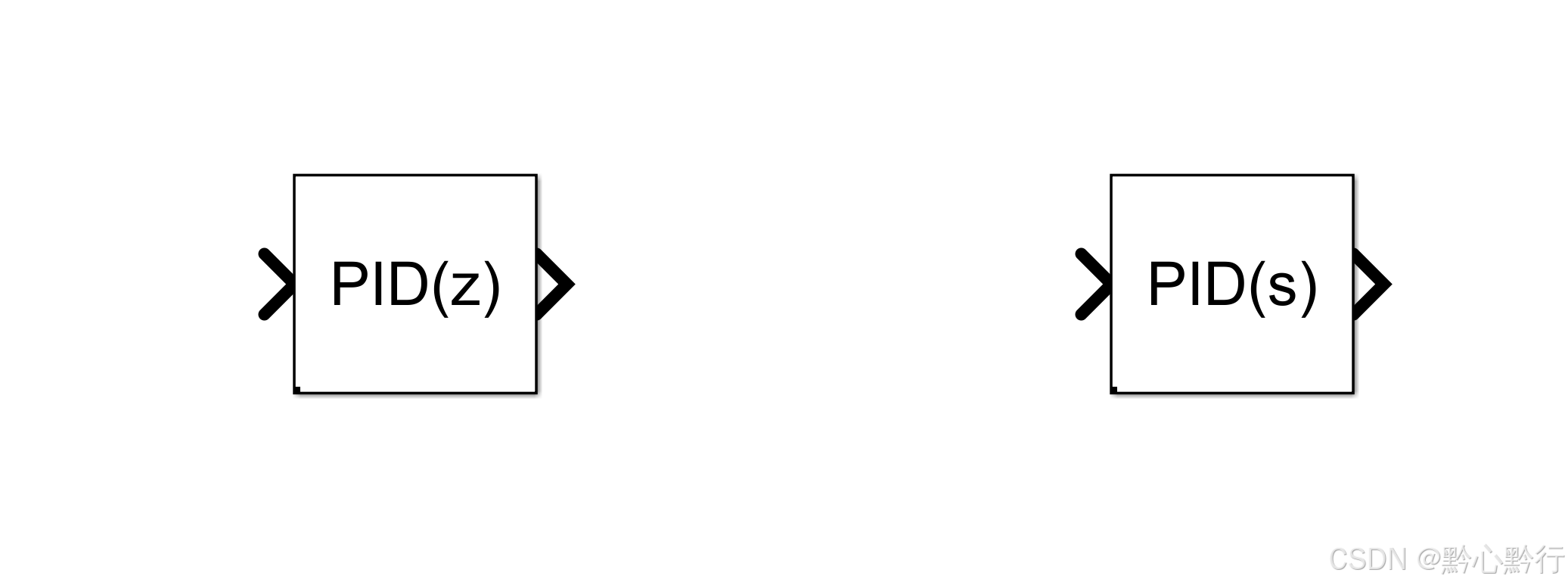
离散型和连续型PID控制器的设置界面

2、控制逻辑

小球在运动过程中主要受到X方向和Y方向的力，即两个输入量，输出为X和Y方向的位移曲线，也即两个输出量，即双输入输出的系统。但实际上X方向的力只控制X方向的位移，Y方向的力也只控制Y方向的位移，因此X方向和Y方向是独立。

（1）逻辑建模

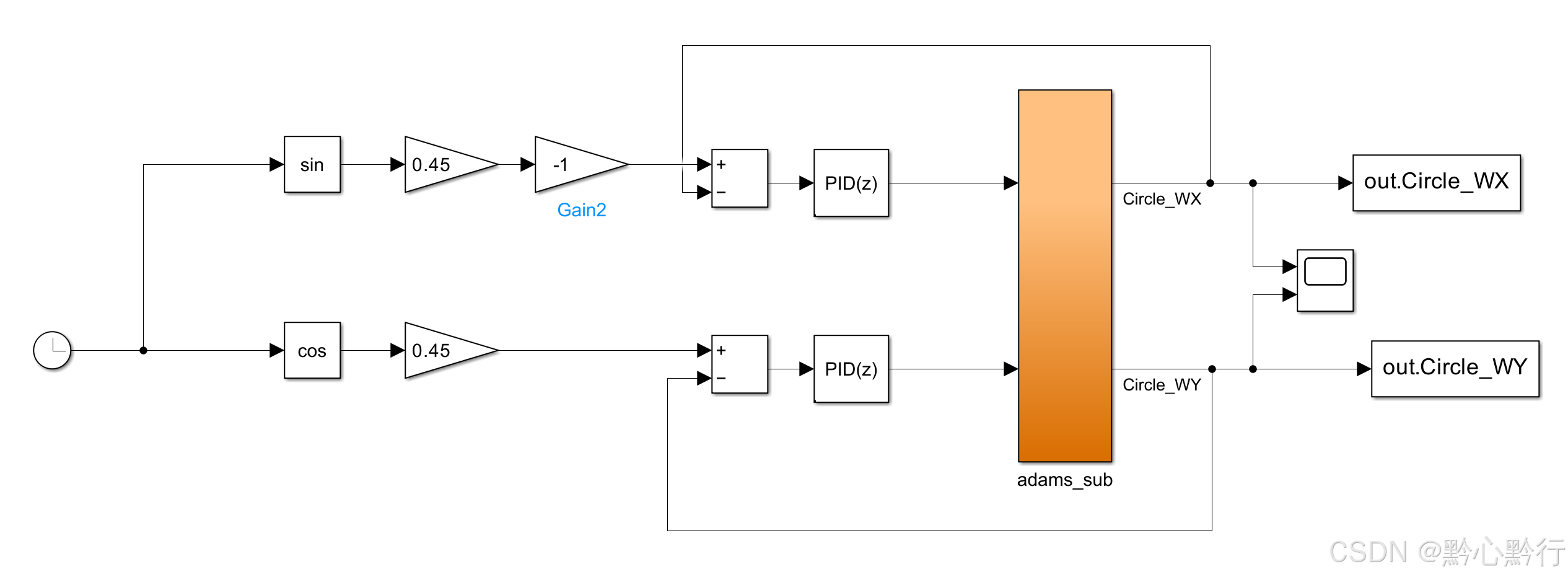
依据前面的分析，在整个系统中，我们只需要将X和Y方向对应的输入和输出进行关联即可，则simulink建模如下图所示：

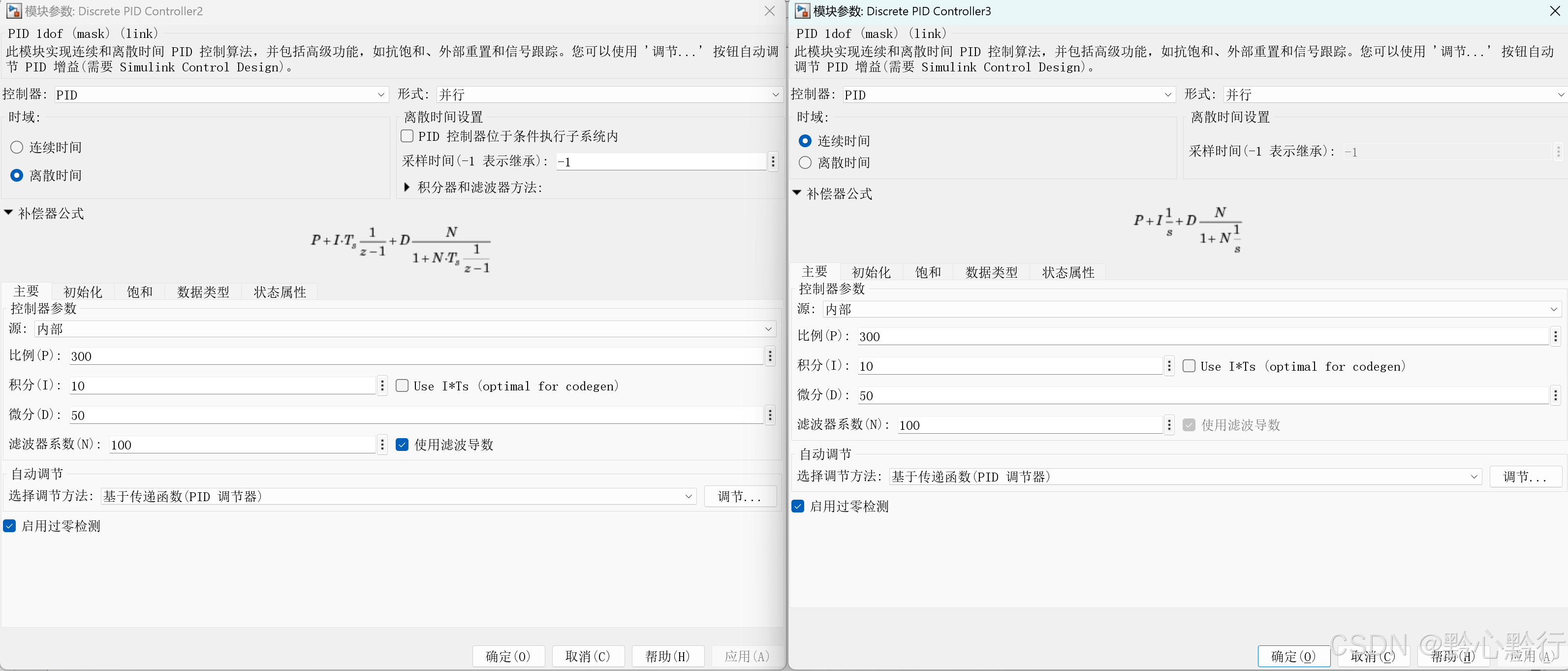
更改为离散型PID并设置PID参数为（两个PID参数相同）：

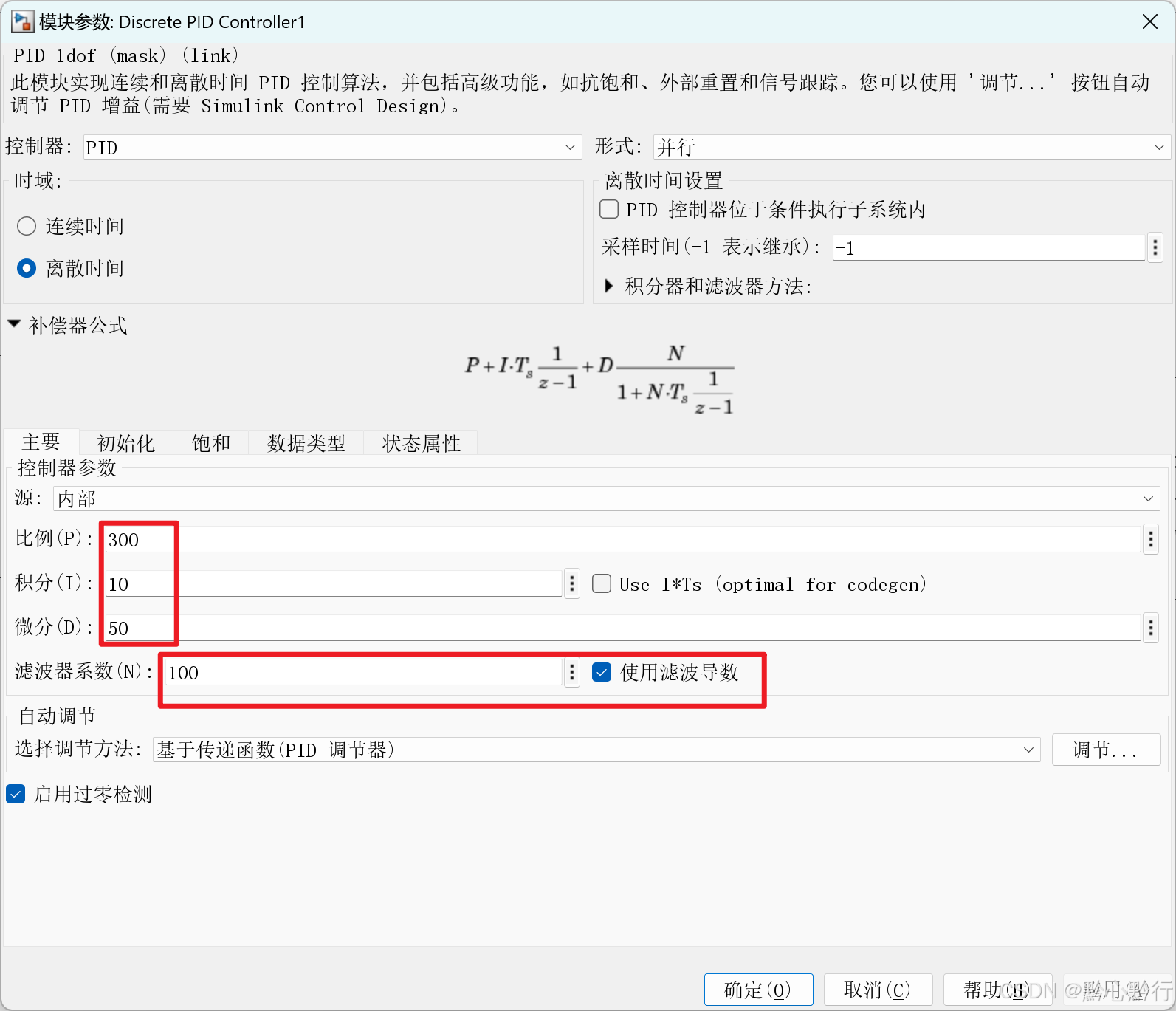
完成simulink建模后，打开Adams交互式仿真：

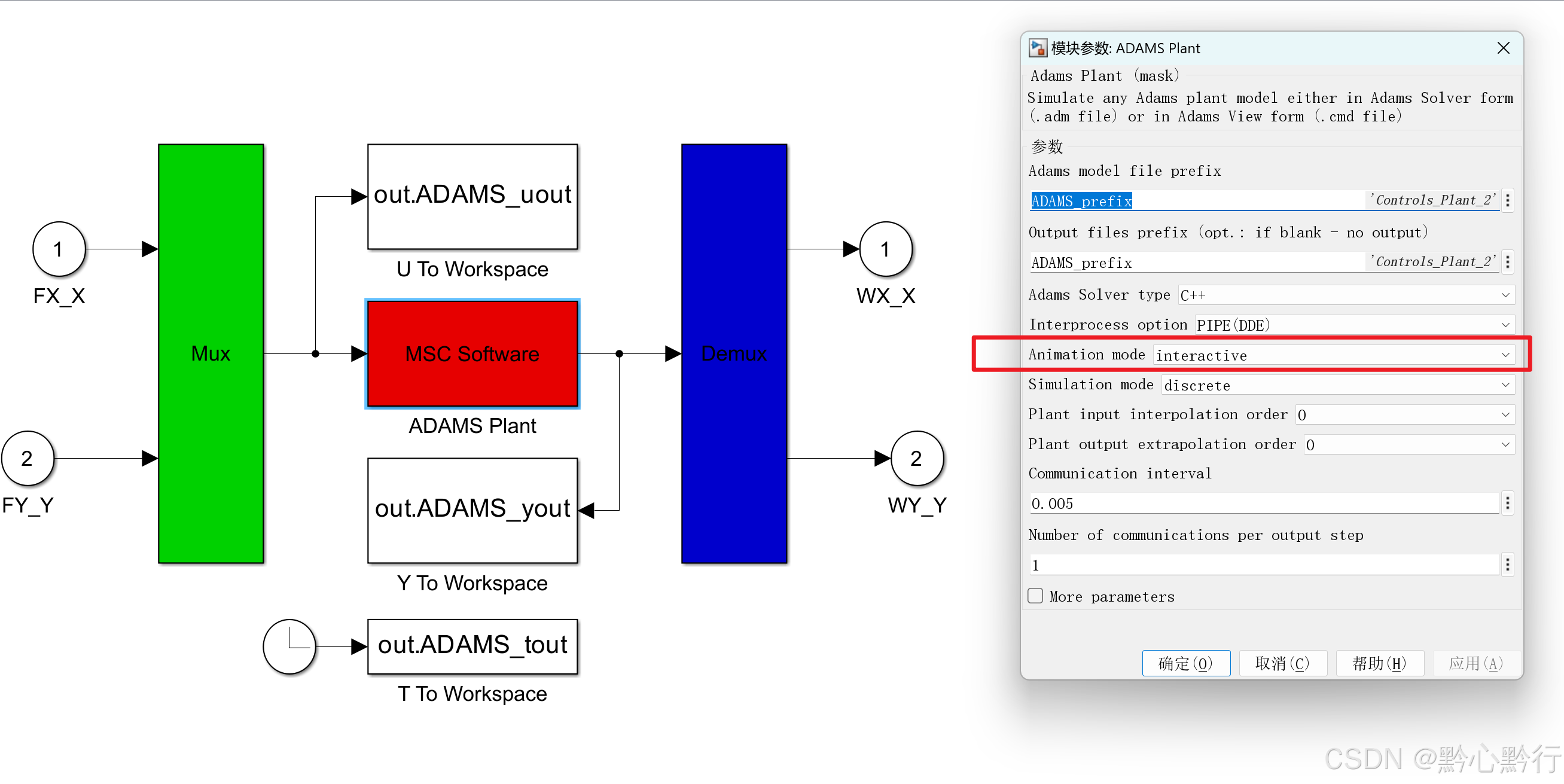
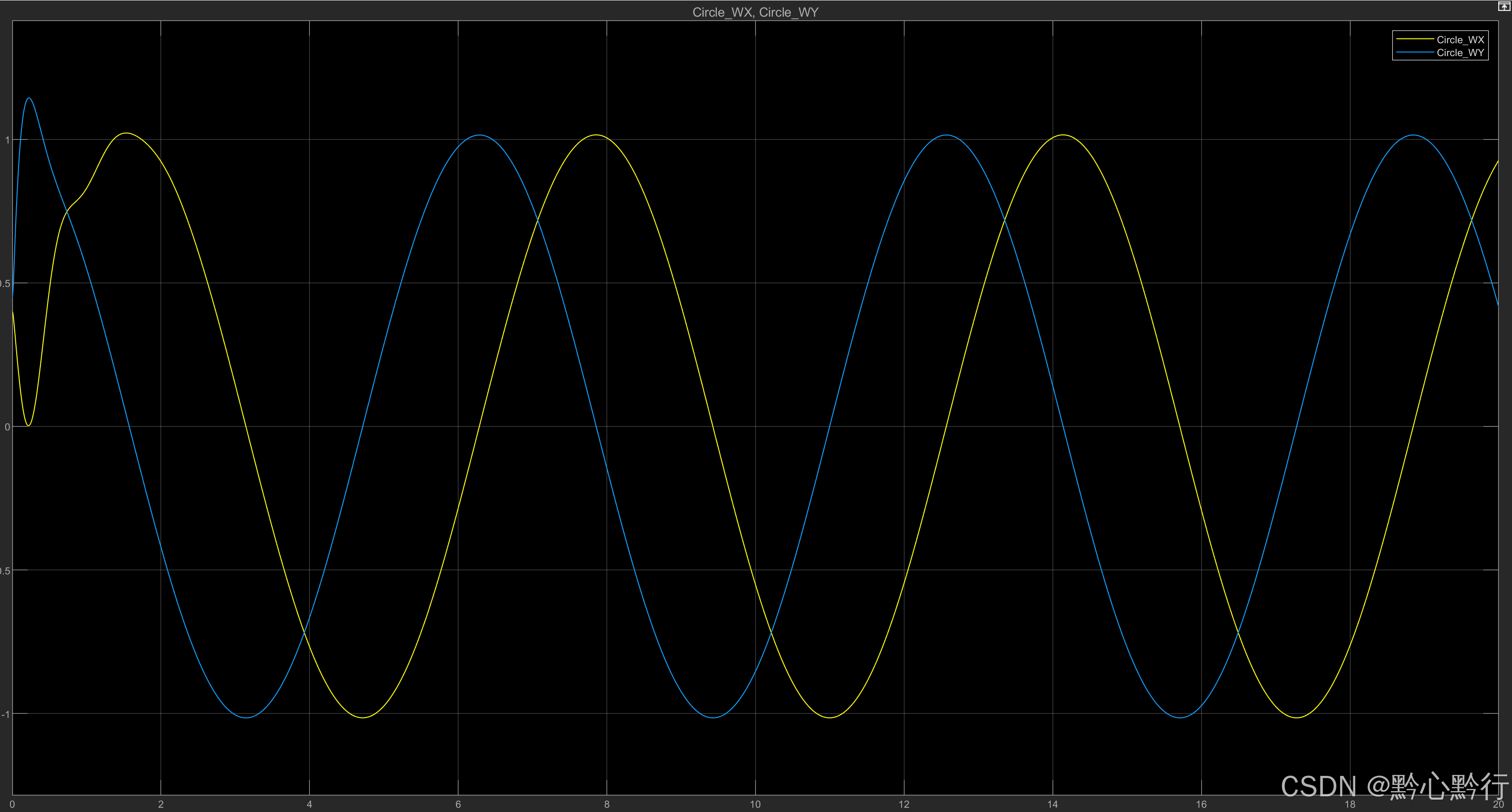
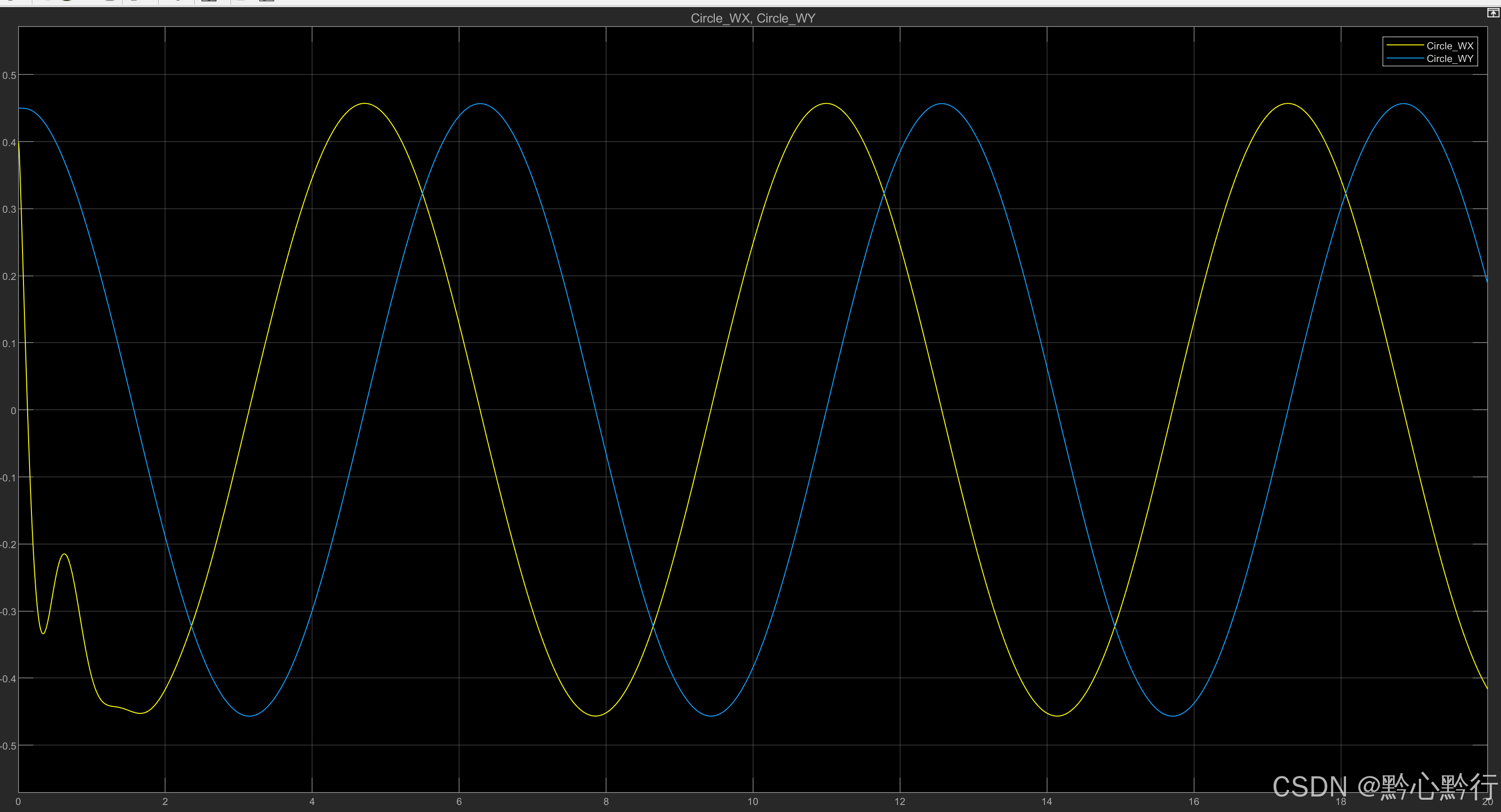
然后运行模型，可以看到运行动画，打开示波器，其X和Y方向的位移曲线如下：

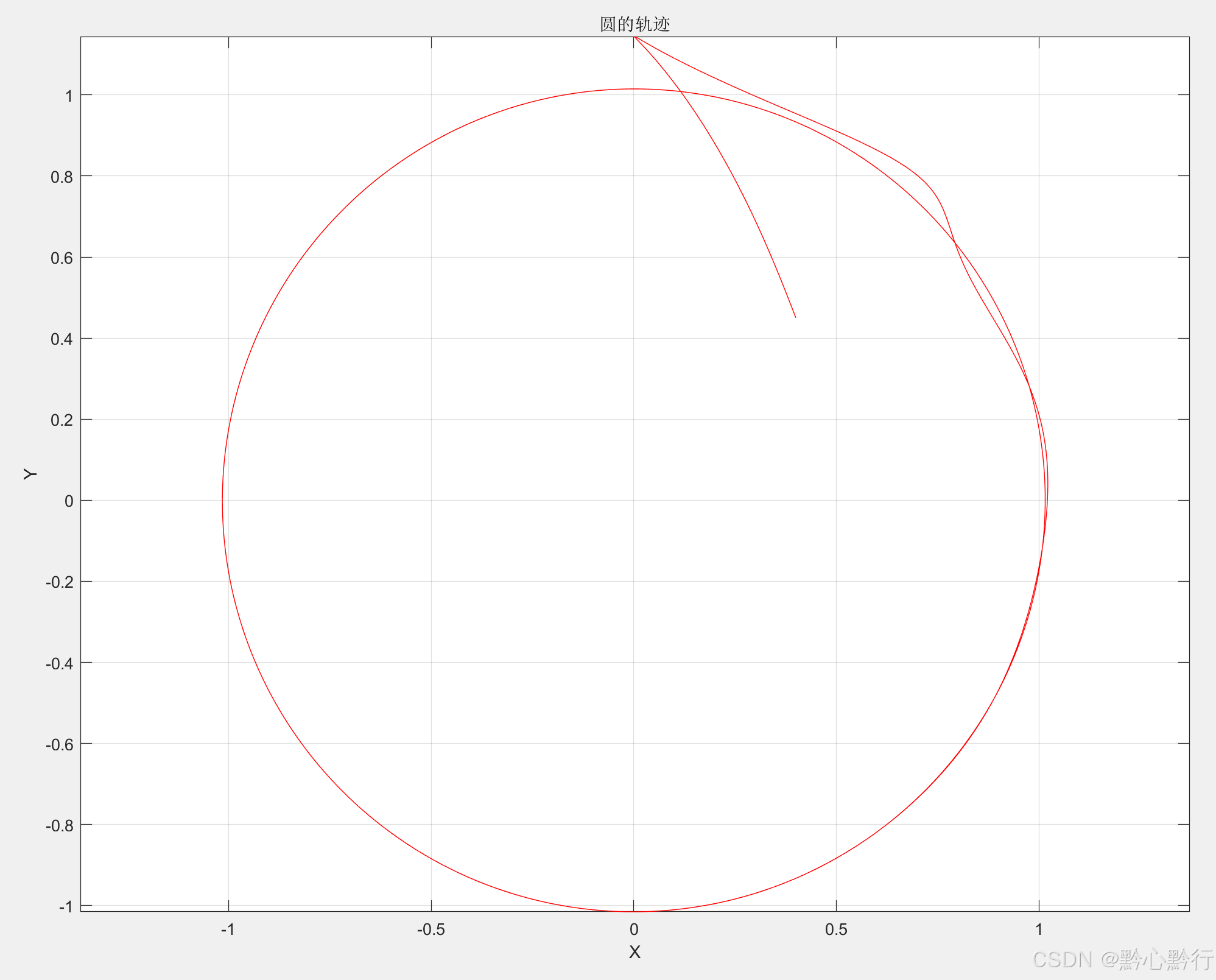
在matlab中运行轨迹绘制脚本代码（上一章第五节实现仿真中的轨迹脚本），得到轨迹曲线：

（2）逻辑优化

根据动画可知，其运行方向与第二章中的运行方向相反，根据轨迹以及位移曲线可知，其运行半径比第二章中的半径要大，因此还需要针对前面的控制逻辑进行优化。

A. 根据动画可知，其运动方向为顺时针，则可以将其中一个方向的位移进行反向控制（乘上负1）。

B. 上述逻辑中的三角函数的振幅为1，则其半径为1，只需要乘上一个目标振幅即可，第二章中的半径是0.45米，则乘上0.45。

则优化后的逻辑如下：

位移曲线：

轨迹图：

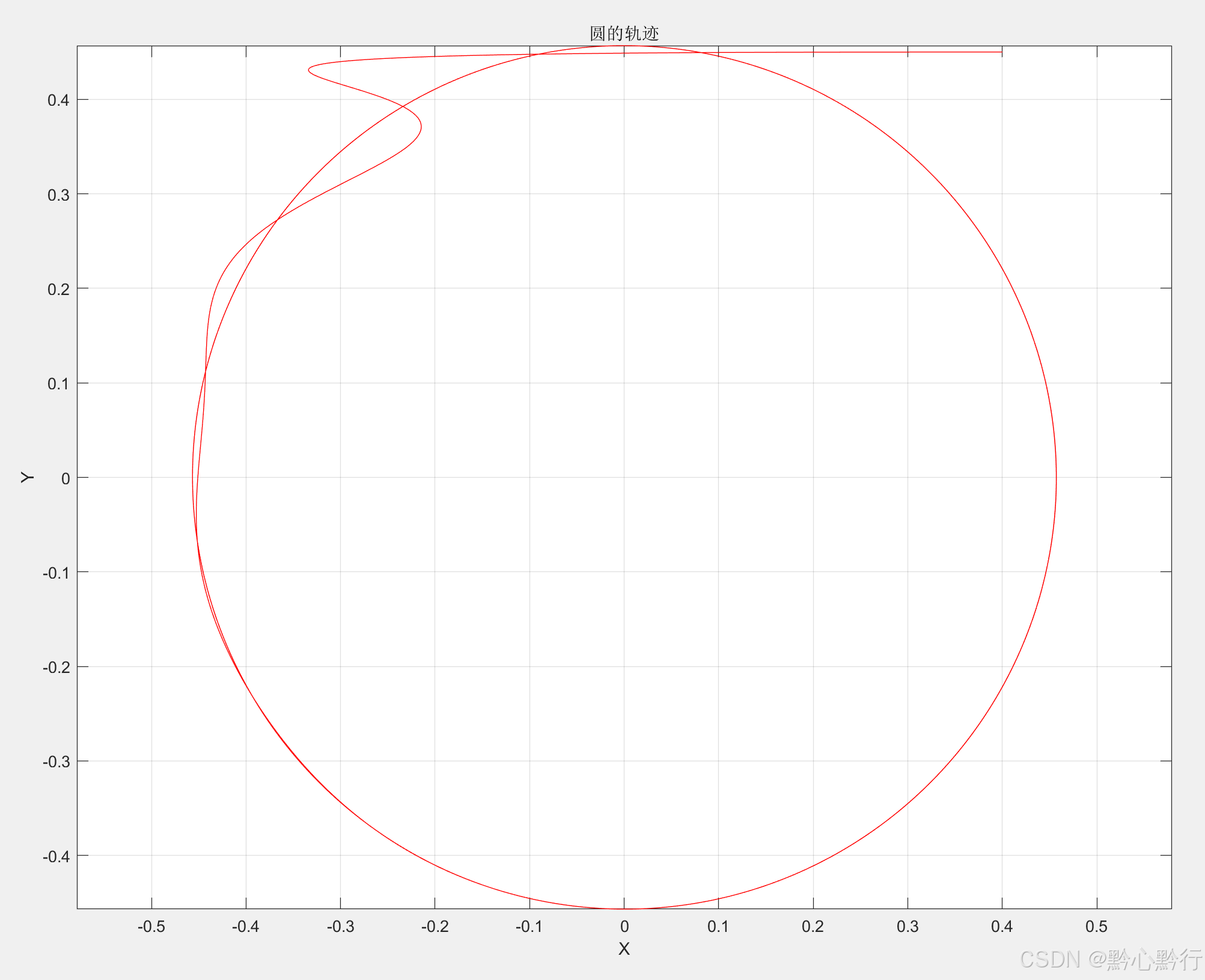
无论从动画、还是轨迹半径，基本上与上一章中的相似了，说明逻辑可行。

3.拓展

基于上一节中的算法优化，我们可以控制半径、运动方向，那是不是也可以控制运动圆心呢，当然可以。比如就以现在小球所在位置为圆心做圆周运动，按照圆的方程组：

$(x+a)^{2}+(y+b)^{2}=R^{2}$

则只需要在对应轨迹上加上圆心的坐标值即可，则建模如下：

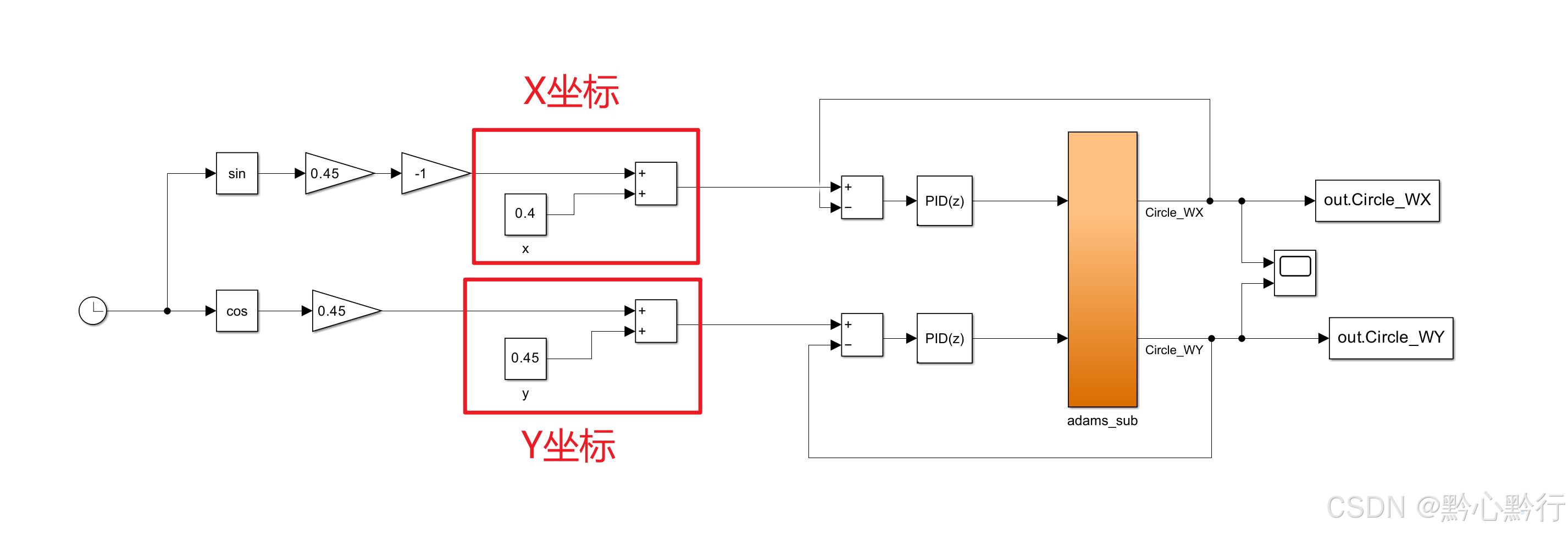
轨迹如下图所示：

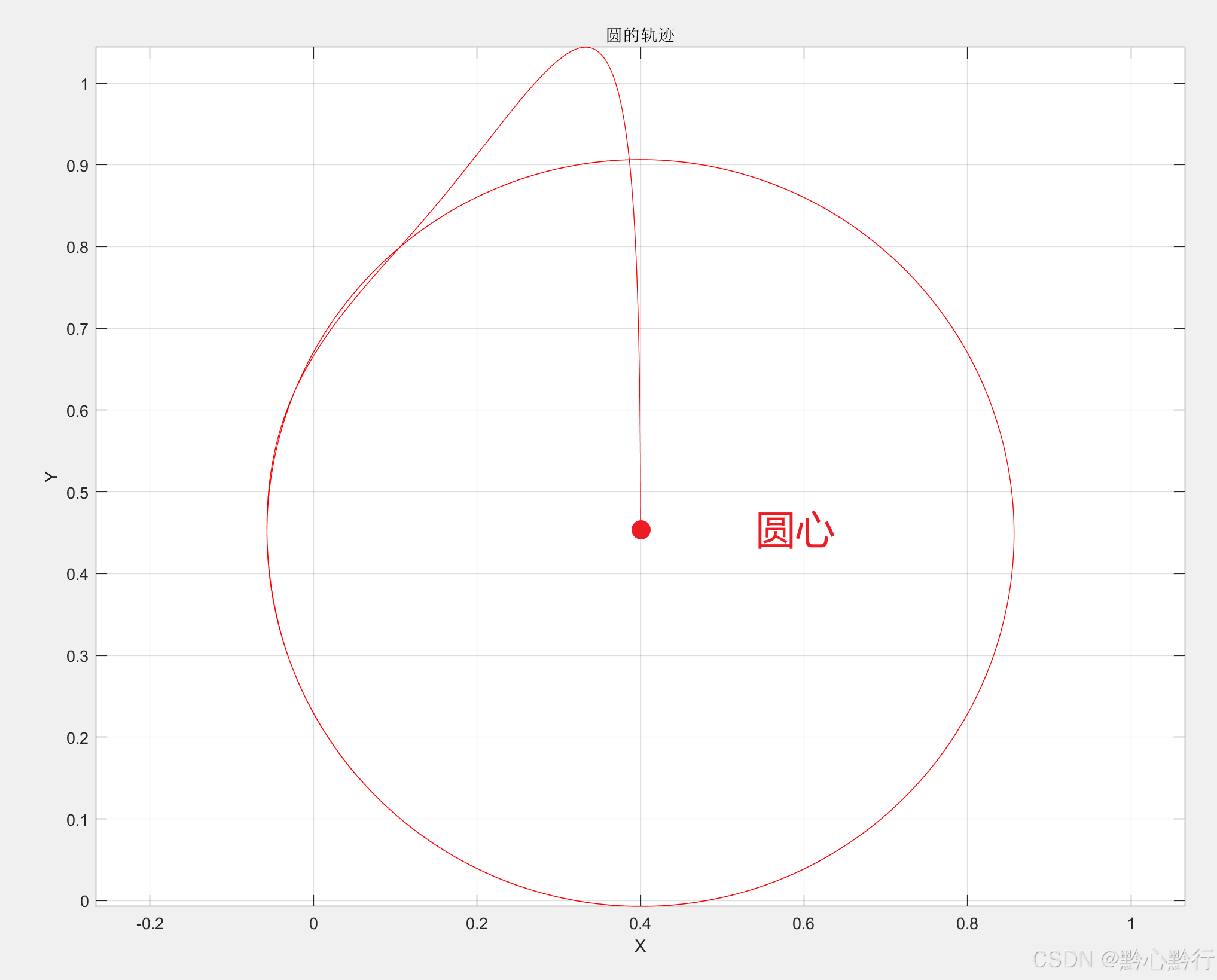
同理，根据前面调整半径的方式，可以设计成螺旋运动，即半径逐渐增大，只需要乘上一个随时间变化的函数即可，建模如下：

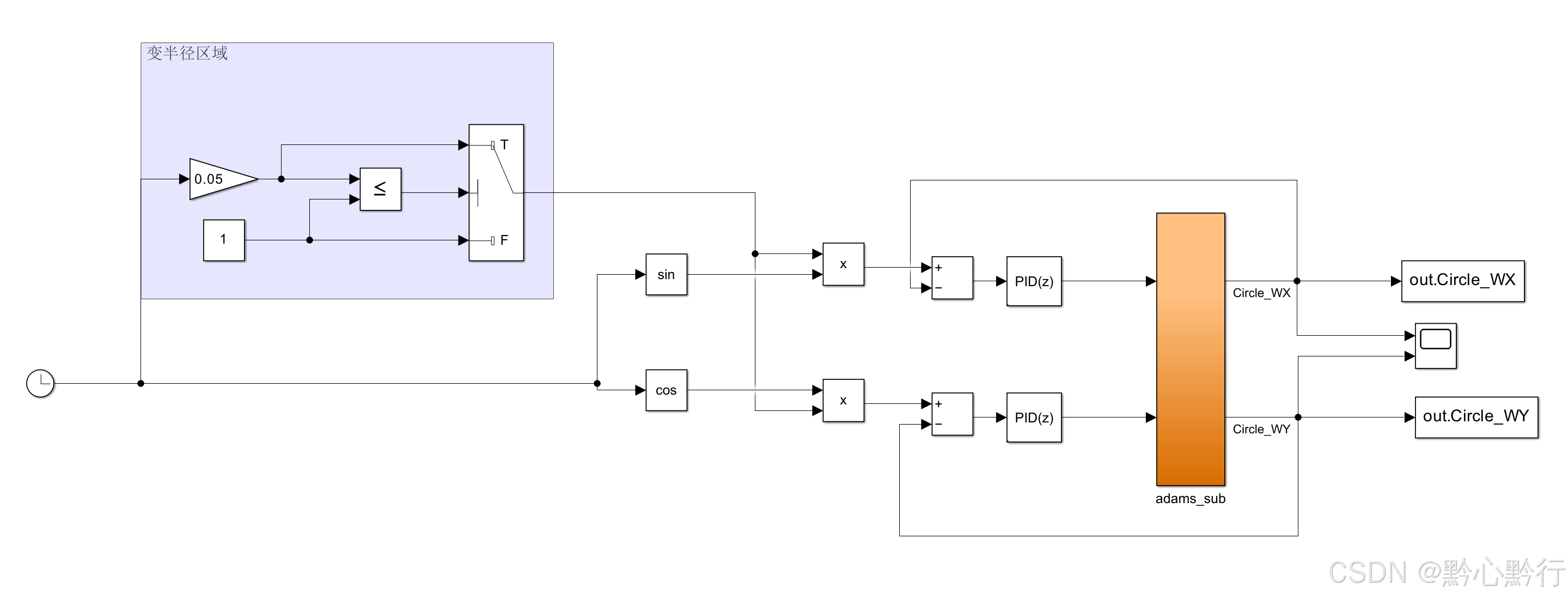
运动轨迹：

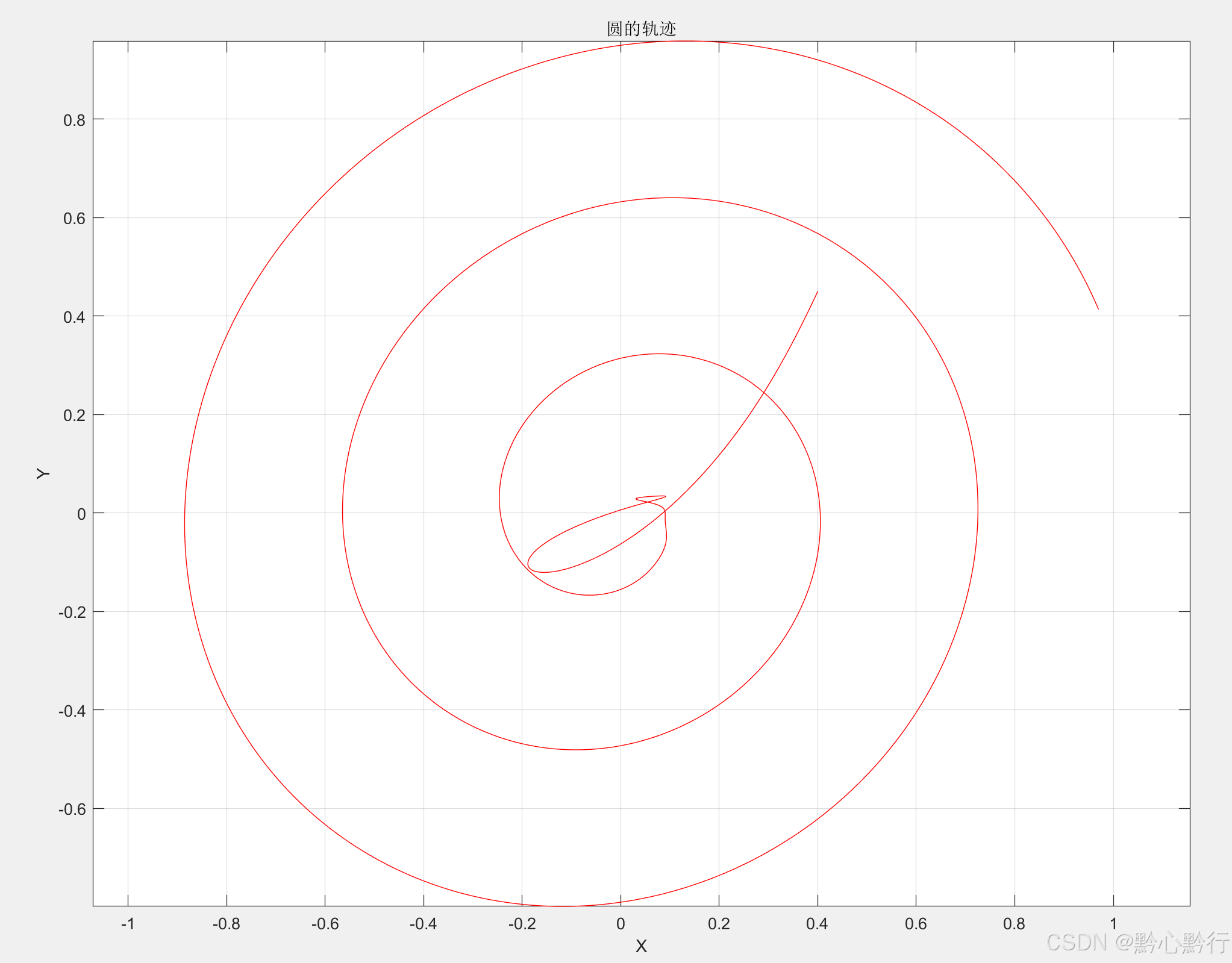
除了在平面上，也可以增加Z轴方向的控制，实现空间上的运动控制，大家可以自行尝试，与本文中内容原理相通。

综上，采用PID的情况下，可以实现变半径或者变圆心的运动控制，甚至两者的结合运动。相对于上一章中的控制方法会更加便捷。但在整个PID控制过程中无论是动画、曲线还是轨迹图都可以看到其在初始阶段都会出现异常情况，这主要是和PID参数有关，这里所提供的PID参数仅能展示大体的运动情况，并不是最优的参数。

不合适的参数会导致过冲、达到稳态时间拉长等。但手动调整参数是一个乏味且漫长的过程，需要一定的经验基础、或者采用更先进的整定方式，比如通过其他算法来调整PID的P、I、D三个参数来实现最优解，设计知识盲区，待我学成归来再分享给大家。

总结

这是一个学习过程中的记录，总体上在于熟悉adams和matlab的联合仿真，同时了解PID控制原理。但过程中也存在很多问题，如圆心移动、初始阶段异常等。一部分是可以通过算法解决，另一部分则无法解决。

在下一篇中则采用其他方式实现Adams和Simulnk的联合仿真：前面是将Adams模型导入Simulink中，在查看运行动画时无法在Adams中进行控制。而接下来将实现Simulink算法导入Adams软件中去，大家可以期待一下。