【C++】刷题汇总(day15)--平方数、分组、拓扑排序-优快云博客

#include<iostream>
#include<math.h>
using namespace std;

int main()
{
    long long x  = 0;
    cin >>x;
    long long y  = sqrt(x);
    
    if( x - y*y < (y+1)*(y+1)-x)
        cout << y*y << endl;
    else cout << (y+1)*(y+1) <<endl;
    
    return 0;
}

2、分组

2.1 题目

2.2 思路

读完题，知道让处理可能实际应用场景的分组情况，其中n个同学分为m组，需满足条件1每一组里的同学都必须擅长同一个声部，还需要满足条件2不同组同学擅长同一个声部的情况是可以出现的，还需要满足条件3不希望出现任何一组的人过多，最后需要满足条件4人数最多的小组的人尽可能少，如果无法顺利安排，则输出-1即可。

以示例1为例，n为5，m为3，然后 2，2，3，3，3表示各个同学擅长的声部，划分可以有多种情况，但是在满足以上情况下的满足条件的划分形式就是2 ，2，1表示每个组的人数，且需满足声部相同的分一起如第一组22，第二组33，第三组3，那么输出最多小组的人数为2即可。再比如，划分不能以不同声部如2,3一组，不满足条件1。理解题意后，进行分析思考，要满足以上条件且最后输出最多组人数，那么尝试暴力枚举，直接从⼩到⼤枚举所有可能的最⼤值，找到第⼀个符合要求的最⼤值。那么为了方便理解画个图推导：

根据上图推导演算，继续假设最终最多人数小组人数为x，分析总结：
(1)、分析举例多组数据，得到人数与组数之间的关系式：m = n/x + n%x==0 ? 0 : 1；表示最多⼈数为 x 时，能分成 m 组.注意此时的m不等于输入的m，而是利用每组m的和与输入的m作比较。
(2)、除此外需要满足以上4个条件。
所以综上所述，得出实现过程需要以下几个条件分为：

利用哈希表hashcount统计每种声部的⼈数；如i声部a个人，2声部b个人等等。
遍历哈希表hashcount求出声部最多的⼈数hashmax，表示
再判断hashcount组数，处理边界情况;如输入n=5,m=3,但是输入声部情况x.first为1，2，3，4,2这种情况将会分为4组，4>m不满足条件1，同一声部必须擅长同一声部。
最后采用蛮力法从小到达枚举所有情况，直到找到第⼀个符合要求的最大人数即可。

所以第一步，先按照题目要求写好输入n和m，再顺便利用哈希hashcount统计好每种声部的⼈数;然后再次遍历hashcount求出最大人数hashmax.

2.3 代码实现

2.3.1 暴力枚举

#include<iostream>
#include<unordered_map>
using namespace std;
int n,m;
unordered_map<int,int> count;

bool check(int x)
{
    int g = 0;
    for(auto& [a,b] : count)
    {
        g += b/x + (b%x == 0 ? 0 : 1);
    }
    return g <= m;
}
    
int main()
{
    cin >> n >> m;
    int hmax = 0;
    for(int i = 0;i < n;i++)
    {
       int x = 0;
        cin >> x;
        hmax  = max(hmax,++count[x]);
    }
    int k = count.size();
    if(k > m)
        cout << -1 << endl;
    else
    {
        for(int i = 1;i <= hmax;i++)
        {
            if(check(i))
            {
                cout << i << endl;
                break;
            }
        }
    }
    
    return 0;
}

2.3.2 二分

虽然暴力解法能过，但是时间复杂度还是有点高的，所以，基于之前做过的二分法思想，可以对其暴力法进行优化

因为对于人数很大的情况下，从人数[1,hashmax]不难看出，1个人一组肯定无法满足所有条件，依次类推2，3等等，所以会发现将区间进一步划分为[1,mid），[mid,hashmax]时，前区间[1,mid]情况时，总会check() > m，所以干脆如此就利用二分法，进行优化处理。那么，我们在暴力解法基础上，再加一层判断，如果check(mid) < m则更新mid，否则边界对半

#include<iostream>
#include<unordered_map>
using namespace std;
int n,m;
unordered_map<int,int> count;

bool check(int x)
{
    int g = 0;
    for(auto& [a,b] : count)
    {
        g += b/x + (b%x == 0 ? 0 : 1);
    }
    return g <= m;
}
    
int main()
{
    cin >> n >> m;
    int hmax = 0;
    for(int i = 0;i < n;i++)
    {
       int x = 0;
        cin >> x;
        hmax  = max(hmax,++count[x]);
    }
    int k = count.size();
    if(k > m)
        cout << -1 << endl;
    else
    {
        int l = 1,r = hmax;
        while(l < r)
        {
            int mid = (l+r)/2;
            if(check(mid)) 
                r = mid;
            else l = mid + 1;
        }
        cout << l << endl;
    }
    
    return 0;
}

3、拓扑排序

3.1 题目

3.2 思路

读完题，知道属于是数据结构图论知识，判断输入数据和序列是否满足拓扑图，满足输出序列，不满足输出-1即可。为了方便理解画个图：

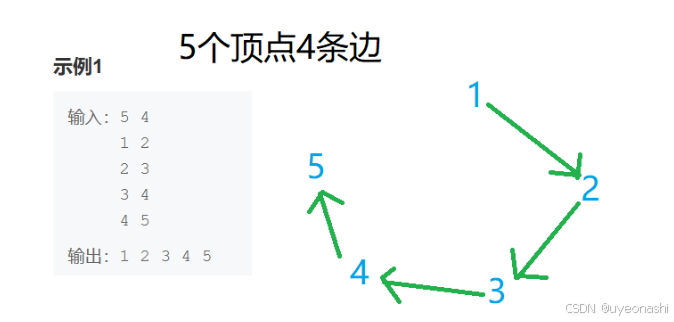
3.3 代码实现

首先，按照题目要求输入数据，并且同时存储u顶点与v边的信息，以及累计每个顶点的入度数，接着将入度为0的入队列，再执行步骤三，不为空就出队列，记录被消除的顶点尾插到ret中，方便输出，执行完队列操作后，判断size是否等于n，相等说明成功实现完全消除，否则就是不满足拓扑序列。输出-1即可。值得注意的是此题提交的测评会计入最后一个字符后是否带空格的情况，所以最后一个顶点单独输出处理即可。

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 2e5 + 10;
//邻接链表
vector<vector<int>> edges(N);// edges[i]表示i顶点的边的关系
int indegree[N];// 统计⼊度信息

queue<int> q;
vector<int> ret; // 记录最终结果 

int main()
{
    int n,m;
    cin >> n >> m;
    while(m--)
    {
        int u,v;
        cin >> u >> v;
        edges[u].push_back(v);// 存储u顶点与v边的信息
        indegree[v]++;// 存储累计各顶点的⼊度 

    }
    // 把⼊度为 0 的点放进队列中
    for(int i = 1; i <= n; i++)  
    {
        if(indegree[i] == 0)
        {
            q.push(i);
        }
    }
    // 执行队列操作
    while(q.size())
    {
        int a = q.front();
        q.pop();
        ret.push_back(a);
        for(auto b : edges[a])
        {
            if(--indegree[b] == 0)//同时处理度数和判断度数
            {
                q.push(b);
            }
        }
    }

    // 判断 
    if(ret.size() == n)
    {
        for(int i = 0; i < n - 1; i++)
        {
            cout << ret[i] << " ";
        }
        cout << ret[n - 1]; // 测评会考虑最后⼀个元素的空格 
    }
    else
    {
        cout << -1 << endl;
    }
    return 0;
}