LDL组会论文分享

Label Enhancement with Sample Correlations via Low-Rank Representation 论文分享

method

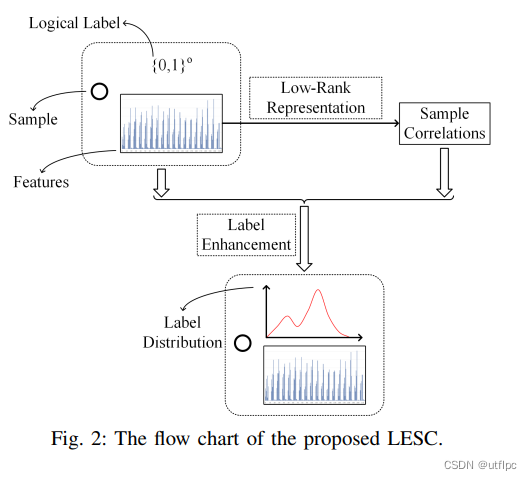
采用低秩表示方法（low-rank representation）来捕获样本的全局关系并预测隐式标签相关性以实现标签增强。

motivation

• 基于部分的每个实例的图构建过程中仅利用了局部拓扑特征，而特征空间的整体信息还没有得到很大的利用。
• 方法需要超参数的先验知识

期望一种全局挖掘整个特征空间的全局结构并对参数具有鲁棒性的方法

具体做法

low-rank representation（LRR）对数据子空间表示施加低秩约束以捕获所有实例的全局关系。
构建的低秩结构通常可以平滑地转移到标签空间，所以利用特征空间的最低秩表示来表示标签分布的LRR。
将获得的 LRR 合并到目标函数中，以探索标签分布空间中的隐藏线索。

notations

$X=[x_1;x_2;...x_n]$	feature matrix
$\Gamma =[L_1;L_2;...L_n]$	logical label matrix
$\mathfrak{D}=[D_1;D_2;...D_n]$	label distribution matrix

mapping model

对于实例$x_i$,其标签分布为$$D_i=\varphi (\hat{\theta },\xi (x_i)).$$
$\varphi (\hat{\theta },\cdot )$表示由 $\hat{\theta }$ 参数化的线性变换.
$\xi (x_i)$表示高斯核函数将$x_i$（也就是特征）映射到高维空间中

$\hat{\theta }$的最优化

$$\underset{\hat{\theta }}{\min }\mathcal{L}(\hat{\theta })+{\lambda }_1\Psi (\hat{\theta })$$
$\mathcal{L}(\hat{\theta })$代表损失函数
$\Psi (\hat{\theta })$是挖掘原始特征空间中信息和标签之间的相关性的函数

损失函数

The least-squares (LS) loss function：
$$\mathcal{L}(\hat{\theta })=\sum _{i=1}^n\Vert \varphi (\hat{\theta },\xi (x_i))-L_i\Vert$$

挖掘函数

在LRR中，所有样本及其全局关系都由少量数据的线性组合表示，在一般情况下，该属性可以转移到标签空间。
因此，可以得到标签分布$\mathfrak{D}$的低秩恢复，即找到一个合适的$\mathfrak{D}$，使$\mathfrak{D}$与$\mathfrak{D}\hat{C}$的距离最小，其中$\hat{C}$是特征空间的最小LRR。
$$\Psi (\hat{\theta })=\Vert \mathfrak{D}-\mathfrak{D}\hat{C}{\Vert }_F^2=\Vert (I-{\hat{C}}^T){\mathfrak{D}}^T{\Vert }_F^2$$

$\hat{C}$的最优化

在特征矩阵中寻找LRR来挖掘特征空间的全局结构，即假设$X=XC+E$，然后解决以下正则化秩最小化问题:
$$\underset{C,E}{\min }rank(C)+{\lambda }_2\Vert E{\Vert }_l,s.t.,X=XC+E$$
$E$是 the sample-specific corruptions.

为计算方便，秩函数用核范数代替：
$$\underset{C,E}{\min }\Vert C{\Vert }_{\ast }+{\lambda }_2\Vert E{\Vert }_{2,1},s.t.,X=XC+E$$

向量范数与矩阵范数

目标函数

$$\begin{gathered} P\left(\hat{\theta }\right)=\sum _{i=1}^n\Vert \varphi (\hat{\theta },\xi (x_i))-L_i\Vert +{\lambda }_1\Vert (I-{\hat{C}}^T){\mathfrak{D}}^T{\Vert }_F^2 \\ =tr\left[\right(\varphi (\hat{\theta },\Xi ),-\Gamma {)}^T(\varphi (\hat{\theta },\Xi ),-\Gamma )] \\ +{\lambda }_{1}tr(\mathfrak{D}(I-\hat{C})(I-\widehat{C^T}){\mathfrak{D}}^T\left)\right) \end{gathered}$$

$\Xi =[\xi (x_1),...,\xi (x_n)].$

矩阵F范数的平方转化为矩阵的迹

矩阵范数与向量范数的公式及其理解