2023/8/6周报 反向传播和损失函数

摘要

反向传播算法，简称BP算法，适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。BP网络的输入输出关系实质上是一种映射关系：一个n输入m输出的BP神经网络所完成的功能是从n维欧氏空间向m维欧氏空间中一有限域的连续映射，这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合，因此具有很强的函数复现能力。这是BP算法得以应用的基础。

Abstract

Backpropagation, referred to as BP algorithm, is a learning algorithm suitable for multi-layer neural networks. It is based on the Gradient descent. The input-output relationship of BP network is essentially a mapping relationship: the function of a BP neural network with n inputs and m outputs is the continuous mapping from n-dimensional Euclidean space to a Finite field in m-dimensional Euclidean space, which is highly nonlinear. Its information processing ability comes from the multiple composite of simple nonlinear functions, therefore it has strong function reproduction ability. This is the foundation for the application of the BP algorithm.

反向传播

背景：
BP网络的学习过程是一种误差修正型学习算法，由正向传播和反向传播组成。在正向传播过程中，输入信号从输入层通过作用函数后，逐层向隐含层，输出层传播，如果在输出层得不到期望的输出，则转入反向传播，逐层求出目标函数对各神经元权值的偏导数，构成目标函数对权值向量的梯度，作为修改权值的依据，网络的学习在权值修改过程中完成。输出值与真实值的误差达到所期望值时，网络学习结束。

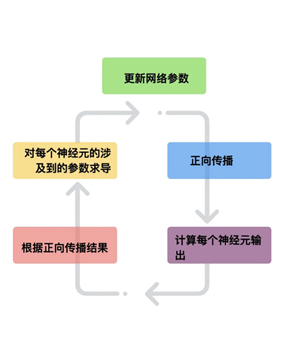
下面举例说明反向传播的实施方法：

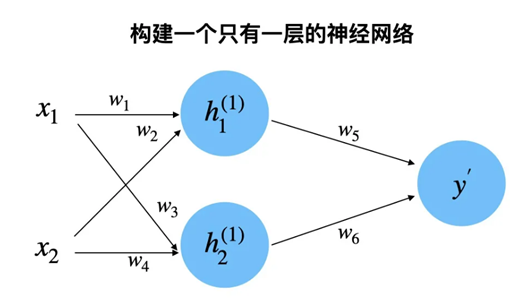
图中参数值如下所示（该例子中省略了激活函数）：

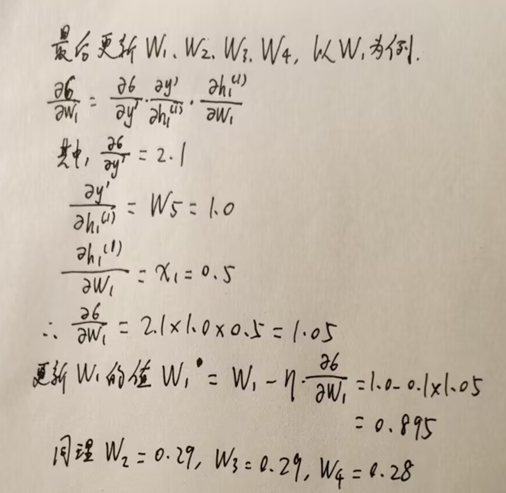
经过第一轮反向传播后参数更新情况如下：

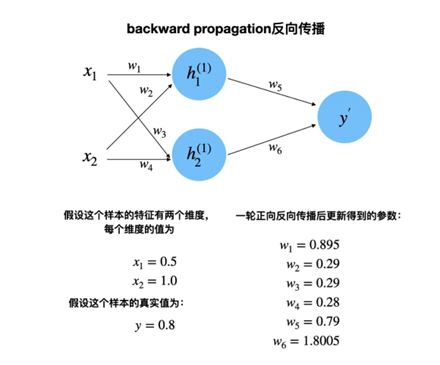
损失函数

概念：
损失函数是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。在应用中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。在统计学和机器学习中被用于模型的参数估计。

适用情形：
从学习任务的类型出发，可以从广义上将损失函数分为两大类——回归损失和分类损失。
（1）在回归任务中，处理的则是连续值的预测问题，例如给定房屋面积、房间数量以及房间大小，预测房屋价格。
（2）在分类任务中，我们要从类别值有限的数据集中预测输出，比如给定一个手写数字图像的大数据集，将其分为 0～9 中的一个。

回归损失函数

均方误差/平方损失/L2 损失：

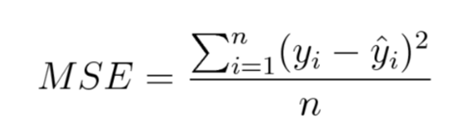
均方误差（mean-square error,MSE）度量的是预测值和实际观测值间差的平方的均值。它只考虑误差的平均大小，不考虑其方向。但由于经过平方，与真实值偏离较多的预测值会比偏离较少的预测值受到更为严重的惩罚。再加上 MSE 的数学特性很好，这使得计算梯度变得更容易。

平均绝对误差/L1 损失：

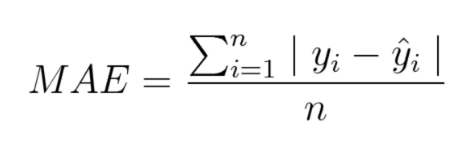
平均绝对误差（Mean Absolute Error，MAE）度量的是预测值和实际观测值之间绝对差之和的平均值。和 MSE 一样，这种度量方法也是在不考虑方向的情况下衡量误差大小。但和 MSE 的不同之处在于，MAE 需要像线性规划这样更复杂的工具来计算梯度。此外，MAE 对异常值更加稳健，因为它不使用平方。

分类损失函数

交叉熵损失/负对数似然（cross-entropy）：
二分类：

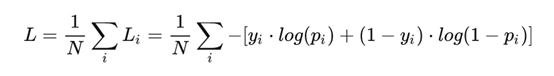
其中：

• yi —— 表示样本 i 的label，正类为 1 ，负类为 0
• pi —— 表示样本 i 预测为正类的概率
  上面的式子是二分类，随着预测概率偏离实际标签，交叉熵损失会逐渐增加。注意，当实际标签为 1(y(i)=1) 时，函数的后半部分消失，而当实际标签是为 0(y(i=0)) 时，函数的前半部分消失。简言之，我们只是把对真实值类别的实际预测概率的对数相乘。还有重要的一点是，交叉熵损失会重重惩罚那些置信度高但是错误的预测值。

多分类：

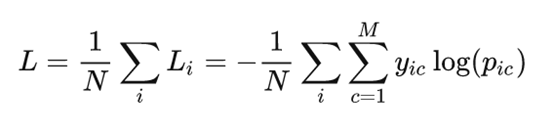
其中：

• M ——类别的数量
• yic ——符号函数（ 0 或 1 ），如果样本 i 的真实类别等于 c 取 1 ，否则取0
• pic ——观测样本 i 属于类别 c 的预测概率
  交叉熵损失函数经常用于分类问题中，特别是在神经网络做分类问题时，也经常使用交叉熵作为损失函数，此外，由于交叉熵涉及到计算每个类别的概率，所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。
  我们用神经网络最后一层输出的情况，来看一眼整个模型预测、获得损失和学习的流程：
  （1）神经网络最后一层得到每个类别的得分scores；
  （2）该得分经过sigmoid(或softmax)函数获得概率输出；
  （3）模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。

总结

在分类问题中，计算交叉熵时只有真实类别的一项会被计算在内，其余项在求和过程均为0。因此即使计算的时候对其他类别的预测概率不准确，只要对真实类别的预测概率较高，损失函数的值仍然较低。