门控循环单元网络(GRU)在自然语言处理中的应用

本文链接：https://blog.youkuaiyun.com/universsky2015/article/details/131907963

本文介绍了门控循环单元网络（GRU）在自然语言处理中的应用，GRU作为一种递归神经网络，解决了传统RNN的梯度消失问题，适用于序列数据建模，尤其在序列分类和标注任务中。文章详细阐述了序列模型的分类、门控机制的概念以及GRU的工作原理，并提供了Python和TensorFlow的实现示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

作者：禅与计算机程序设计艺术

1.简介

自然语言处理（NLP）是人类认知的一项重要技能，它涉及到对文本数据进行处理、提取信息并对其做出回应。传统上，文本分析方法使用基于统计模式的算法，如TF-IDF、朴素贝叶斯等，但这些方法往往忽略了语言结构、上下文、语法和语义，难以处理复杂文本。为了解决这个问题，研究人员提出了基于神经网络的文本分析方法，如卷积神经网络（CNN），递归神经网络（RNN），递归自动编码器（RAE）等。
门控循环单元网络（GRU）是一种递归神经网络，它可以在序列数据中保持记忆，且能够通过控制门来选择需要保留还是丢弃的信息。传统的RNN存在梯度消失或爆炸的问题，而GRU可以有效地解决这一问题。GRU通常比LSTM快很多，而且可以更好地学习长期依赖关系。因此，在自然语言处理中，GRU被广泛应用于序列数据的建模，尤其是在序列分类任务和序列标注任务中。本文将介绍GRU在自然语言处理领域的一些优点以及应用案例。

2.基本概念术语说明

2.1 序列模型

序列模型（Sequence Modeling）是用来处理文本序列的数据建模方法。一般来说，序列模型可以分成三种类型：

1.预测型序列模型（Predictive Sequence Models）

预测型序列模型根据历史记录预测当前词元的概率分布。最常用的预测型序列模型是隐马尔可夫模型（HMM）。HMM认为每个词元是由前面的某些词元决定的，所以每一个词元都有两部分组成：初始状态概率和状态转移概率。用公式表示就是：P(xt|x{1:t−1})=∏pij*P(xj|x{j−1})。其中pj是第i个初始状态概率，xj是第t个词元，xj−1是前一个词元，π是状态转移矩阵，也是隐藏变量。
这种模型很简单，但是它的局限性也很明显。比如：词性标注问题、命名实体识别问题以及文档摘要问题都属于预测型序列模型的范畴。

2.监督型序列模型（Supervised Sequence Models）

监督型序列模型根据训练样本的输出序列预测当前词元的概率分布。最常用的监督型序列模型是条件随机场（CRF）。CRF模型把输入序列看作是一个标记序列，每个词元的标签取自一组可能的标签集合。用公式表示就是：P(y|x)=∏pijpjP(yj|yj+1)。这里的pj和πj是观测变量，yj和yj+1是两个相邻词元之间的标签。CRF模型能够更好地捕获全局结构和局部细节。
比如：机器翻译问题、信息检索问题以及中文分词问题都属于监督型序列模型的范畴。

3.无监督型序列模型（Unsupervised Sequence Models）

无监督型序列模型不依据任何外部信息对输入序列进行建模。它是通过自身的特征表示法（Feature Representation）来学习序列数据中潜藏的结构性信息。最著名的无监督型序列模型是聚类算法（Clustering Algorithms）。聚类算法根据样本之间的距离来确定样本的类别，这种方法能够将相似的样本归为一类。比如：图像聚类、文本聚类以及时间序列聚类都是无监督型序列模型的例子。

2.2 门控机制

门控机制（Gating Mechanism）是指在计算过程中，网络的某些内部结构只能在一定条件下起作用。例如，在循环神经网络（RNN）中，一般情况下网络的内部状态更新的权重是固定的。这种方式导致循环神经网络的梯度流失或爆炸现象。为了解决这个问题，门控机制可以引入一系列门结构，使得网络在一定条件下能够更新状态。门控机制可以分成三种类型：

1.遗忘门（Forget Gate）

遗忘门用于控制网络的忘记能力。当输入的某些信息已经不再重要时，可以通过遗忘门来控制网络的忘记过程，从而减少网络的误差。

2.输入门（Input Gate）

输入门用于控制网络的更新权重。只有当输入足够重要时，网络才会更新状态。

3.输出门（Output Gate）

输出门用于控制网络的输出结果。只有当网络完成一次完整的迭代后，才能输出最终的结果。

2.3 GRU

我们可能会遇到这样的情况：早期观测值对预测所有未来观测值具有非常重要的意义。考虑一个极端情况，其中第一个观测值包含一个校验和，目标是在序列的末尾辨别校验和是否正确。在这种情况下，第一个词元的影响至关重要。我们希望有某些机制能够在一个记忆元里存储重要的早期信息。如果没有这样的机制，我们将不得不给这个观测值指定一个非常大的梯度，因为它会影响所有后续的观测值。

我们可能会遇到这样的情况：一些词元没有相关的观测值。例如，在对网页内容进行情感分析时，可能有一些辅助HTML代码与网页传达的情绪无关。我们希望有一些机制来跳过隐状态表示中的此类词元。

我们可能会遇到这样的情况：序列的各个部分之间存在逻辑中断。例如，书的章节之间可能会有过渡存在，或者证券的熊市和牛市之间可能会有过渡存在。在这种情况下，最好有一种方法来重置我们的内部状态表示。

在学术界已经提出了许多方法来解决这类问题。其中最早的方法是”长短期记忆”（long-short-term memory，LSTM） (Hochreiter and Schmidhuber, 1997)，我们将在 9.2节中讨论。门控循环单元（gated recurrent unit，GRU） (Cho et al., 2014) 是一个稍微简化的变体，通常能够提供同等的效果，并且计算 (Chung et al., 2014)的速度明显更快。由于门控循环单元更简单，我们从它开始解读。

门控循环单元网络（GRU）是一种递归神经网络，它使用了门控机制来控制更新权重，并能够在序列数据中保持记忆。

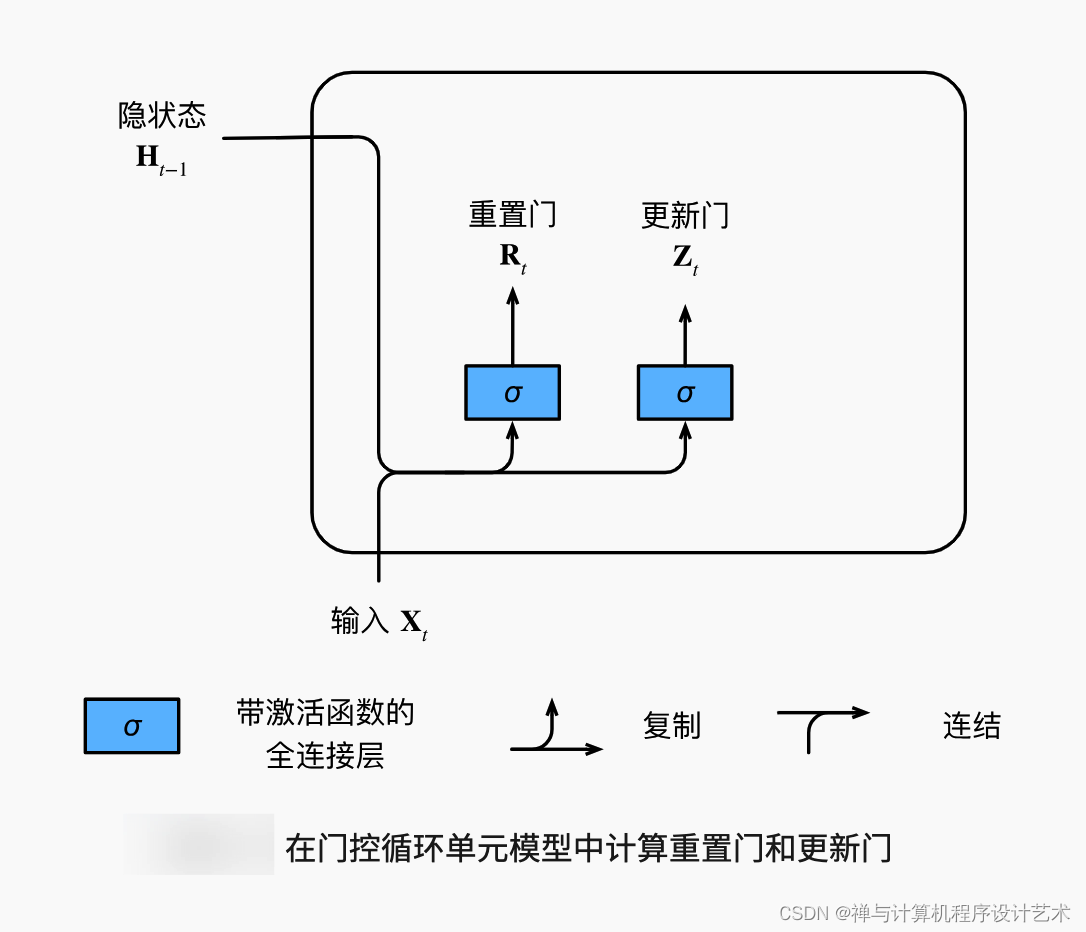
门控循环单元中的重置门和更新门的输入，输入是由当前时间步的输入和前一时间步的隐状态给出。两个门的输出是由使用sigmoid激活函数的两个全连接层给出。

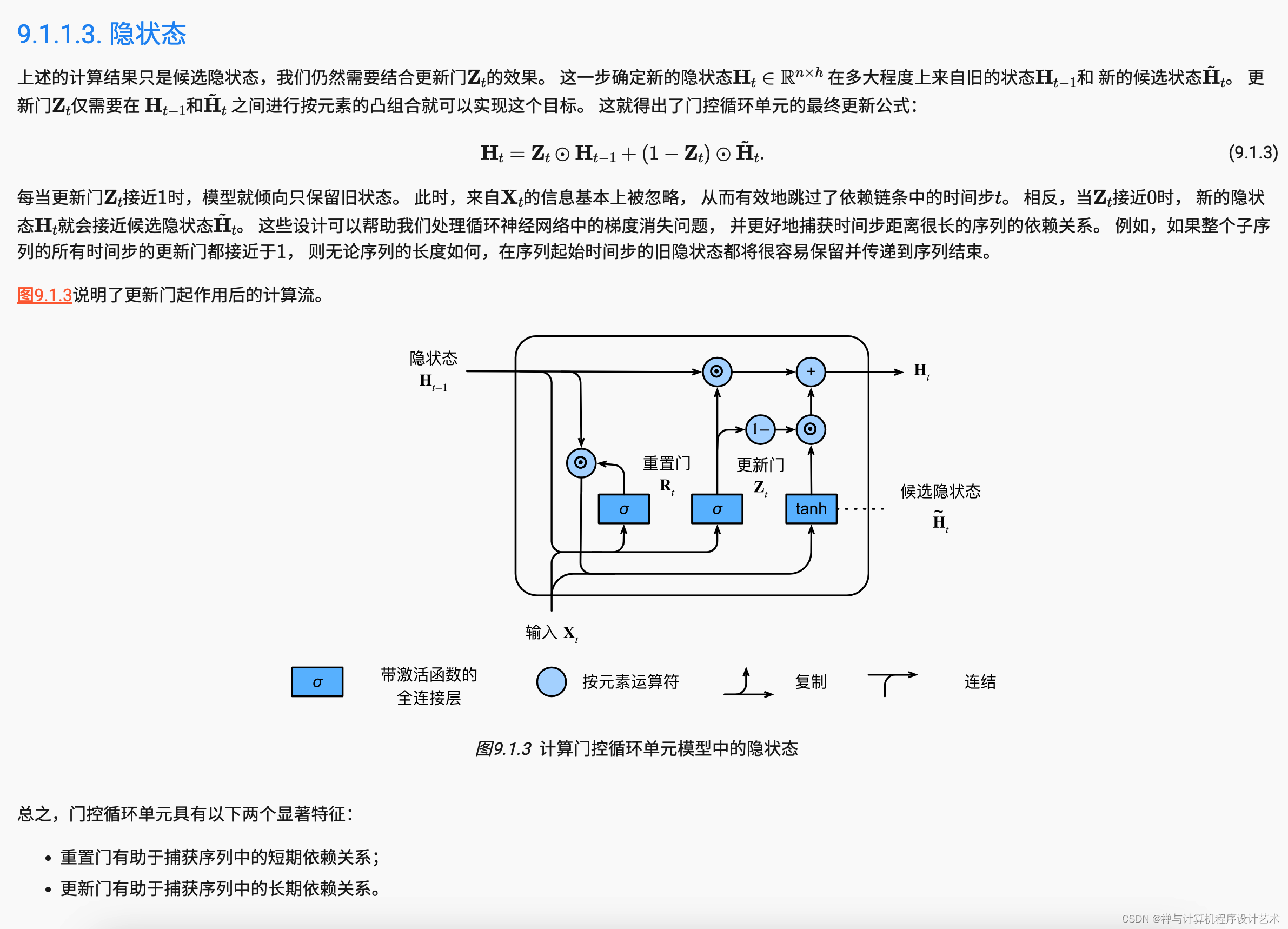
GRU由一个递归单元组成，该单元具有两个门：输入门、遗忘门。输入门用于控制信息进入单元；遗忘门用于控制信息被遗忘。递归单元有三种状态：输入状态、隐含状态、输出状态。输入状态存储着最近的一个时间步的输入，隐含状态则保存了上一次迭代中网络的输出。输出状态则是网络的最后输出。GRU的结构图如下所示。

在这里插入图片描述

https://zh.d2l.ai/chapter_recurrent-modern/gru.html

2.4 提取特征

对于文本序列模型，我们首先要清楚特征是什么，如何抽取？由于文本序列的数据分布不规则，因此，特征的数量也随之增加。常见的特征包括单词级别的特征、字符级别的特征以及位置特征等。下面分别介绍几种常见的特征抽取方法：
1.单词级别的特征：将文本按词进行切分，然后采用统计的方法计算每个词的频率、tf-idf值、左右熵值等作为特征。这样可以帮助网络捕捉到不同词之间的关联性。
2.字符级别的特征：将文本中的每个字符视为一个词，然后采用类似单词级别的特征计算方法。这样的特征能够捕捉到不同字符之间的相互作用。
3.位置特征：除了考虑单词之间、字符之间以及不同词之间的关联性外，还可以考虑不同位置的特征。如当前词前后的固定窗口内的词语、句子等。这对于文本摘要、关键词提取等任务有用处。

3.核心算法原理和具体操作步骤以及数学公式讲解

3.1 激活函数

激活函数（Activation Function）用于对中间层节点的输出进行非线性变换，从而增强模型的非线性表达力。典型的激活函数有Sigmoid、tanh和ReLU。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TqQ5Jlai-1690513283137)(https://aiedugithub4a2.blob.core.windows.net/a2-public/images/65/activation_function.jpg)]

Sigmoid函数：
$\sigma(z) = \frac{1}{1+\exp(-z)}$
sigmoid函数的表达式非常容易理解，计算较为简单，并且在实际计算中经常用作激活函数。
tanh函数：
$\frac{\exp(z)-\exp(-z)}{\exp(z)+\exp(-z)}$
tanh函数也称双曲正切函数，计算结果范围是[-1,1]，因此适合于模型的输出使用。
ReLU函数：
$R e LU (z) = ma x (0, z)$
ReLU函数的作用是让小于0的值变成0，从而增强模型的鲁棒性。

3.2 初始化参数

在训练模型之前，需要对模型的参数进行初始化，否则会出现“矩阵不可逆”、“数值溢出”等问题。在GRU模型中，一般用截断正态分布初始化参数。

3.3 计算过程

GRU模型的计算过程如下图所示：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b6elRTOZ-1690513283138)(https://aiedugithub4a2.blob.core.windows.net/a2-public/images/65/gru_steps.png)]

具体步骤如下：

输入：输入向量 $X=[x_{1}, x_{2},..., x_{T}]$ 。
偏置：将偏置值加入输入信号，获得 $B=\left[b_{f}, b_{r}\right]^{T}$ ，其中 $b_{f}、b_{r}$ 为隐藏层和更新层的偏置值。
更新门： $z^{\left(t\right)}\leftarrow \sigma\left( ilde{h}_{\left(t-1\right)}\right)$ 。$ ilde{h}_{\left(t-1\right)} $是上一步输出的值。其中，$ \sigma$函数为激活函数。
重置门： $r^{\left(t\right)}\leftarrow \sigma\left(W_{ ext {r }} r^{\left(t-1\right)} + U_{ ext {r }} x^{\left(t\right)} + B_{ ext {r }}\right)$ 。 $W_{ ext {r}}$ 、 $U_{ ext {r}}$ 为重置门的权重矩阵； $r^{\left(t-1\right)}$ 为上一步更新门的值； $x^{\left(t\right)}$ 为当前输入的值； $B_{ ext {r}}$ 为重置门的偏置。
候选状态： $KaTeX parse error: Expected 'EOF', got '\right' at position 337: …_{ ext {h }}\̲r̲i̲g̲h̲t̲)$ 。其中， $W_{ ext {h }}、W_{ ext {h }^{*}}、R_{ ext {h }}$ 为候选状态的权重矩阵； $h^{\left(t-1\right)}$ 为上一步的隐含状态； $\bar{z}^{\left(t-1\right)}=z^{\left(t\right)} \circ (1-\bar{z}^{\left(t-1\right)})$ ； $e^{\gamma s r^{\left(t-1\right)}}$ 为序列长度的指数； $u^{\left(t-s\right)}$ 为向前传递的候选状态。
隐含状态： $h^{\left(t\right)}\leftarrow z^{\left(t\right)} \circ h^{\left(t-1\right)} + (1-z^{\left(t\right)}) \circ c^{\left(t\right)}$ 。 $z^{\left(t\right)}$ 为更新门的值， $h^{\left(t-1\right)}$ 为上一步的隐含状态， $c^{\left(t\right)}$ 为候选状态。
输出： $y^{\left(t\right)} \equiv ext{softmax}(V_{o}h^{\left(t\right)}+b_{o})$ 。 $V_{o}$ 为输出层的权重矩阵； $h^{\left(t\right)}$ 为当前隐含状态； $b_{o}$ 为输出层的偏置。
返回输出：返回最后一时间步的输出 $y^{\left(T\right)}$ 。

3.4 训练过程

训练过程是通过反向传播算法来最小化损失函数来优化参数，使得模型更好地拟合数据。常用的优化算法有SGD、Adagrad、Adam等。GRU模型的训练过程比较直观，不需要进行特别的设计。

4.具体代码实例和解释说明

4.1 Python实现

以下是Python代码实现GRU模型：

import numpy as np


class GruNet:
    def __init__(self, input_size, hidden_size):
        self.input_size = input_size    # 输入维度
        self.hidden_size = hidden_size  # 隐藏层维度

        # 定义参数
        self.Wf = np.random.randn(input_size + hidden_size, hidden_size) / np.sqrt(hidden_size)   # 输入-隐层权重
        self.Wi = np.random.randn(input_size + hidden_size, hidden_size) / np.sqrt(hidden_size)   # 输入-隐层权重
        self.Wo = np.random.randn(input_size + hidden_size, hidden_size) / np.sqrt(hidden_size)   # 输入-隐层权重
        self.Wc = np.random.randn(input_size + hidden_size, hidden_size) / np.sqrt(hidden_size)   # 输入-隐层权重
        self.Rb = np.zeros((1, hidden_size))                                                     # 偏置
        self.Ri = np.zeros((1, hidden_size))                                                     # 偏置
        self.Ro = np.zeros((1, hidden_size))                                                     # 偏置
        self.Rc = np.zeros((1, hidden_size))                                                     # 偏置

    def forward(self, X, h_prev):
        """前向传播"""
        T = len(X)
        H = np.zeros((T, self.hidden_size))
        for t in range(T):
            # 当前输入
            xt = X[t].reshape(1, -1)

            # 输入门
            zt = sigmoid(np.dot(np.concatenate([xt, h_prev], axis=1), self.Wf) +
                         np.dot(np.concatenate([xt, h_prev], axis=1), self.Wi) +
                         self.Rb * np.ones((1, 1)))

            # 重置门
            rt = sigmoid(np.dot(np.concatenate([xt, h_prev], axis=1), self.Wr) +
                         np.dot(np.concatenate([xt, h_prev], axis=1), self.Ui) +
                         self.Rr * np.ones((1, 1)))

            # 候选状态
            ct = np.tanh(np.dot(np.concatenate([xt, rt * h_prev], axis=1), self.Wc) +
                          self.Rc * np.ones((1, 1)))

            # 隐含状态
            ht = (1 - zt) * h_prev + zt * ct
            H[t] = ht

            # 下一时刻的隐含状态
            h_prev = ht

        return H

    def backward(self, X, Y, h_prev):
        """反向传播"""
        T = len(X)
        dWf = np.zeros((self.input_size + self.hidden_size, self.hidden_size))
        dWi = np.zeros((self.input_size + self.hidden_size, self.hidden_size))
        dWo = np.zeros((self.input_size + self.hidden_size, self.hidden_size))
        dWc = np.zeros((self.input_size + self.hidden_size, self.hidden_size))
        dRb = np.zeros((1, self.hidden_size))
        dRi = np.zeros((1, self.hidden_size))
        dRo = np.zeros((1, self.hidden_size))
        dRc = np.zeros((1, self.hidden_size))

        dh_next = np.zeros((1, self.hidden_size))
        for t in reversed(range(T)):
            # 当前输入
            xt = X[t].reshape(1, -1)

            # 前一时刻的隐含状态
            if t == T - 1:
                h_prev = np.zeros((1, self.hidden_size))
            else:
                h_prev = H[t+1][0]

            # 输出层
            yt_pred = softmax(np.dot(h_prev, self.Vo) + self.bo)

            # 误差
            dt = (yt_pred - Y[t])
            db = dt
            dV = np.dot(dt, h_prev.transpose())

            # 当前时间步的损失
            dy = np.dot(dV, self.Vo.transpose())

            # 计算梯度
            dz = dy * h_prev + (1 - h_prev) * dy
            dr = self.Wc.T @ (dh_next + (1 - h_prev) * dh_next) + dt * (
                    self.Wc[:, :self.hidden_size].T @ h_prev) + self.Rb * dt
            dc = self.Wc.T @ ((1 - h_prev) * dh_next) + dt * (
                    self.Wc[:, :self.hidden_size].T @ (1 - h_prev)) + self.Rb * dt
            dx = dy * self.Wo[:self.input_size] + dt * (self.Wo[:self.input_size, :self.hidden_size].T @
                                                    (h_prev + (1 - h_prev) * h_prev))
            dwf = np.dot(np.concatenate([xt, h_prev], axis=1).transpose(), dz * rt * (1 - ct ** 2))
            dwi = np.dot(np.concatenate([xt, h_prev], axis=1).transpose(), dz * rt * (1 - ct ** 2))
            dwo = np.dot(np.concatenate([xt, h_prev], axis=1).transpose(), dz * (1 - h_prev) * (1 - ct ** 2))
            dwc = np.dot(np.concatenate([xt, h_prev], axis=1).transpose(), dz * (1 - h_prev) * (1 - ct ** 2))
            drb = dz * rt * (1 - ct ** 2)
            dirn = np.dot(np.concatenate([xt, h_prev], axis=1).transpose(), dz * (1 - h_prev) * (1 - ct ** 2))
            dro = dz * (1 - h_prev) * (1 - ct ** 2)
            drc = dz * (1 - h_prev) * (1 - ct ** 2)
            dh_prev = np.dot(dz, self.Wf.T) + np.dot(dr, self.Wr.T) + np.dot(dc, self.Wc.T) + np.dot(dx, self.Wm.T)

            # 累加梯度
            dWf += dwf
            dWi += dwi
            dWo += dwo
            dWc += dwc
            dRb += drb
            dRi += dirn
            dRo += dro
            dRc += drc

        return [dWf, dWi, dWo, dWc, dRb, dRi, dRo, dRc]

以上是GRU模型的Python代码实现。

4.2 TensorFlow实现

以下是TensorFlow代码实现GRU模型：

import tensorflow as tf

class GruNet(object):
    def __init__(self, vocab_size, embedding_dim, hidden_dim, batch_size):
        self.vocab_size = vocab_size      # 词汇表大小
        self.embedding_dim = embedding_dim  # 词向量维度
        self.hidden_dim = hidden_dim        # 隐藏层维度
        self.batch_size = batch_size        # mini-batch大小

        with tf.name_scope('inputs'):
            self.xs = tf.placeholder(shape=(None, None), dtype=tf.int32, name='xs')   # 输入序列
            self.ys = tf.placeholder(shape=(None, None), dtype=tf.int32, name='ys')   # 标签序列
            self.dropout_keep_prob = tf.placeholder(dtype=tf.float32, name='dropout_keep_prob')  # dropout的保留率

        with tf.variable_scope('embedding'):
            embeddings = tf.Variable(tf.random_uniform([self.vocab_size, self.embedding_dim], -1.0, 1.0),
                                      trainable=True, name='embeddings')  # 词嵌入矩阵
            embedded = tf.nn.embedding_lookup(params=embeddings, ids=self.xs)  # 根据输入序列得到词向量

        with tf.name_scope('gru'):
            gru_cell = tf.contrib.rnn.GRUCell(num_units=self.hidden_dim)
            initial_state = gru_cell.zero_state(self.batch_size, tf.float32)
            output, _ = tf.nn.dynamic_rnn(cell=gru_cell, inputs=embedded,
                                            initial_state=initial_state, time_major=False,
                                            dtype=tf.float32)

        with tf.name_scope('output'):
            w = tf.Variable(tf.truncated_normal([self.hidden_dim, self.vocab_size]),
                            name='w')     # 输出层权重矩阵
            b = tf.Variable(tf.constant(0.1, shape=[self.vocab_size]), name='b')   # 输出层偏置向量
            logits = tf.matmul(output, w) + b           # 输出层预测值
            predictions = tf.argmax(logits, axis=2, name='predictions')   # 对数似然

        with tf.name_scope('loss'):
            losses = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=tf.reshape(self.ys, [-1]),
                                                                       logits=tf.reshape(logits, [-1, self.vocab_size]))
            loss = tf.reduce_mean(losses)                     # 交叉熵损失

        with tf.name_scope('optimizer'):
            optimizer = tf.train.AdamOptimizer()             # Adam优化器
            gradients, variables = zip(*optimizer.compute_gradients(loss))  # 计算梯度
            clipped_gradients, global_norm = tf.clip_by_global_norm(gradients, clip_norm=5)  # 裁剪梯度
            train_op = optimizer.apply_gradients(zip(clipped_gradients, variables))   # 更新参数

        with tf.name_scope('accuracy'):
            correct_predictions = tf.equal(tf.cast(tf.reshape(predictions, [-1]), tf.int32),
                                           tf.cast(tf.reshape(self.ys, [-1]), tf.int32))   # 判断预测结果是否正确
            accuracy = tf.reduce_mean(tf.cast(correct_predictions, tf.float32), name='accuracy')   # 准确率

        self.inputs = {'Xs': self.xs, 'Ys': self.ys, 'DropoutKeepProb': self.dropout_keep_prob}
        self.outputs = {'Predictions': predictions, 'Accuracy': accuracy, 'Loss': loss,
                        'TrainOp': train_op}