【leetcode刷题日记】lc.240-搜索二维矩阵 II

目录

1.题目

2.代码

---

1.题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

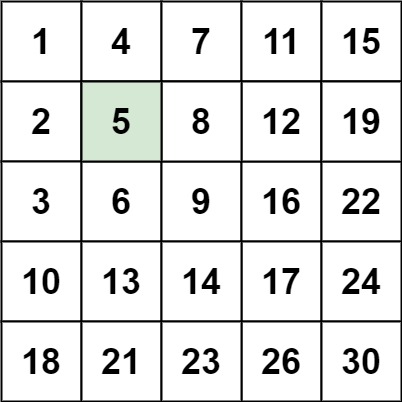
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

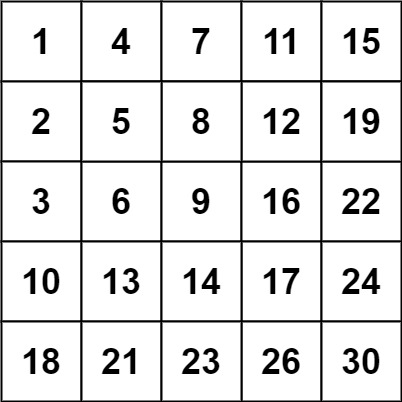
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matrix[i][j] <= 109
• 每行的所有元素从左到右升序排列
• 每列的所有元素从上到下升序排列
• -109 <= target <= 109

2.代码

class Solution {
public:
    int binary(vector<int> &tmp,int tar)
    {
        int l = 0;
        int r = tmp.size();
        int mid = 0;
        while(l<r)
        {
            mid = (l+r)/2;
            if(tmp[mid]<tar)
            {
                l=mid+1;
            }
            else if(tmp[mid]>tar)
            {
                r=mid;
            }
            else
            {
                return mid;
            }
        }
        return -1;
    }

    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n = matrix.size();
        int m = matrix[0].size();
        for(int i=0;i<n;i++)
        {
            int k = binary(matrix[i],target);
            if(k!=-1)
            {
                return true;
            }
        }
        return false;
    }
};