【数据结构】从BFS到迪杰斯特拉

最新推荐文章于 2024-10-24 23:36:17 发布

原创

最新推荐文章于 2024-10-24 23:36:17 发布 · 574 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #图论 #dijkstra

本文从BFS遍历的角度出发，探讨如何利用广度优先搜索思想解决有权图的最短路径问题。通过引入优先队列，详细阐述了迪杰斯特拉算法的原理和实现，适用于无负权图，无论是有向还是无向，有环或无环。

从BFS到迪杰斯特拉

回顾图的BFS遍历

我们知道，图的BFS遍历有一个“附加功能”，就是可以求得无权图两点间的最短距离。
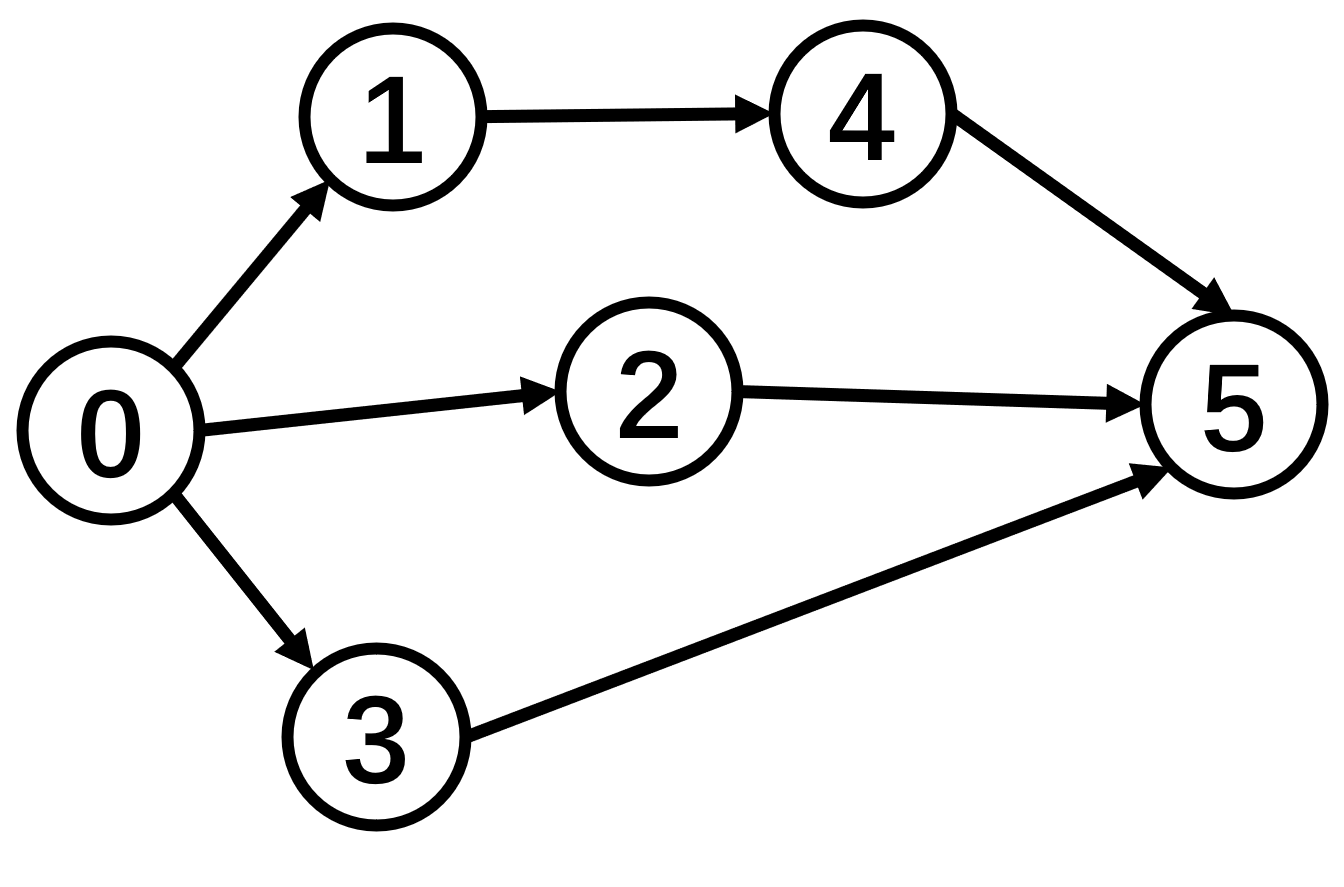
一个无权有向图
对图进行BFS遍历的过程很简单：
借助一个队列，首先起始节点入队，当队列不空的时候，弹出队首元素，再将其后继节点入队，不断重复这个过程。

下面，以0为起始点对上图进行广度优先遍历：

操作	队列
第一步：0入队	0
第二步：访问0，1、2、3入队	1 2 3
第三步：访问1，4入队	2 3 4
第四步：访问2，5入队	3 4 5
第五步：访问3	4 5
第六步：访问4	5
第七步：访问5	null

分析广度优先遍历能够找到无权图最短路的原因

一个假设：假设无权图也是有权图，权值相等且均为1
那么，我们可以把刚才那个有向无权图转化成如下有向有权图：
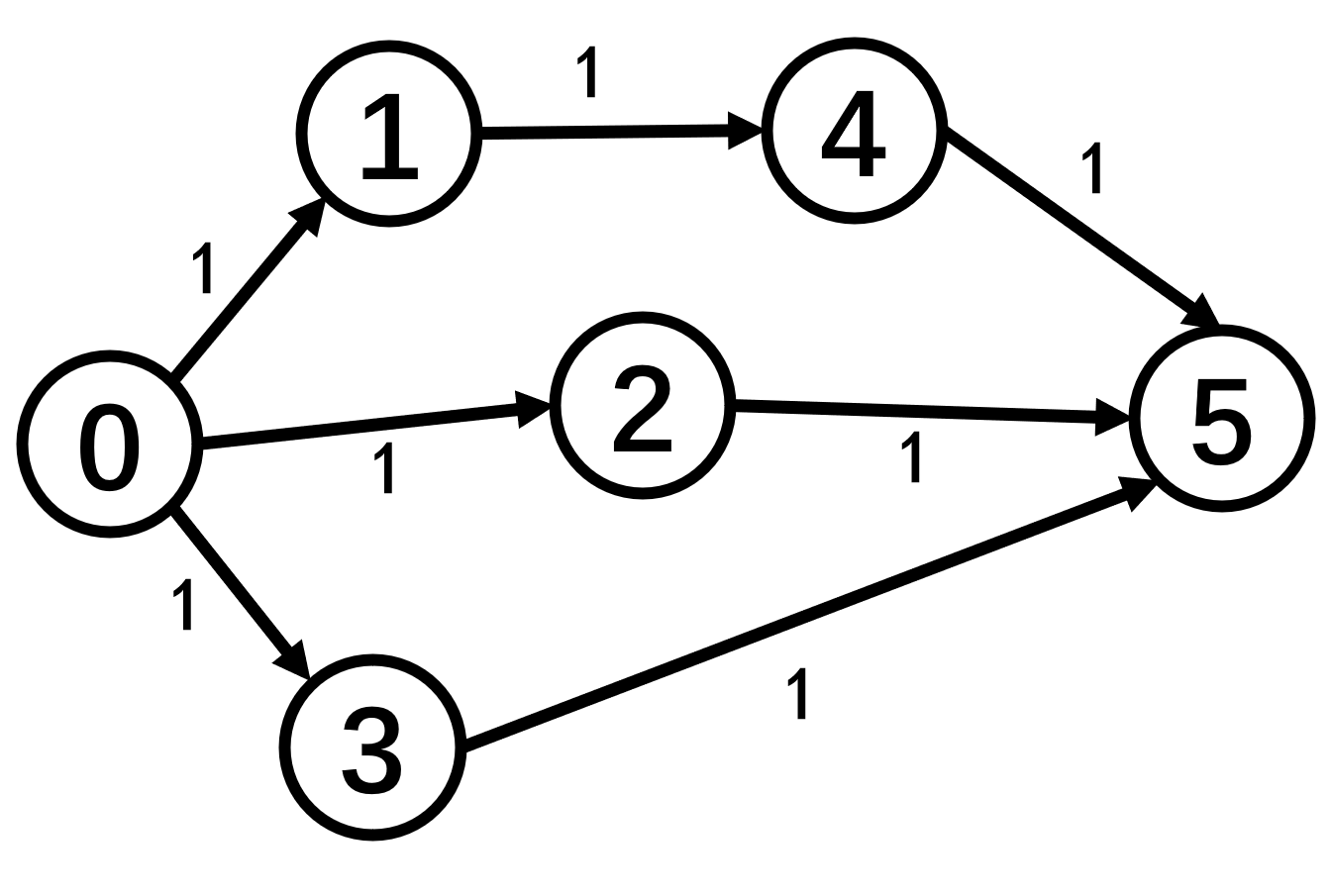
规定无权图权值均为1
我们来观察一下广度优先遍历时队列中的元素
0 1 2 3 4 5
他们距离起始点0的距离是：0 1 1 1 2 3
可以发现，这是一个递增的序列，先入队的距离起始点更近，后入的距离起始点更远。

由广度优先遍历转向迪杰斯特拉算法

显然，刚才发现的规律是由于无权图“众边平等”的特点造成的；更加显然的是，有权图不具备这个特点。
如下有权图中，距0的距离为：0 1 5 4 3 6

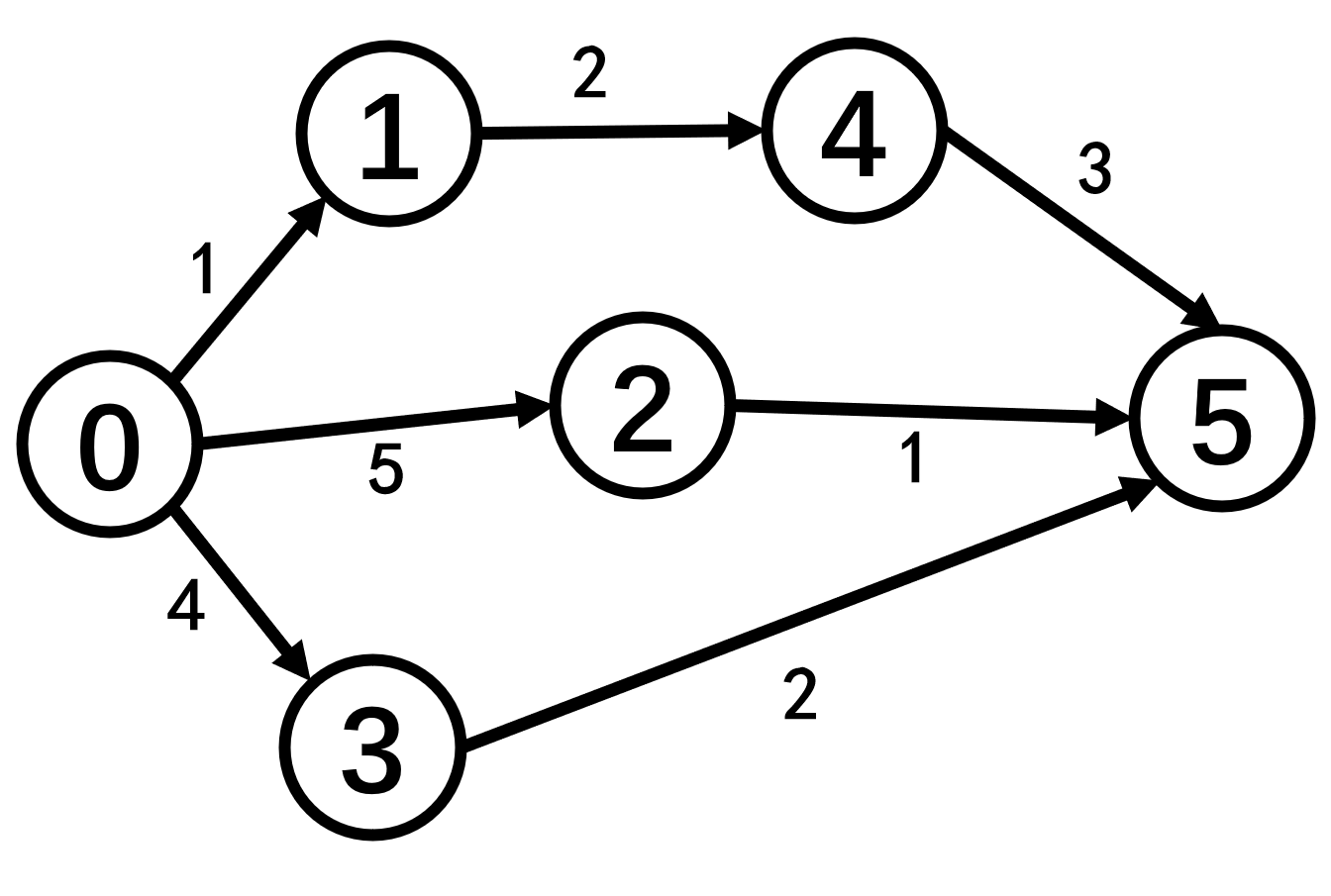
那么，能不能通过某种方式，借助广度优先遍历的思想去寻找有权图的最短路呢？（没有我就不问了（ε=ε=ε=┏(゜ロ゜;)┛））

想象一下，如果有一个附带排序功能的队列，每次节点入队时，都将最小的节点置于队首，那这样不就模拟出广度优先遍历时，“距离短的先入队，距离长的后入队”的规律了吗？

这种队列被称作优先队列

下面给出优先队列类的实现：
（C++ STL和其他语言的库里有封装好的优先队列，可以自己写一写STL里面的东西，挺有意思的）

template<class T>class PriorityQueue//优先队列
{
   
   
private:
    int size = 1;//队列的容量，初始值为1
    int length = 0;//队列已经占用的长度
    int head = 0;//队首下标
    int tail = 0;//队尾下标
    T** queue = new T * [size];
public:
    PriorityQueue()//构造方法
    {
   
   
        memset(queue, 0, size * sizeof(T*));
    }
    bool empty()//队列是否为空
    {
   
   
        return head == tail;
    }
    void push(const T& a)//入队
    {
   
   
        for (int i = head; i <= tail; i++)//将元素插入对应位置
        {
   
   
            if (i == tail ||*queue[i] < a) {
   
   
                for (int j = tail; j >= i; j--) {
   
   
                    queue[j] = queue[j - 1];
                }
                queue[i] = new T(a);
                tail++;
                length++;
                break;
            }
        }
        if (length == size) //如果队列大小不够就自动扩容，每次扩容大小为原来的二倍
        {
   
   
            T** temp = queue;
            size <<= 1;
            queue = new T * [size];
            memmove(queue, temp + head, (tail - head) * sizeof(T*));
            delete[] temp;
            length = tail - head;
            tail -=</