#include <algorithm>
参考资料:
比较树:
知识点参考文档
1.树节点 键值(key)的比较
2.叶子/尾结点/外节点
其他节点/内节点
3.一个特定查找算法中做的比较次数,就是从树的顶(我们叫它“根”)到某个适当“叶”之间路径上所有遍历的内节点数量。
binary_search_1
1.binary_search_1的比较统计:每次查找都在叶节点处结束。
2.为了获取成功查找及失败查找的比较平均数,我们需要使用树的“外径长”:它是遍历每个叶节点到根节点时,所经过的树枝的数量总和。
3.其中一半的叶节点符合成功查找,另一半是失败查找。
因此n=10时,binary_search_1的成功查找或非成功查找的比较平均数,都是4.4。
binary_search_2
1.三路比较,把两种比较合并成一种。
2.意味着每个叶节点都是以非成功查找结束的,每个非叶节点都是符合成功查找。
3.每个所示的节点都进行了两次比较,除非在某个节点上成功找到目标键的话,那么它就只进行了一次比较。
4.binary_search_2的比较统计:(除非在节点上找到目标键)每个非叶节点都进行了两次比较。被遍历的内部节点数,要比经过的树枝数多1(对于每个n=10时的内节点)。因此我们获取成功查找的比较平均数是4.8。
公式中的(-1),是因为实际中,当目标键被找到时,少做了一次比较。
-
失败查找:因此树的外径长指的只是失败查找的比较次数。
-
成功查找:“内径长”,它被定义为,所有非叶节点到根节点遍历所经过的树枝总数。
-
内径计算如下图:
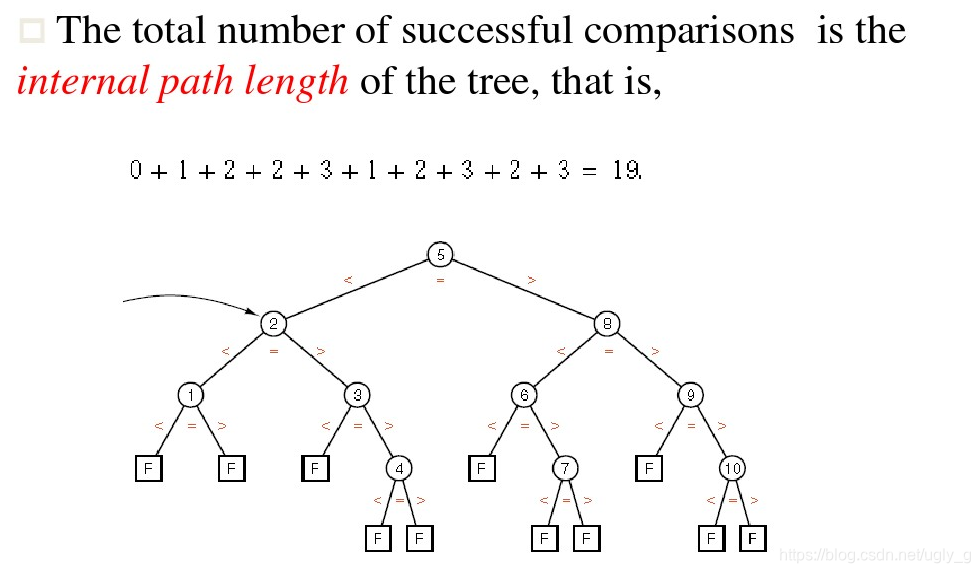

关于算法的比较

比较树和递归树,对于递归算法来说,这两种事情经常被视为同种事情。
从n=10时的binary_search_1和binary_search_2的树图来看,很容易能看出每个算法要进行多少次比较。最坏的查找情况,就是这个数字比树的高还要多1。
实际上对于每次查找来说,它都是在查从根节点到叶节点之间的节点数。
- binary_search_1的分析


- binary_search_2分析(成功查找)


路长定理
目的:为了计算binary_search_2中成功查找的键比较平均数。
定理:用E表示二树的外径长,用I表示内径长,q表示非叶节点的总数,那么E=I+2q



查找的下限

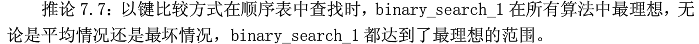
其他查找问题

比较树部分定义

关于外径和内径的概念

sequential顺序查找
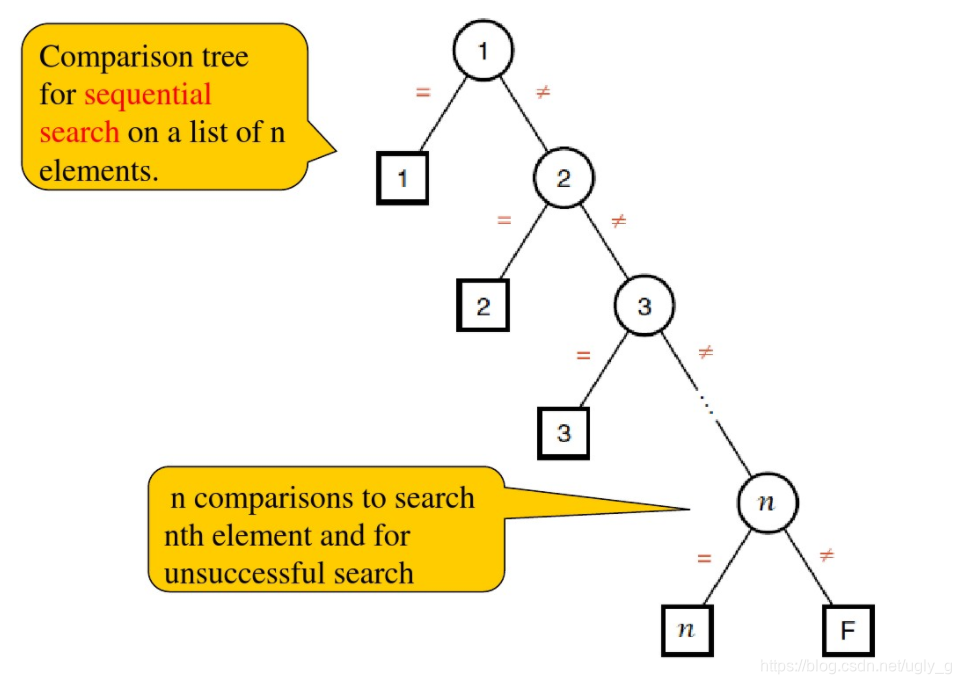
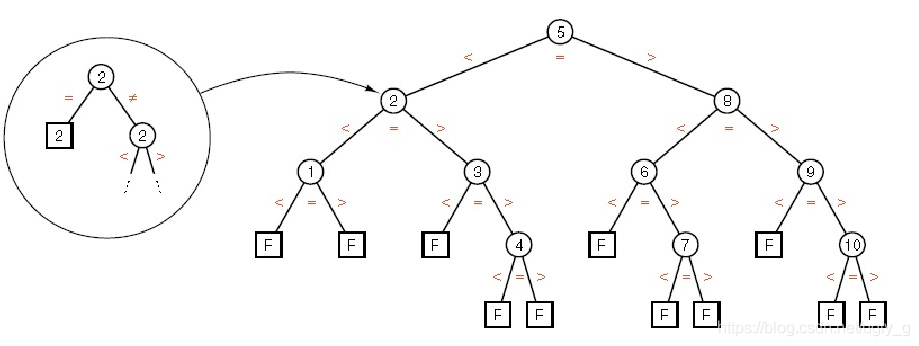
比较平均次数计算
(算出平均经过的树枝数后加一表示结点数,当没有找到Key时,在每个结点比较两次)

关于二树

在BB上的例题:
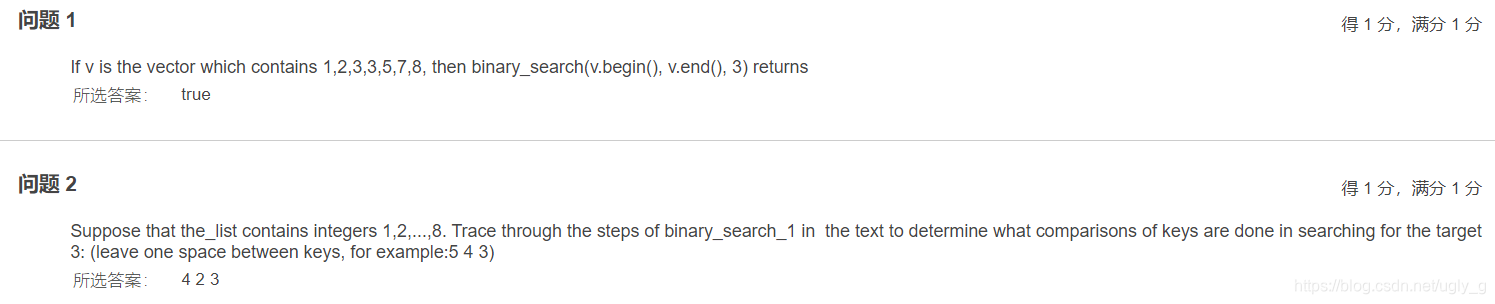
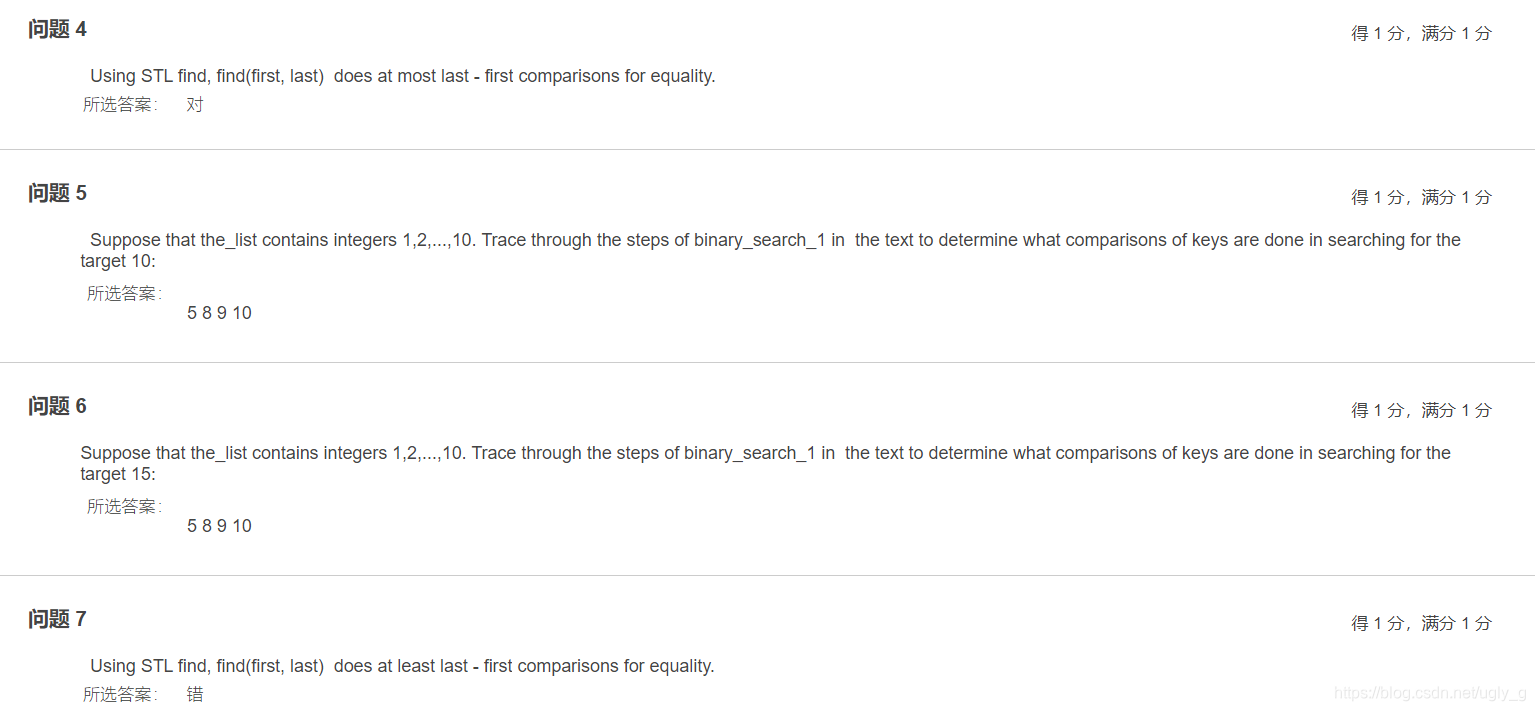
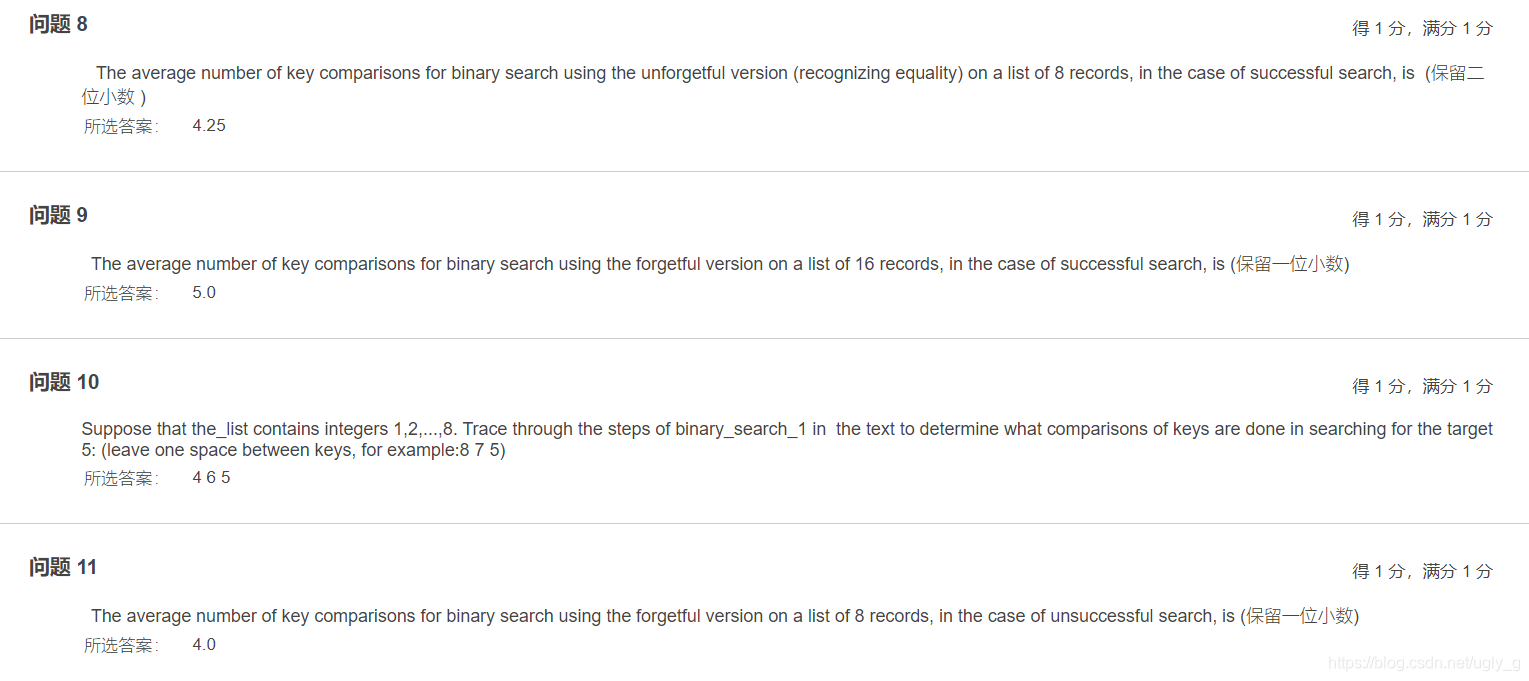






 本文深入探讨了二分查找算法与比较树的概念,详细分析了binary_search_1和binary_search_2两种二分查找变体的比较次数统计,阐述了成功查找与失败查找的平均比较次数计算方法,以及路长定理的应用。通过对比两种算法,揭示了不同查找策略下的性能差异。
本文深入探讨了二分查找算法与比较树的概念,详细分析了binary_search_1和binary_search_2两种二分查找变体的比较次数统计,阐述了成功查找与失败查找的平均比较次数计算方法,以及路长定理的应用。通过对比两种算法,揭示了不同查找策略下的性能差异。
















 1246
1246

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








