引入回归算法
什么是“回归”？
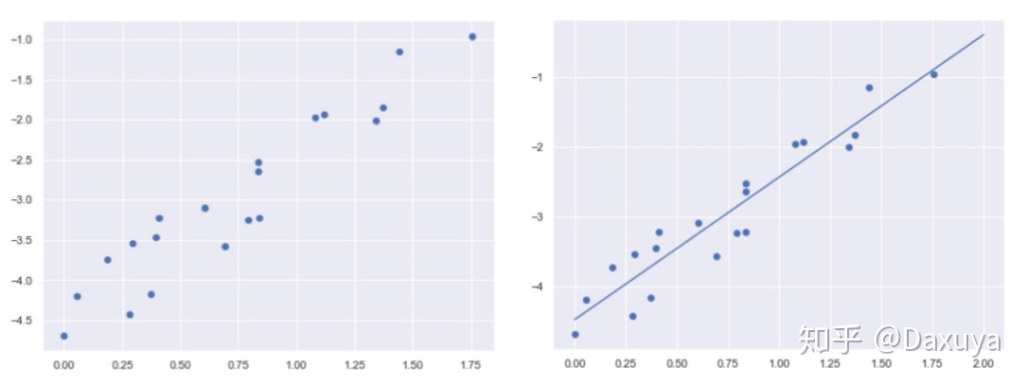
回归的全称是，“Regression towards the mean”。**直接翻译过来就是向着中间值回归。直白点说，就是在图像上给你一堆点，你来找一条线，然后让这条线尽可能的在所有点的中间。**这个找直线的过程，就是在做回归了。如下图所示
进一步思考：为什么非要找这么一条尽可能的在所有点的中间的直线？
我们面对的是一堆散乱的点，看不出具体的相关关系，而线能够体现趋势。所以，我们就是想办法来找一条尽可能在所有点的中间的直线，代表一个数据的整体趋势，让数据的整体关系更加清晰可见，这样就方便我们预判未来的情况
总结:
回归的目的：通过找到的线来预测未来
回归之所以能预测，是因为它的底层逻辑是：通过历史数据，摸透了“套路”，然后通过这个套路来预测未来的结果
什么是“线性”？
“线性”就是说，“回归”找到的线是直的。
线性关系不仅仅只能存在 2 个变量（二维平面）。3 个变量时（三维空间），线性关系就是一个平面，4 个变量时（四维空间），线性关系就是一个体。以此类推…
什么是线性回归？
如果你在上面找线的过程所找的线直的（即是线性的），那么这个找直线的过程就是“线性回归”
线性回归(LR)可分为：简单一元线性回归和多元线性回归，也就是我们平时接触的一次线性方程和多次线性方程，二者的主要区别也就是未知项的个数
什么是回归算法
- 回归算法是一种有监督算法
- 建立“解释”变量(自变量X)和观测值(因变量Y)之间的关系
- 从机器学习的角度来讲，用于构建一个算法模型(函数)来做属性(X)与标签(Y)之间的映射关系，在算法的学习过程中，
试图寻找一个函数 h : R d − > R h: R^d->R h:Rd−>R，使得参数之间的关系拟合性最好。
- 回归算法中算法(函数)的最终结果是一个连续的数据值，输入值(属性值)是一个d维度的属性/数值向量
线性回归
作用: 连续值的预测
最优模型: 最优模型也就是所有样本(训练数据)离模型的直线或者平面距离最小
线性关系: 特征属性X和目标属性Y之间的关系是满足线性关系
KaTeX parse error: {split} can be used only in display mode.
- 目标属性h(x)，x代表特征值，x前面的代表参数，θ要求解的。求出后就可以确定h(x)
- θ(T): (1, n), x: (n, 1), 等号右边是一个标量
- 机器学习中通常采用列向量为基本向量，所以需要要把θ转置为行向量
损失函数
如何找到“合适”的那条直线？
两步解决：
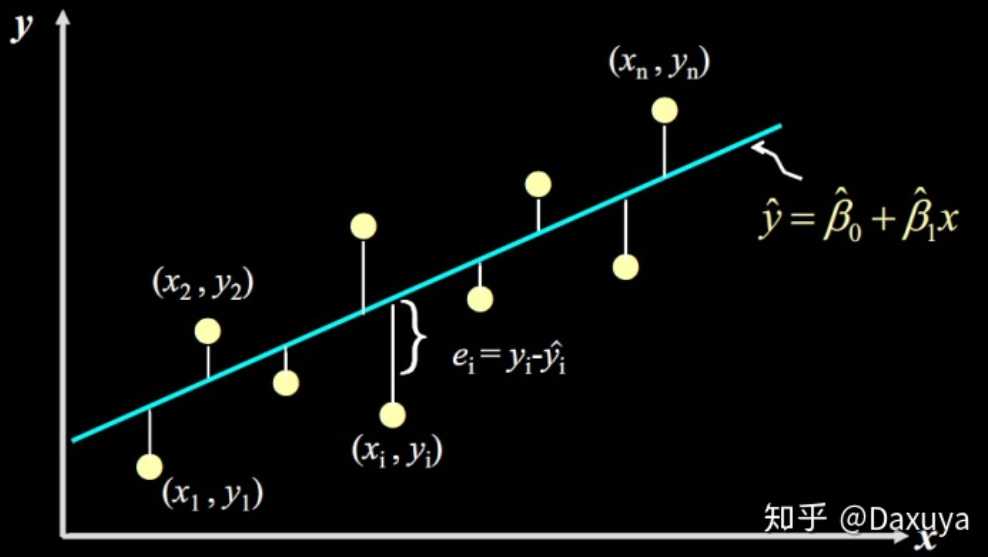
step1：想办法表示出这条直线到所有数据点的距离
step2：让这个距离最小！
- 假设函数计算出的点 y i ^ \hat{y_i} yi^** 与真实数据点** y \text{y} y的间隔（差值）就是我们要找的点到直线的距离。机器学习里将这个差值叫误差，其表达式：
ε = y i − y ^ i \varepsilon=y_i-\hat{y}_i ε=yi−y^i
∑ ε 2 = ∑ ( y − y ^ i ) 2 = ∑ ( y − w 0 − w 1 x ) 2 \sum\varepsilon^2=\sum(y-\hat y_i)^2=\sum(y-w_0-w_1x)^2 ∑ε2=∑(y−y^i)2=∑(y−w0−w1x)2
- 在机器学习中，人们也称误差为损失，所以这种求误差的方法也可以说是求损失的方法。而SSE也就是线性回归中最常用的损失函数了
最小二乘法
计算预测值和实际值的差值的平方然后求出这个值的最小值对应的参数, 就是我们要的模型
经验误差：回归模型在训练集上的误差
泛化误差：回归模型在测试集上的误差
KaTeX parse error: {align} can be used only in display mode.
- 差值有正有反，会互相抵消，用平方来避免。ε代表差值。其中1/2是为了后面方便求导，不会对所求产生影响
- 求出这个差值函数的最小值时的参数值得到模型
- 房价预测
最大似然估计
最大似然估计(maximum likelihood estimation，MLE)：估计参数的方式，投掷硬币，独立事件，同时发生的概率， 即每个事件发生概率相乘，就是联合概率，联合概率越大越好，关于参数p的似然函数，极大化，取对数，求最大值
正态分布
- 理想误差 ε ( i ) ( 1 ≤ i ≤ n ) \varepsilon^{(\mathrm{i})}(1 \leq i \leq n) ε(i)(1≤i≤n)，独立同分布的，服从均值为0，方差为某 θ 2 \theta^2 θ2定值的高斯分布(就是正态分布)
- 随机现象可以看做众多因素的独立影响的综合反应，往往服从正态分布，。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。误差出现的概率：
KaTeX parse error: {align} can be used only in display mode.
- **原因：**中心极限定理，解释了为什么服从正态分布
似然函数
KaTeX parse error: {align} can be used only in display mode.
KaTeX parse error: {align} can be used only in display mode.
KaTeX parse error: {align} can be used only in display mode.
此式表示，在 θ \theta θ和 x （ i ） x^{（i）} x（i）下， y （ i ） y^{（i）} y（i）符合程度，即概率
KaTeX parse error: {align} can be used only in display mode.\thetaKaTeX parse error: Expected 'EOF', got '}' at position 17: …的似然估计-联合概率-似然函数}̲\\ \end{align}
ln L ( θ ) \ln L(\theta) lnL(θ)要极大化似然函数，值越大说明越符合模型，即可得到最大化下的 θ \theta θ
似然函数取对数
目的: ln L ( θ ) \ln L(\theta) lnL(θ)需要处理才可方便计算，一般都是取对数，结果如下：
KaTeX parse error: {align} can be used only in display mode.
得到结果和最小二乘法一样!!!
据此,我们求合适的直线问题就转化为了，极大化似然函数转化求 J ( θ ) J(\theta) J(θ)的最小值，即求出 θ \theta θ的最优解
目标函数的求解过程
KaTeX parse error: {align} can be used only in display mode.
KaTeX parse error: {align} can be used only in display mode.
对 J ( θ ) J(\theta) J(θ)求偏导，就是求梯度 ∇ θ \nabla_\theta ∇θ，梯度意味着是对 θ \theta θ内每一个参数求导了，求导公式如下：
∂ A ⋅ x ∂ x = A T ∂ x ⋅ A ∂ x = A ∂ A ⋅ x ∂ x T = A ∂ x ⋅ A ∂ x T = A T ∂ x T x ∂ x = 2 x ∂ x T A x ∂ x = ( A + A T ) x \begin{array}{c} \frac{\partial A \cdot x}{\partial x}=A^T \quad \frac{\partial x \cdot A}{\partial x}=A \\ \frac{\partial A \cdot x}{\partial x^T}=A \quad \frac{\partial x \cdot A}{\partial x^T}=A^T \\ \frac{\partial \mathbf{x}^{\mathbf{T}} \mathbf{x}}{\partial \mathbf{x}}=2 \mathbf{x} \\ \frac{\partial \mathbf{x}^{\mathbf{T}} \mathbf{A} \mathbf{x}}{\partial \mathbf{x}}=\left(\mathbf{A}+\mathbf{A}^{\mathbf{T}}\right) \mathbf{x} \end{array} ∂x∂A⋅x=A
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
