GBoost 和 xGBoost

原创已于 2022-05-24 17:44:25 修改 · 1.8k 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #决策树 #算法

于 2019-02-22 11:07:19 首次发布

综合-机器学习理论专栏收录该内容

77 篇文章

订阅专栏

本文深入解析GB、GBDT与xgboost三种提升算法，详细阐述了GBoost算法的基础，包括其与AdaBoost的区别，以及如何通过一阶导数训练弱分类器。此外，还介绍了xGBoost的泰勒展开思想，以及如何通过损失函数确定Tree结构，最后对比了GB、GBDT与xgboost的不同。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

背景知识：AdaBoost / BoostTree

一、GBoost

对于GBoost的讲解将在BoostTree的基础上进行，如果大家对BoostTree不了解，可以参考上述列出的博文。
BoostTree本质：

将AdaBoost的弱分类器定为了“决策树”；
采用第m-1次训练得到的分类器fm-1(xi)的值与label yi的残差，来训练第m次的弱分类器Gm(x)，这里fm(x) = fm-1(x) + Gm(x)；

与BoostTree相比，GBoost不是使用残差来训练弱分类器，而是使用损失函数一阶导来作为残差的近似值，训练弱分类器。即：利用一阶导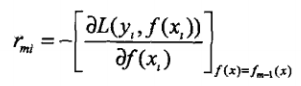作为训练第m次弱分类器的sample。对于平方损失 L=(yi - fm-1(xi))²来讲，其关于fm-1(xi)的导数为：2(yi - fm-1(xi))，与残差公式相近，而对于logistic损失来讲，则可用损失函数L的一阶导来近似残差： yi - fm-1(xi)。

GBoost算法伪代码如下：

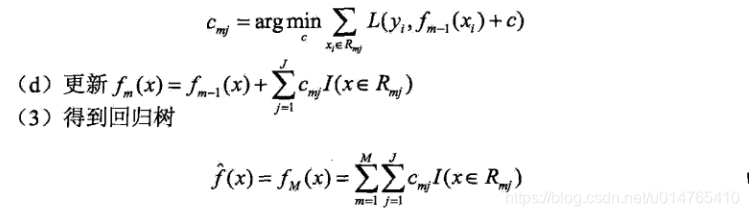
在实际应用中，我们可以对GBoost分类器添加一个shrinkage（0.1），即：fm(x) = fm-1(x) + shrinkage * Gm(x)，shrinkage的作用是使每次拟合的弱分类器只能拟合残差的部分值，从而使得残差的拟合从“一步到位” 变为了 “分很多小步逐渐实现完全拟合”，这种做法可以有效防止GBoost过拟合。

二、xGBoost

xGBoost的核心思想是，通过“泰勒展开”，将损失函数变为了 L = L’(yi,fm-1(xi)) * parameter + L’'(yi，fm-1(xi)) * parameter² + regularization 的形式。
从而使得parameter的求解可以通过解二次方程 ax² + bx 来得到(这里的parameter是一种Tree structure的叶子节点值）。
得到parameter后，我们既可计算出损失函数L。
对于每一轮Iteration中加入的Tree，我们可以通过损失函数来确定其具体结构，其step如下：

生成一棵depth=0的Tree；
从top到down，通过损失函数L来判断，叶子节点是否应该被split，其公式为：Gain = node_right + node_left - node + lambda < 0 ，说明node应该split，否则不split。这里，node_right指node的right分支的损失函数值，其它变量含义类似。

下面具体介绍xGBoost的工作原理：

首先不考虑xGBoost的model type，我们单纯考虑，其损失函数的定义，即定义xGBoost要优化的“目标函数”。在一般的损失函数定义中，往往包含2方面的内容：（1）我们希望由该损失函数优化获得的模型能够尽可能的拟合数据，即具有较小的bias；（2）我们希望由该损失函数优化得到的模型具有较好的泛化能力，即具有较小的variance。根据这2部分要求，我们可以将损失函数分解为2部分，一部分最小化bias，一部分抑制模型的复杂度，从而使其具有较好的泛化能力。根据这2部分，我们可以将损失函数定义为：
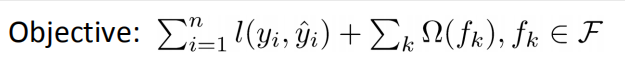
其前一部分为训练样本的平方和损失，后一部分为regularization，用于控制模型复杂度。
在定义了xGBoost损失函数类型以后，我们来定义xGBoost的抽象表达，由于xGBoost是一种Boost方法，其由若干个弱分类器组合而成，在xGBoost中，弱分类器为“回归树”。xGBoost可抽象表示为 yi^t = yi^t-1 + ft(xi)，其中ft(xi)为第t次iteration得到的弱分类器。yi^t-1为第t-1次得到的xGBoost模型的预测值，yi^t为第t次得到的xGBoost模型的预测值。
在定义完xGBoost的抽象表达后，下面我们来具体化损失函数的各个部分表达式：
首先，来看平方损失项：L^square = [yi - (yi^t-1 + ft(xi))]² = [(yi - yi^t-1)² + ft²(xi) + 2(yi^t-1 - yi)ft(xi)]，由于(yi - yi^t-1)²与待求函数ft(xi)无关，因此，我们将其舍去，平方损失变为：[2(yi^t-1 - yi)ft(xi) + ft²(xi)] 。
上述平方损失变形还可以通过泰勒公式展开得到，具体如下：
考虑利用泰勒公式，将L^square展开。
泰勒公式可表示为：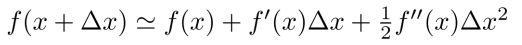
L^square = L(yi, yi^t-1 + ft(xi)) = L(yi, yi^t-1) + L’(yi, yi^t-1)ft(xi) +0.5 L’‘(yi, yi^t-1)*ft²(xi)，令gi = L’，hi = L’'。则L^square = L(yi, yi^t-1) + gi * ft(xi) + 0.5 * hi * ft²(xi)；
将gi = 2(yi - yi^t-1)，hi = 2，代入L^square，得： L^square = L(yi, yi^t-1) + 2(yi - yi^t-1) * ft(xi) + ft²(xi)；由于L(yi, yi^t-1) 为常数项，将其省略，则 L^square = 2(yi - yi^t-1) * ft(xi) + ft²(xi)；
上述是平方损失最后的化简形式，如果我们衡量biase的损失函数采用更为一般的损失函数时，则L^square = gi * ft(xi) + 0.5 * hi * ft²(xi)；
在定义完bias以后，接下来我们看regularization项的定义：
首先我们先定义ft(xi)的形式为：ft(xi) = wq(xi)，具体释义如下图所示：

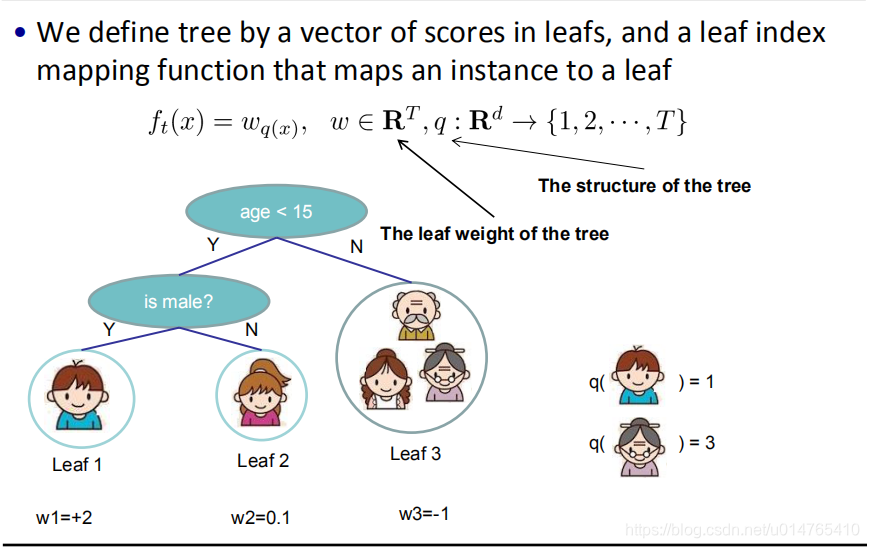
则regularization项可表示为如下形式：
通过第3步，我们定义了xGBoost各个部分的损失函数，现将损失函数重新组合为如下形式：

根据上述公式，我们即可以通过已知量 gi，hi，即“二次方程ax² + bx的求解公式”，求得给定Tree结构ft(xi)的情况下，ft(xi)中的w值，T为Tree中的结点个数；据此，我们可以求出给定Tree结构下的Obj^t。Obj^t代表第t次iteration中xGBoost模型的损失函数。
通过上述分析，我们好像已经求出了ft(xi)，但是，此时求得的ft(xi)是未经优化的Tree结构，那么我们如何获得ft(xi)的最优Tree结构呢，下一步将重点说明；
ft(xi)的Tree结构可以采用“后减枝”的策略获得，具体思路如下：
first. 先根据残差yi - yi^t-1 ，构建ft(xi);
second. 第一步构建的ft(xi)为一个depth=0的树根；
third. 根据损失函数Obj^t，求得一棵树分支与不分枝其损失函数的减小量D，我们将Gain = -D，Gain的具体计算公式，见如下几张PPT:

根据Gain 是否大于0，我们可以判断一个分枝是否合理：当Gain > 0时，保留分枝，否则，去除分枝；
通过上述步骤，已经确定了ft(xi)中，分枝的保留策略，根据这个策略，我们可以利用“决策树”的构造方式，来构建ft(xi)。
下面，给出“决策树” Best Spliting的寻找算法：
通过上述6步，可以求出一个最优的ft(xi)，每次iteration中，我们都可用同样的方法来求得一个f(xi)。为了保证得到的xGBoost不过拟合，我们可以给f(xi)定义一个shrinkage(0.1)，则 xGBoost = sum( shrinage * ft(xi) ) ,t=1,2,…,T。
通过以上步骤即可求得xGBoost模型。