|
Language:
Fibonacci
Description In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … An alternative formula for the Fibonacci sequence is
Given an integer n, your goal is to compute the last 4 digits of Fn. Input The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1. Output For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000). Sample Input 0 9 999999999 1000000000 -1 Sample Output 0 34 626 6875 Hint As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by
Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:
Source |
[Submit] [Go Back] [Status] [Discuss]
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define mod 10000
struct mat{
int A[3][3];
}s;
mat matmul(mat x,mat y) //x*y
{
mat t;
t.A[0][0]=(x.A[0][0]*y.A[0][0]+x.A[0][1]*y.A[1][0])%mod;
t.A[0][1]=(x.A[0][0]*y.A[0][1]+x.A[0][1]*y.A[1][1])%mod;
t.A[1][0]=(x.A[1][0]*y.A[0][0]+x.A[1][1]*y.A[1][0])%mod;
t.A[1][1]=(x.A[1][0]*y.A[0][1]+x.A[1][1]*y.A[1][1])%mod;
return t;
}
mat matpow(mat ss,int k) //ss^k
{
if(k==1) return s;
ss=matpow(ss,k/2);
if(k%2==0)
{
return matmul(ss,ss);
}
else
return matmul(matmul(ss,ss),s);
}
int main()
{
int i,j,n;
while(~scanf("%d",&n)&&n!=-1)
{
if(n==0)
{
printf("0\n");
continue;
}
s.A[0][0]=s.A[0][1]=s.A[1][0]=1;
s.A[1][1]=0;
s=matpow(s,n);
printf("%d\n",s.A[0][1]);
}
return 0;
}





 本文介绍如何使用矩阵快速幂算法高效地计算Fibonacci数列中任意项的最后四位数字,避免了传统的递归或迭代方法可能导致的性能瓶颈。
本文介绍如何使用矩阵快速幂算法高效地计算Fibonacci数列中任意项的最后四位数字,避免了传统的递归或迭代方法可能导致的性能瓶颈。
 .
.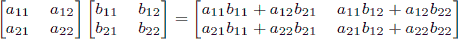 .
. .
.















 1112
1112

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








