Chessboard
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 14001 | Accepted: 4354 |
Description
Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the
figure below).
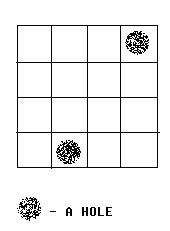
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:

A VALID solution.
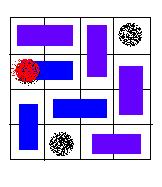
An invalid solution, because the hole of red color is covered with a card.
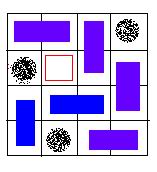
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:

A VALID solution.

An invalid solution, because the hole of red color is covered with a card.

An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.
Input
There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.
Output
If the board can be covered, output "YES". Otherwise, output "NO".
Sample Input
4 3 2 2 1 3 3
Sample Output
YES
题意:是否存在一种方式,使得用1*2的长方形覆盖所有空白区域。
思路:先判断空白区域是否为奇数,然后就是模板了。
AC代码如下:
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
int n,m,p,val[40][40],match[40][40][2],vis[40][40],VIS,dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
bool dfs(int x,int y)
{
int i,j,k,x2,y2;
for(i=0;i<4;i++)
{
x2=x+dx[i];y2=y+dy[i];
if(val[x2][y2]==0 && vis[x2][y2]!=VIS)
{
vis[x2][y2]=VIS;
if(match[x2][y2][0]==0 || dfs(match[x2][y2][0],match[x2][y2][1]))
{
match[x2][y2][0]=x;
match[x2][y2][1]=y;
return true;
}
}
}
return false;
}
int main()
{
int i,j,k,x,y,ret;
while(~scanf("%d%d%d",&n,&m,&p))
{
memset(val,0,sizeof(val));
for(i=1;i<=p;i++)
{
scanf("%d%d",&x,&y);
val[y][x]=1;
}
for(i=0;i<=n;i++)
val[i][0]=val[i][m+1]=1;
for(i=0;i<=m;i++)
val[0][i]=val[n+1][i]=1;
if((n*m-p)&1)
{
printf("NO\n");
continue;
}
ret=0;
memset(match,0,sizeof(match));
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
if((i+j)%2==0 && val[i][j]==0)
{
VIS++;
if(dfs(i,j))
ret++;
}
if(ret==(n*m-p)/2)
printf("YES\n");
else
printf("NO\n");
}
}







 本文探讨了一种利用1*2的矩形卡片覆盖带有洞孔的M*N大小棋盘的问题。文章提供了完整的AC代码实现,并介绍了如何通过深度优先搜索算法解决这一挑战。
本文探讨了一种利用1*2的矩形卡片覆盖带有洞孔的M*N大小棋盘的问题。文章提供了完整的AC代码实现,并介绍了如何通过深度优先搜索算法解决这一挑战。
















 1005
1005

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








