So Easy!
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 2089 Accepted Submission(s): 646
Problem Description
A sequence Sn is defined as:
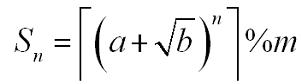
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate Sn.
You, a top coder, say: So easy!

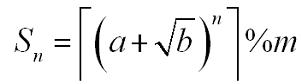
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate Sn.
You, a top coder, say: So easy!

Input
There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 215, (a-1)2< b < a2, 0 < b, n < 231.The input will finish with the end of file.
Output
For each the case, output an integer Sn.
Sample Input
2 3 1 2013 2 3 2 2013 2 2 1 2013
Sample Output
4 14 4
思路:所有的n次方我们都可以把它看成是a[n]+b[n]*根号b,然而a[n+1]=a*a[n]+b*b[n],b[n+1]=a[n]+a*b[b]。所以我们可以写出一个矩阵 a b 然后通过矩阵的相乘可以得到n次方式 a[n] 5*b[n]。
1 a b[n] a[n]
然后根据数论,因为由a和b的关系可以得到,这个答案应该是2*a。
AC代码如下:
#include<cstdio>
#include<cstring>
using namespace std;
struct node
{ long long mat[2][2];
};
node mat[4];
long long a,b,n,m,ans;
int b2[100],len;
void mul(int p)
{ int i,j,k;
memset(mat[3].mat,0,sizeof(mat[3].mat));
for(i=0;i<=1;i++)
for(j=0;j<=1;j++)
for(k=0;k<=1;k++)
mat[3].mat[i][j]=(mat[3].mat[i][j]+mat[1].mat[i][k]*mat[p].mat[k][j])%m;
for(i=0;i<=1;i++)
for(j=0;j<=1;j++)
mat[1].mat[i][j]=mat[3].mat[i][j];
}
void solve()
{ len=0;
memset(b2,0,sizeof(b2));
while(n)
{ len++;
if(n%2==1)
b2[len]=1;
n/=2;
}
while(--len)
{ if(b2[len]==0)
mul(1);
else
{ mul(1);
mul(2);
}
}
}
int main()
{ int i,j,k;
while(~scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&m))
{ mat[1].mat[0][0]=mat[2].mat[0][0]=a;
mat[1].mat[0][1]=mat[2].mat[0][1]=b;
mat[1].mat[1][0]=mat[2].mat[1][0]=1;
mat[1].mat[1][1]=mat[2].mat[1][1]=a;
solve();
ans=mat[1].mat[0][0]*2%m;
printf("%I64d\n",ans);
}
}








 本文介绍了一种利用矩阵快速幂高效计算特定形式序列的方法。针对给定的数学问题,通过对序列特性的分析,提出了使用矩阵乘法进行快速计算的策略,并给出了具体的实现代码。
本文介绍了一种利用矩阵快速幂高效计算特定形式序列的方法。针对给定的数学问题,通过对序列特性的分析,提出了使用矩阵乘法进行快速计算的策略,并给出了具体的实现代码。
















 7243
7243

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








