Matching Names（Trie树）-（VK Cup 2015 - Finals, online mirror）

A. Matching Names

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Teachers of one programming summer school decided to make a surprise for the students by giving them names in the style of the "Hobbit" movie. Each student must get a pseudonym maximally similar to his own name. The pseudonym must be a name of some character of the popular saga and now the teachers are busy matching pseudonyms to student names.

There are n students in a summer school. Teachers chose exactly n pseudonyms for them. Each student must get exactly one pseudonym corresponding to him. Let us determine the relevance of a pseudonym b to a student with name a as the length of the largest common prefix a and b. We will represent such value as 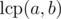. Then we can determine the quality of matching of the pseudonyms to students as a sum of relevances of all pseudonyms to the corresponding students.

Find the matching between students and pseudonyms with the maximum quality.

Input

The first line contains number n (1 ≤ n ≤ 100 000) — the number of students in the summer school.

Next n lines contain the name of the students. Each name is a non-empty word consisting of lowercase English letters. Some names can be repeating.

The last n lines contain the given pseudonyms. Each pseudonym is a non-empty word consisting of small English letters. Some pseudonyms can be repeating.

The total length of all the names and pseudonyms doesn't exceed 800 000 characters.

Output

In the first line print the maximum possible quality of matching pseudonyms to students.

In the next n lines describe the optimal matching. Each line must have the form a b (1 ≤ a, b ≤ n), that means that the student who was number a in the input, must match to the pseudonym number b in the input.

The matching should be a one-to-one correspondence, that is, each student and each pseudonym should occur exactly once in your output. If there are several optimal answers, output any.

Sample test(s)

input

5
gennady
galya
boris
bill
toshik
bilbo
torin
gendalf
smaug
galadriel

output

11
4 1
2 5
1 3
5 2
3 4

Note

The first test from the statement the match looks as follows:

• bill  →  bilbo (lcp = 3)
• galya  →  galadriel (lcp = 3)
• gennady  →  gendalf (lcp = 3)
• toshik  →  torin (lcp = 2)
• boris  →  smaug (lcp = 0)   

题意：给n个串，又给n个串，用前n个一一匹配后n个，求相同前缀字符数最多的匹配，及字符数（例子如上）。

思路：将id 1~n和n+1~2*n都录入trie树中，然后dfs从后向前匹配，深度越大优先匹配，匹配未被匹配的串。

//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<stdio.h>
#include<math.h>
#include <string>
#include<string.h>
#include<map>
#include<queue>
#include<set>
#include<utility>
#include<vector>
#include<algorithm>
#include<stdlib.h>
using namespace std;
#define eps 1e-8
#define inf 0x3f3f3f3f
#define rd(x) scanf("%d",&x)
#define rd2(x,y) scanf("%d%d",&x,&y)
#define ll long long int
#define mod 1000000007
#define maxn 900006
#define maxm 500010
int n,tot,res;
char s[maxn];
vector<int> ids[maxn];
int used[maxn];
pair<int,int> pp[maxn];
int pn;
vector<int> v1,v2;
struct node{
    int nt[26];
}trie[maxn];
int newnode(){//新建节点
    tot++;
    for(int i=0;i<26;i++) trie[tot].nt[i]=-1;
    return tot;
}
int gett(int x,char c){//获取节点编号
    if(trie[x].nt[c-'a']==-1) trie[x].nt[c-'a']=newnode();
    return trie[x].nt[c-'a'];
}
void Insert(char s[],int id){//插入trie树
    int now=0;
    ids[now].push_back(id);
    int len=strlen(s);
    for(int i=0;i<len;i++)
    {
        now=gett(now,s[i]);
        ids[now].push_back(id);
    }
}
int minn(int a,int b){
    return a<b?a:b;
}
void dfs(int x,int h){
    //if(x==-1) return;
    for(int i=0;i<26;i++)
        if(trie[x].nt[i]!=-1) dfs(trie[x].nt[i],h+1);
        v1.clear();v2.clear();
    for(int i=0;i<ids[x].size();i++)//获取该节点未匹配的串
    {
        int k=ids[x][i];
        if(used[k]) continue;
        if(k<=n) v1.push_back(k);
        else v2.push_back(k);
    }
    int k=minn(v1.size(),v2.size());//最多匹配k对
    for(int i=0;i<k;i++)
    {
        res+=h;
        used[v1[i]]=used[v2[i]]=1;
        pp[pn++]=make_pair(v1[i],v2[i]);
    }
}
int main()
{
    tot=-1;
    int rt=newnode();
    rd(n);
    for(int i=1;i<=2*n;i++)
    {
        scanf("%s",s);
        Insert(s,i);
    }
    pn=res=0;
    memset(used,0,sizeof(used));
    dfs(0,0);
    printf("%d\n",res);
    for(int i=0;i<n;i++)
    {
        printf("%d %d\n",pp[i].first,pp[i].second-n);
    }
    return 0;
}