机器学习的数学基础笔记P2-优快云博客

本文链接：https://blog.youkuaiyun.com/u014397365/article/details/139120453

偏导数

定义以及公式

偏导数

定义以及公式

着重要记住，偏导数的表达方式。

几何意义

例题

分别把x和y看成常数，然后求导，带入点，得到偏导数

方向导数

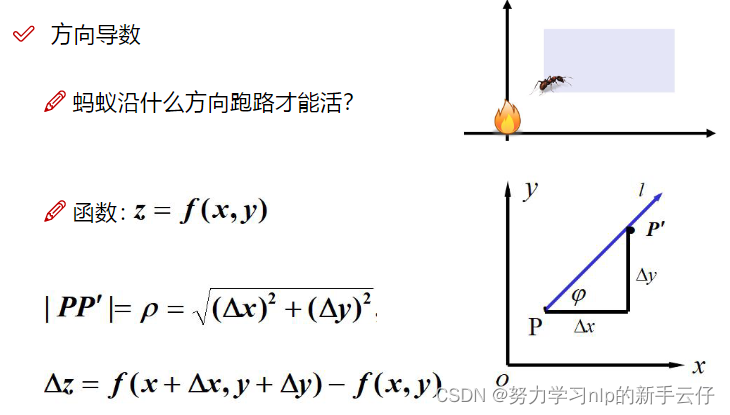
pp就算距离，也就是向量的长度，deltaz就算P点的值剪掉P的值

例题

梯度

例题

分别求出偏导，然后带入计算，得到距离。

小结

在机器学习中，梯度是一个极其重要的概念，尤其是在优化模型参数的过程中。梯度是函数在多维空间中的导数，它指向函数增长最快的方向。在机器学习中，我们通常关注的是损失函数（也称为代价函数）的梯度，因为我们的目标是最小化损失函数，以训练出性能良好的模型。

以下是梯度对于机器学习重要性的几个方面：

优化算法：梯度下降是最流行的优化算法之一，它利用损失函数的梯度来更新模型参数。通过沿着梯度的反方向（即梯度的负方向）调整参数，可以逐步减小损失函数的值，直到达到局部最小值或全局最小值。其他优化算法，如随机梯度下降（SGD）、Adam、RMSprop等，也是基于梯度的方法。
反向传播：在神经网络中，反向传播算法是一种计算损失函数关于每个参数的梯度的有效方法。这个算法通过链式法则，从输出层开始，逐层计算梯度，并用于更新网络的权重。反向传播是现代神经网络训练的基础。
性能分析：梯度不仅可以用于参数更新，还可以用于分析模型的性能。例如，梯度的大小可以提供关于学习率选择的信息：如果梯度太小，学习过程可能会太慢；如果梯度太大，可能会导致更新步骤过大，跳过最佳点。
正则化：在机器学习中，正则化是一种防止过拟合的技术。L2正则化（权重衰减）就是一个例子，它通过在损失函数中添加一个与参数大小成正比的项来实现。这个正则化项的梯度会影响参数的更新，有助于保持参数的大小适中。
模型诊断：梯度的大小和变化可以提供关于模型学习过程的诊断信息。例如，如果某些参数的梯度始终很小，可能意味着这些参数在模型中的作用不大，或者数据本身可能存在问题。
非线性优化：机器学习模型通常涉及到非线性函数的优化问题。梯度提供了这些非线性函数局部行为的信息，使得可以在复杂的参数空间中找到最优解。