快速排序
划分
- 给定一个数列A[lo...hi]
- 重排数列A[lo...hi],使其成为两个子数组(可能为空)A[lo...mi-1]和A[mi+1...hi]
对任何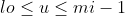 且
且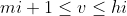 ,都有
,都有![A[u]< A[mi]< A[v]](https://i-blog.csdnimg.cn/blog_migrate/40a1df6c63c995edfcec0ce0028636ed.gif)
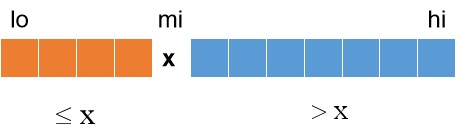
x称为轴(pivot)。
快速排序的步骤:
- 先调用划分
- 递归排序A[lo...mi-1]和A[mi+1...hi]
划分的思想:
使用A[hi]作为轴,从左向右扩展分区。

- 初始化(i,j) = (lo-1,lo)
- j每次加1,必要时i加1(当A[j] > x时,只增加j;当A[j] <= x时,还需增加i,并交换i,j号元素)
- 当j==hi时,结束
c++实现:
/**************************************************************
快速排序一次划分 (Partition)
时间复杂度:O(n)
备注:[lo,hi]为闭区间
***************************************************************/
int Partition(vector<int>& v, int lo, int hi)
{
int p = lo + rand()%(hi-lo+1); //随机取轴
//swap v[p] and v[hi]
int temp = v[p];
v[p] = v[hi];
v[hi] = temp;
int pivot = v[hi];
int i = lo - 1;
for(int j = lo; j < hi; ++j){
if(v[j] <= pivot){
++i;
//swap v[i] and v[j]
temp = v[i];
v[i] = v[j];
v[j] = temp;
}
}
//swap v[i+1] and v[hi]
temp = v[i+1];
v[i+1] = pivot;
v[hi] = temp;
return i+1;
}
/******************************************************************
快速排序 (QuickSort)
时间复杂度:O(nlogn)
备注:[lo,hi)为左闭右开区间
*******************************************************************/
void QuickSort(vector<int>& v, int lo, int hi)
{
if(hi - lo < 2) //单元素区间自然有序
return;
int mi = Partition(v,lo,hi-1);
QuickSort(v,lo,mi);
QuickSort(v,mi+1,hi);
}
堆排序
优先级队列
优先级队列是一种抽象数据结构,支持以下两种操作:
- 插入(Insert):插入堆新的元素
- 提取最小值(Extract-Min):从队列中移除并返回最小元素
二叉堆(Binary Heap):完全二叉树
堆序:A[parent(i)] <= A[i](最小堆)
堆的性质:
如果维持好堆序,堆可以高效支持以下两种操作:(假设队中有n个元素)
- 插入(Insert):O(logn)时间复杂度
- 提取最小值(Extract-Min):O(logn)时间复杂度
插入(Insertion)
- 插入新元素到堆末
- 恢复最小堆的性质(渗透:如果该元素的父节点比该元素更大,交换它们)
- 正确性:每次交换后,新元素为根的子树满足最小堆的性质
- 时间复杂度:O(logn)
提取最小值(Extract-Min)
- 复制最后元素到根
- 通过下渗透恢复最小堆的性质(如果该元素比它的两个孩子中之一更大,将该元素与较小的孩子交换)
- 正确性:每次交换后,除了包含该元素的节点外其他所有节点都满足最小堆的性质
- 时间复杂度:O(logn)
堆排序
- 构建一个n个元素的二叉堆(一个一个插入n个元素,更高效的方法见《算法导论》)
- 执行Extract-Min操作n次
c++实现:
/******************************************************************
堆插入(HeapInsert)
时间复杂度:O(logn)
备注1:v为最小堆,k为插入元素
备注2:堆数组从索引0开始,计算父子索引时略有改变
*******************************************************************/
void HeapInsert(vector<int>& v, int k)
{
v.push_back(k);
int i = v.size() - 1;
int p = (i - 1) / 2; //父节点索引
while (i > 0 && v[p] > v[i]) {
int temp = v[p];
v[p] = v[i];
v[i] = temp;
i = p;
p = (i - 1) / 2;
}
return;
}
/******************************************************************
提取最小值(Extract-Min)
时间复杂度:O(logn)
备注1:v为最小堆,返回堆顶元素
备注2:堆数组从索引0开始,计算父子索引时略有改变
*******************************************************************/
int ExtractMin(vector<int>& v)
{
int r = v[0];
int n = v.size();
v[0] = v[n - 1];
v.pop_back();
--n;
int i = 0;
int j = 2 * i + 1; //左子索引
while (j < n) { //存在左子
if (j < n - 1 && v[j] > v[j + 1]) //如果右子存在且较小
++j;
if (v[i] < v[j])
break;
else {
int temp = v[i];
v[i] = v[j];
v[j] = temp;
i = j;
j = 2 * i + 1;
}
}
return r;
}
/******************************************************************
堆排序(HeapSort)
先通过n次插入方式建堆,再n次提取堆顶元素排序
时间复杂度:O(nlogn)
*******************************************************************/
void HeapSort(vector<int>& v)
{
int n = v.size();
vector<int> t;
for (int i = 0; i < n; ++i)
HeapInsert(t, v[i]); //建堆
for (int i = 0; i < n; ++i)
v[i] = ExtractMin(t); //提取堆顶元素
return;
}
基于比较的排序算法的时间复杂度下界
基于比较的排序算法的时间复杂度下界: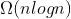 。(证明:决策树的高度)
。(证明:决策树的高度)
最快的排序算法
Which algorithm is the best in practice?
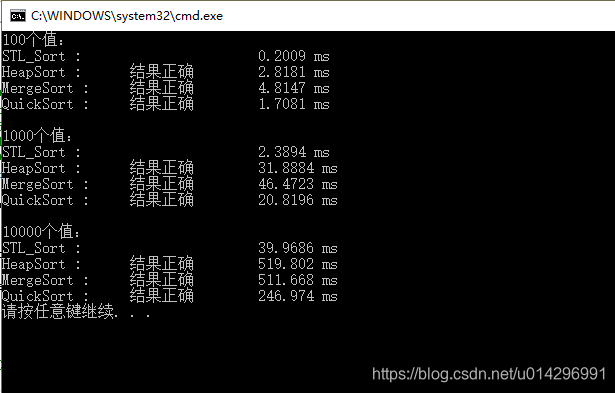
三种排序算法的运行时间对比可知:实际中,快速排序的用时最短,但与STL中实现的差距很大,可优化的空间还很大。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








