python3 实现线性回归(绘图说明)

线性回归实践

最新推荐文章于 2025-07-29 10:09:45 发布

置顶葡萄数

最新推荐文章于 2025-07-29 10:09:45 发布

阅读量1.2w

点赞数 8

CC 4.0 BY-SA版权

分类专栏：算法笔记文章标签：线性回归 numpy matplotlib

本文链接：https://blog.youkuaiyun.com/u013807136/article/details/83212287

算法笔记专栏收录该内容

13 篇文章

订阅专栏

本文介绍如何使用最小二乘法进行线性回归分析，通过生成线性相关数据集并预测y=2x+3的线性关系，展示了如何计算斜率和偏移值，最后用图表直观展示线性回归结果。

线性回归是最基本的预测, 先随机生成一堆大概线性相关的数据,

然后通过最小二乘法算出斜率和偏移值, 线性模型就能求出来了, 也能预测数据了

import numpy as np
import matplotlib.pyplot as plt

#数据集大小, 数据越多 a b就越准确

dataset_size = 100000
#干扰幅度, 干扰越小, ab越准确
amplitute = 200
#预测 y = 2x+3 的线性函数
x = np.random.randint(0,1000,dataset_size)
y = 2 * x + 3 + np.random.normal(size=dataset_size)*amplitute
print(x[:10])
print(y[:10])


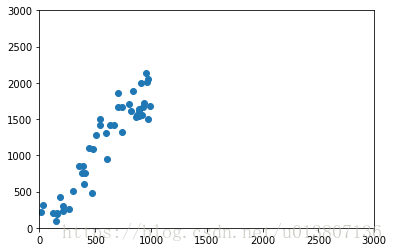
plt.scatter(x[:50],y[:50])
plt.axis([0,3000,0,3000])
plt.show()

输出结果: 
[865 603 390 894 593 818  18 304 402 708]
[ 1528.27202848   955.29457768   854.84928664  1621.34212968  1309.90961998
  1617.55872572   215.46963559   502.5849728    606.06870139  1862.69632193]

最小二乘法实现, 具体推到大家可以网上搜一下

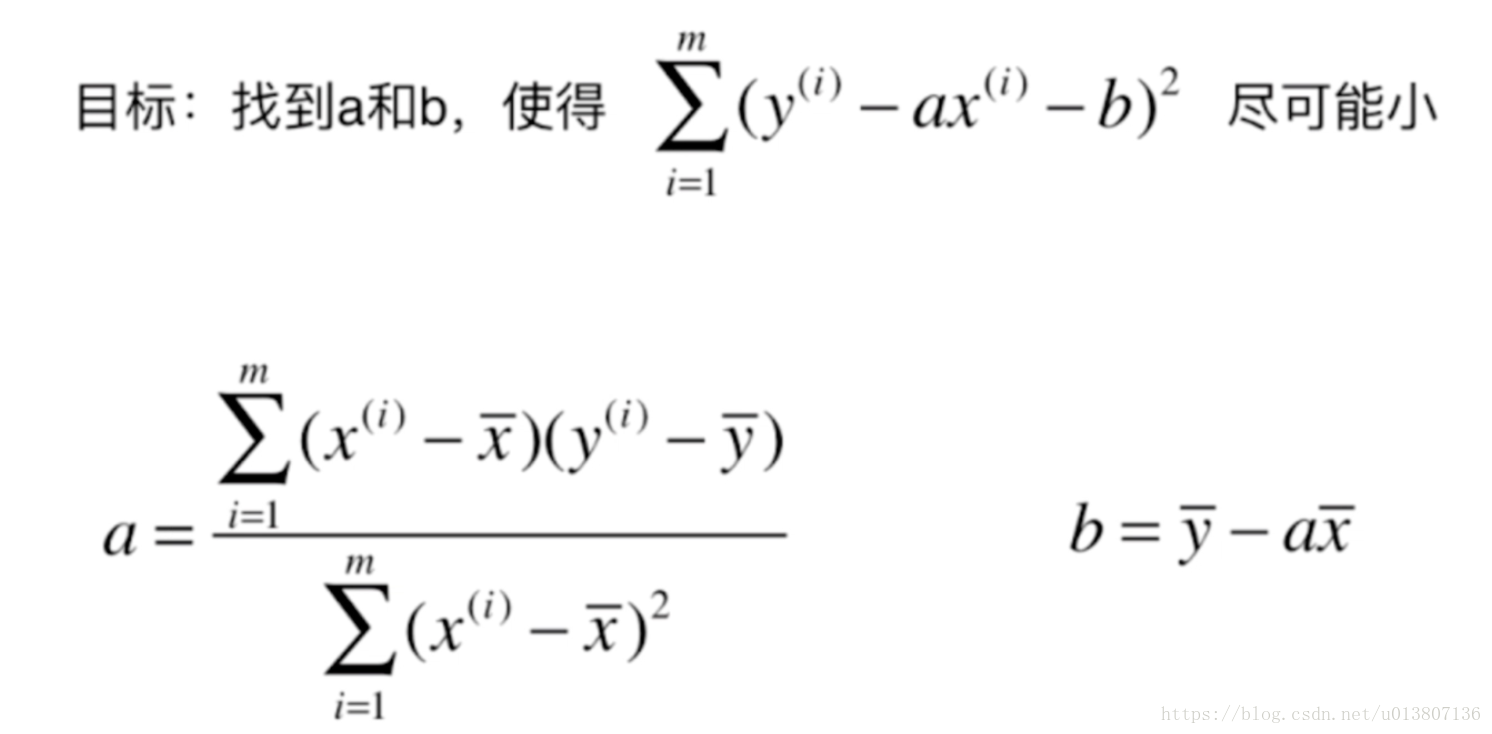
#这里使用最小二乘法求解线性回归的参数
x_mean = np.mean(x)
y_mean = np.mean(y)

m1 = 0   #分母
m2 = 0   #分子
for x_i, y_i in zip(x, y):
    m1 += (x_i - x_mean) * (y_i - y_mean)
    m2 += (x_i - x_mean) ** 2

a = m1/m2
b = y_mean - a*x_mean
print(a,b)

2.00067632091 3.07374278432

y_line = a*x + b
print(a,b)
plt.scatter(x[:50],y[:50])
plt.plot(x, y_line, color='r')
plt.axis([0,4000,0,4000])
plt.show()

2.00961672756 3.47528458815

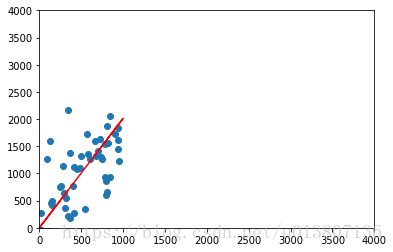
线性回归就完了