从虚数到八元数的数系边界延伸 |“虚构” 数系的数学特性与物理应用

注：本文为 “ ‘虚构’数系的特性与应用” 相关合辑。
英文引文，机翻未校。
略作重排，如有内容异常，请看原文。

---

The (Imaginary) Numbers at the Edge of Reality

（虚构的）现实边界之数

Odd enough to potentially model the strangeness of the physical world, complex numbers with “imaginary” components are rooted in the familiar.
带有“虚数”部分的复数虽奇特到有望模拟物理世界的怪异现象，却植根于我们熟悉的数系之中。

Have you ever sat in a math classroom and wondered, “When will I ever use this?” You might have asked yourself this question when you first encountered “imaginary” numbers, and with good reason: What could be less practical than a number described as imaginary?
你是否曾坐在数学课堂上疑惑：“我这辈子啥时候能用到这个？”第一次接触“虚数”时，你大概率问过自己这个问题——这很合理：还有什么比被称作“虚构”的数更不实用呢？

But imaginary numbers, and the complex numbers they help define, turn out to be incredibly useful. They have a far-reaching impact in physics, engineering, number theory and geometry. And they are the first step into a world of strange number systems, some of which are being proposed as models of the mysterious relationships underlying our physical world. Let’s take a look at how these unfamiliar numbers are rooted in the numbers we know, but at the same time, are unlike anything we have imagined.
但虚数及其助力定义的复数，实则用处极大。它们在物理、工程、数论和几何学中影响深远，更是通往一系列奇特数系世界的第一步——其中部分数系已被提议作为物理世界底层神秘关联的模型。让我们一同探究，这些陌生的数如何植根于我们熟知的数，却又与我们想象中的一切截然不同。

Real Numbers and Their Limitations

实数及其局限性

The “real numbers” are some of our most familiar mathematical objects: They are all the numbers that can be represented in decimal notation, like $5$, $8.2$, $-13.712$, $0$, $10.33333\dots$ and $\pi \approx 3.141592\dots$. We can add, subtract, multiply and divide real numbers, and we use them to answer questions both in classrooms and in our everyday lives. But the real numbers aren’t enough to solve all our math problems.
“实数”是我们最熟悉的数学对象之一：所有能以十进制表示的数都是实数，例如 $5$、$8.2$、$-13.712$、$0$、$10.33333\dots$ 以及 $\pi \approx 3.141592\dots$。我们可以对实数进行加减乘除运算，无论是课堂解题还是日常生活，都会用到它们。但实数并非能解决所有数学问题。

The Birth of Complex Numbers

复数的诞生

In the 1500s, the master equation solver Girolamo Cardano was trying to solve polynomial equations. He had no trouble solving equations like $x^2-8x+12=0$, because it was easy to find two numbers whose sum was $8$ and whose product was $12$: namely, $2$ and $6$. This meant $x^2-8x+12$ could be factored as $(x-2)(x-6)$, and expressing this polynomial as a product of two factors made solving the equation $x^2-8x+12=0$ easy.
16世纪，解方程大师吉罗拉莫·卡尔达诺（Girolamo Cardano）致力于求解多项式方程。对于 $x^2-8x+12=0$ 这类方程，他驾轻就熟——只需找到两个和为 $8$、积为 $12$ 的数（即 $2$ 和 $6$），就能将多项式 $x^2-8x+12$ 因式分解为 $(x-2)(x-6)$，而这种因式分解形式让方程求解变得简单。

But it wasn’t so easy to do this for equations like $x^2-3x+10=0$. Finding two numbers that add to $3$ and multiply to $10$ seems an impossible challenge. If the product of the two numbers is positive, they must have the same sign, and since their sum is positive, this means they must both be positive. But if two positive numbers add up to $3$, they must both be less than $3$, which means their product will be less than $3\times 3=9$. There doesn’t seem to be a way to make this work.
但对于 $x^2-3x+10=0$ 这类方程，情况就没这么简单了。找到两个和为 $3$、积为 $10$ 的数，简直是不可能完成的任务。若两数之积为正，则它们符号相同；又因两数之和为正，故两者必均为正数。但两个正数相加得 $3$，意味着它们都小于 $3$，其乘积自然小于 $3\times 3=9$，显然无法满足积为 $10$ 的要求。

Yet Cardano discovered that he could make it work, if he allowed himself to consider numbers that involved $\sqrt{-1}$, the square root of $–1$. It was a disturbing discovery. The square root of a number $k$, or $\sqrt{k}$, is the number that when multiplied by itself produces $k$. Now, when you square a real number, the result can never be negative: for example, $3\times 3=9$, $(-1.2)\times (-1.2)=1.44$ and $0\times 0=0$. This means no real number multiplied by itself could equal $–1$: Cardano was using $\sqrt{-1}$ to solve his real number equations, but $\sqrt{-1}$ isn’t itself a real number.
然而卡尔达诺发现，若允许引入含 $\sqrt{-1}$（即 $-1$ 的平方根）的数，问题便能迎刃而解。这一发现令人不安：数 $k$ 的平方根（记为 $\sqrt{k}$）是指自身相乘等于 $k$ 的数，而任意实数的平方都不可能为负数——例如 $3\times 3=9$、$(-1.2)\times (-1.2)=1.44$、$0\times 0=0$。这意味着没有任何实数的平方等于 $-1$：卡尔达诺用 $\sqrt{-1}$ 求解实数方程，但 $\sqrt{-1}$ 本身并非实数。

Properties of Complex Numbers

复数的性质

Cardano treated these non-real, or “imaginary,” numbers hesitantly, even describing the arithmetic he did with them as useless. But he was surprised to find that they obeyed many of the same rules that real numbers do. And although it took a while, Cardano’s reluctant use of $\sqrt{-1}$ led to the development of the “complex numbers,” a powerful and productive extension of the real numbers.
卡尔达诺对这些非实数（即“虚数”）的使用十分迟疑，甚至称相关运算毫无用处。但他意外发现，虚数遵循实数的诸多运算法则。尽管历经时日，卡尔达诺对 $\sqrt{-1}$ 的勉强使用，最终催生了“复数”——这一实数的强大且高效的扩展数系。

Complex numbers are made up of a real part and an imaginary part. They have the form $a+bi$, where $a$ and $b$ are both real numbers, and $i=\sqrt{-1}$, also known as the “imaginary unit.” They may seem strange at first, but we quickly find that we can add, subtract, multiply and divide complex numbers just as we do with real numbers.
复数由实部和虚部组成，形式为 $a+bi$，其中 $a$ 和 $b$ 均为实数，$i=\sqrt{-1}$ 被称为“虚数单位”。初看之下复数颇为怪异，但我们很快会发现，它们的加减乘除运算与实数并无二致。

Addition and Subtraction of Complex Numbers
复数的加减运算

To add and subtract complex numbers, you just combine the real parts and the imaginary parts, like this:
复数的加减运算只需合并实部与虚部，示例如下：

$$(5+3i)+(2+8i)=(5+2)+(3+8)i=7+11i$$

This is similar to combining “like terms” when you add polynomials together:
这与多项式加法中的“合并同类项”类似：

$$(3x+2)+(5x+7)=8x+9$$

Multiplication of Complex Numbers
复数的乘法运算

Multiplication of complex numbers is done using the same “distributive property” we use with real numbers. The distributive property tells us how multiplication and addition work together: For example, when you multiply $2$ and $(5+i)$, you distribute the $2$ over the sum of $5$ and $i$:
复数的乘法遵循实数的“分配律”——分配律描述了乘法与加法的联动关系。例如，计算 $2$ 与 $(5+i)$ 的乘积时，需将 $2$ 分配至 $5$ 和 $i$ 的和中：

$$2\times (5+i)=2\times 5+2\times i=10+2i$$

To multiply $2+3i$ and $5+i$, you just apply the distributive property twice. Here, the multiplication by $(5+i)$ is first distributed over the sum of $2$ and $3i$. That is:
计算 $2+3i$ 与 $5+i$ 的乘积时，需应用两次分配律：先将 $(5+i)$ 分配至 $2$ 和 $3i$ 的和中，即：

$$\begin{array}{rl}(2+3i)\times (5+i)& =2\times (5+i)+3i\times (5+i)\\ & =10+2i+15i+3i^2\\ & =10+17i+3i^2\end{array}$$

Notice that our answer, $10+17i+3i^2$, doesn’t have the form $a+bi$. Is this really a complex number, or is it something else? Here’s where we use the fact that $i^2=-1$.
注意到结果 $10+17i+3i^2$ 并非 $a+bi$ 的形式，它究竟是复数还是其他数？这就需要用到 $i^2=-1$ 的性质：

$$\begin{array}{rl}(2+3i)\times (5+i)& =10+17i+3i^2\\ & =10+17i+3(-1)\\ & =10+17i-3\\ & =7+17i\end{array}$$

Since we can write $10+17i+3i^2$ in the form $a+bi$, we know it is indeed a complex number. This illustrates the property of “closure”: When you multiply two complex numbers, you get another complex number. You don’t get something else.
由于 $10+17i+3i^2$ 可化为 $a+bi$ 的形式，因此它确实是复数。这体现了“封闭性”：两个复数相乘，结果仍为复数，不会得到其他类型的数。

Multiplication of complex numbers is even “commutative”: This means when you multiply two complex numbers in either order, the result is the same. For instance, you can verify that $(5+i)\times (2+3i)=7+17i$. We often take for granted that multiplication of real numbers is commutative — for example, that $5\times 4=4\times 5$ — but as we shall see later, this important fact doesn’t hold for every number system.
复数乘法还具有“交换性”：即两个复数相乘，交换顺序后结果不变。例如可验证 $(5+i)\times (2+3i)=7+17i$。我们通常认为实数乘法的交换性是理所当然的（如 $5\times 4=4\times 5$），但后续会发现，这一重要性质并非适用于所有数系。

Division of Complex Numbers

复数的除法运算

So we can multiply complex numbers, but how do we divide them? The key is understanding the relationship between division and multiplication.
既然复数可以相乘，那如何进行除法运算？关键在于理解除法与乘法的关联。

I often tell students that there is no such thing as division: There is only multiplication by the reciprocal. When we see the expression $\frac{10}{2}$, we usually think “$10$ divided by $2$,” but we can also think of this as $10\times \frac{1}{2}$, or “$10$ multiplied by the reciprocal of $2$.”
我常对学生说，其实不存在“除法”这一运算——只有“乘以倒数”。看到 $\frac{10}{2}$ 时，我们通常会想“$10$ 除以 $2$”，但也可以理解为 $10\times \frac{1}{2}$，即“$10$ 乘以 $2$ 的倒数”。

The reciprocal of a real, non-zero number $a$ is written $\frac{1}{a}$, and it is the unique number that, when multiplied by $a$, produces $1$. The reciprocal of $2$ is $\frac{1}{2}$, since $2\times \frac{1}{2}=1$. And it’s important to note that $\frac{1}{2}$ is a real number — you can write it as $0.5$ if you need to convince yourself.

实数 $a$（非零）的倒数写作 $\frac{1}{a}$，它是唯一一个与 $a$ 相乘后结果为 $1$ 的数。例如，$2$ 的倒数是 $\frac{1}{2}$，因为 $2\times \frac{1}{2}=1$。需要指出的是，$\frac{1}{2}$ 是一个实数——如果你需要说服自己，可以将其写成 $0.5$。

Now this may seem like an unnecessarily complicated approach to division, but it pays off when you start to think about numbers like $\frac{1}{i}$. The meaning of “$1$ divided by $i$” may not be immediately clear, but “the reciprocal of $i$” is the number you multiply with $i$ to get $1$. And it may be a little surprising that this number is $–i$!
这种除法思路看似复杂多余，但在处理 $\frac{1}{i}$ 这类数时却十分有效。“$1$ 除以 $i$”的含义或许并不直观，但“$i$ 的倒数”指的是与 $i$ 相乘得 $1$ 的数——而这个数竟是 $–i$，着实令人意外！

$$i\times (–i)=–(i\times i)=–(–1)=1$$

Using the fact that $i\times i=–1$, and some other important properties of real and complex numbers (that let us bring the negative sign out in front of the expression), we see that $i\times (–i)=1$, and so $–i$ really is the reciprocal of $i$. This means that if we ever want to divide a number by $i$, we can just multiply it by $–i$ instead.
利用 $i\times i=–1$ 这一性质，以及实数和复数的其他重要性质（允许将负号提到表达式前方），可推出 $i\times (–i)=1$，因此 $–i$ 确实是 $i$ 的倒数。这意味着，若要将某个数除以 $i$，只需将其乘以 $–i$ 即可。

For other complex numbers, the arithmetic may get a little harder, but the reciprocal idea still works. For example, to compute $\frac{1+2i}{3+4i}$ we need to find the reciprocal of $3+4i$, and to do that we’ll use a trick involving the “conjugate” of a complex number — that is, the number you get when you switch the sign of its imaginary part.
对于其他复数，运算可能稍复杂，但倒数的思路依然适用。例如计算 $\frac{1+2i}{3+4i}$ 时，需先求 $3+4i$ 的倒数，这里要用到复数“共轭”的技巧——共轭指的是将复数虚部的符号反转后得到的数。

Notice what happens when we multiply the complex number $3+4i$ by its conjugate $3–4i$. That is:
观察复数 $3+4i$ 与其共轭 $3–4i$ 的乘积，即：

$$\begin{array}{rl}(3+4i)\times (3-4i)& =3\times (3-4i)+4i\times (3-4i)\\ & =3\times 3-3\times 4i+4i\times 3-4i\times 4i\\ & =9-12i+12i-16i^2\\ & =9-16i^2\\ & =9+16\\ & =25\end{array}$$

The product of the complex number and its conjugate is a real number! This is true in general, since $(a+bi)\times (a-bi)=a^2+b^2$ and $a$ and $b$ are always real numbers.
复数与其共轭的乘积是实数！这是普遍规律，因为 $(a+bi)\times (a-bi)=a^2+b^2$，而 $a$ 和 $b$ 均为实数。

This property of conjugates helps us compute the reciprocal of any complex number. Since $(3+4i)\times (3–4i)=25$, we divide both sides of the equation by $25$ and do some algebra:
共轭的这一性质可帮助我们求任意复数的倒数。由于 $(3+4i)\times (3–4i)=25$，将等式两边同时除以 $25$ 并整理：

$$\begin{array}{rl}(3+4i)\times (3-4i)& =25\\ \frac{(3+4i)\times (3-4i)}{25}& =\frac{25}{25}\\ \frac{(3+4i)\times (3-4i)}{25}& =1\\ (3+4i)\times \frac{(3-4i)}{25}& =1\end{array}$$

Since $(3+4i)$ and $\frac{(3-4i)}{25}$ multiply to $1$, we know $\frac{(3-4i)}{25}$ is the reciprocal of $(3+4i)$. When we want to divide by $(3+4i)$, we just multiply instead by $\frac{(3-4i)}{25}$. So to compute $\frac{1+2i}{3+4i}$, we multiply:
由于 $(3+4i)$ 与 $\frac{(3-4i)}{25}$ 的乘积为 $1$，因此 $\frac{(3-4i)}{25}$ 是 $(3+4i)$ 的倒数。若要除以 $(3+4i)$，只需乘以 $\frac{(3-4i)}{25}$。因此计算 $\frac{1+2i}{3+4i}$ 时，运算如下：

$$\frac{1+2i}{3+4i}=(1+2i)\times \frac{(3-4i)}{25}=\frac{11+2i}{25}$$

Beyond Complex Numbers: Quaternions and Octonions

超越复数：四元数与八元数

The introduction of this one new non-real number — $i$, the imaginary unit — launched an entirely new mathematical world to explore. It is a strange world, where squares can be negative, but one whose structure is very similar to the real numbers we are so familiar with. And this extension to the real numbers was just the beginning.
引入 $i$ 这一全新的非实数（虚数单位），开启了一个亟待探索的全新数学世界。这个世界虽奇特（平方可为负数），但其结构与我们熟知的实数极为相似。而对实数的这一扩展，仅仅是个开始。

In 1843, William Rowan Hamilton imagined a world in which there were many distinct “imaginary units,” and in doing so discovered the quaternions. The quaternions are structured like the complex numbers, but with additional square roots of $–1$, which Hamilton called $j$ and $k$. Every quaternion has the form $a+bi+cj+dk$, where $a$, $b$, $c$ and $d$ are real numbers, and $i^2=j^2=k^2=-1$. You might think anyone can invent a new number system, but it’s important to ask if it will have the structures and properties we want. For instance, will the system be closed under multiplication? Will we be able to divide?
1843年，威廉·罗恩·哈密顿（William Rowan Hamilton）构想了一个存在多个不同“虚数单位”的世界，并由此发现了四元数。四元数的结构与复数类似，但新增了 $–1$ 的另外两个平方根，哈密顿将其命名为 $j$ 和 $k$。每个四元数的形式为 $a+bi+cj+dk$，其中 $a$、$b$、$c$、$d$ 均为实数，且满足 $i^2=j^2=k^2=-1$。你或许会认为任何人都能发明新数系，但关键在于它是否具备我们所需的结构和性质——例如，是否满足乘法封闭性？能否进行除法运算？

To ensure the quaternions had these properties, Hamilton had to figure out what to do about $i\times j$. All quaternions need to look like $a+bi+cj+dk$, and $i\times j$ doesn’t. We ran into a similar problem when we first multiplied two complex numbers: Our initial result had an $i\times i$ term in it, which didn’t seem to fit. Luckily, we could use the fact that $i^2=-1$ to put the number in its proper form. But what can be done with $i\times j$?
为确保四元数具备这些性质，哈密顿必须解决 $i\times j$ 的运算结果问题。所有四元数都需符合 $a+bi+cj+dk$ 的形式，但 $i\times j$ 显然不满足。这与我们最初计算两个复数相乘时遇到的问题类似：初始结果中出现了 $i\times i$ 项，看似不符合标准形式，但幸运的是，我们可以利用 $i^2=-1$ 将其化为规范形式。可 $i\times j$ 该如何处理呢？

Hamilton himself struggled to understand this product, and when the moment of inspiration finally came, he carved his insight into the stone of the bridge he was crossing:
哈密顿本人曾长期困惑于这一乘积的结果，直到灵感迸发的那一刻——他将自己的发现刻在了途经的桥面上：

$$i^2=j^2=k^2=i\times j\times k=-1$$

People from all over the world still visit Broome Bridge in Dublin to share in this moment of mathematical discovery.
如今，仍有世界各地的人们前往都柏林的布鲁姆桥（Broome Bridge），缅怀这一数学发现的瞬间。

Hamilton’s famous relationship between the imaginary units $i$, $j$ and $k$ allows us to multiply and divide quaternions and get the results we mostly expect. Let’s see how this resolves the question of what $i\times j$ should be.
哈密顿发现的虚数单位 $i$、$j$、$k$ 之间的著名关系，让四元数的乘除运算能够得到符合预期的结果。下面我们来看看它如何确定 $i\times j$ 的值。

Starting with $i\times j\times k=–1$, we multiply both sides of the equation (on their right sides) by $k$ and simplify.
从 $i\times j\times k=–1$ 出发，将等式两边（右侧）同时乘以 $k$ 并化简：
$$\begin{array}{rl}i\times j\times k& =-1\\ (i\times j\times k)\times k& =-1\times k\\ (i\times j)\times (k\times k)& =-k\\ (i\times j)\times (-1)& =-k\\ -(i\times j)& =-k\\ i\times j& =k\end{array}$$

From Hamilton’s relationship, we see that $i\times j=k$. Here we are using the fact that $k\times k=–1$ along with other properties, including the “associative property” of multiplication, which says that, when multiplying more than two things together, you can choose which pair to multiply first. This is another property we take for granted with the real numbers — for example, $(2\times 3)\times 10=2\times (3\times 10)$ — and as with commutativity, we will see it doesn’t always hold for every number system.
由哈密顿的关系式可知 $i\times j=k$。此处用到了 $k\times k=–1$ 的性质，以及乘法的“结合律”——即多个数相乘时，可任意选择先计算其中一对的乘积。这是我们对实数习以为常的另一性质（例如 $(2\times 3)\times 10=2\times (3\times 10)$），但和交换律一样，它并非适用于所有数系。

The other products can be derived in a similar way, and so we get a multiplication table of imaginary units that looks like this:
其他乘积可通过类似方法推导得出，由此得到虚数单位的乘法表如下：

$$\begin{gathered} i\times j=kj\times k=ik\times i=j \\ j\times i=–kk\times j=–ii\times k=–j \end{gathered}$$

These quaternion multiplication rules can be represented in the following diagram:
四元数的乘法规则可通过下图直观表示：

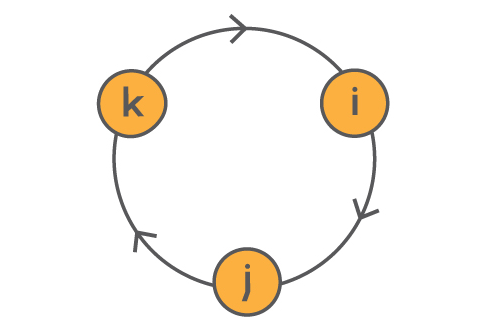
Here, moving around the circle in the direction of the arrows gives you the appropriate product ($i\times j=k$), and moving in the opposite direction introduces a factor of $–1$ (ex. $j\times i=–k$).
沿图中箭头方向绕圆移动，可得到对应乘积（如 $i\times j=k$）；沿反方向移动，则结果需乘以 $–1$（例如 $j\times i=–k$）。

Notice this means that, unlike with the real and complex numbers, multiplication of quaternions is not commutative. (This is why we had to multiply both sides of the equation $i\times j\times k=–1$ above by $k$ on their right sides.) Multiplying two quaternions in different orders may produce different results!
需注意，与实数和复数不同，四元数的乘法不满足交换律（这也是前文需将等式 $i\times j\times k=–1$ 两边右侧同时乘以 $k$ 的原因）。两个四元数交换相乘顺序，结果可能不同！

$$\{\begin{array}{l}i\times j=k\\ \ne \\ j\times i=-k\end{array}$$

To get the kind of structure we want in the quaternions, we have to abandon the commutativity of multiplication. This is a real loss: Commutativity is a kind of algebraic symmetry, and symmetry is always a useful property in mathematical structures. But with these relationships in place, we gain a system where we can add, subtract, multiply and divide much as we did with complex numbers.
要让四元数具备我们所需的结构，就必须舍弃乘法交换律。这是一种实实在在的牺牲——交换律是一种代数对称性，而对称性在数学结构中始终是有用的性质。但有了这些关系式，我们便得到了一个可像复数一样进行加减乘除运算的数系。

To add and subtract quaternions, we collect like terms as before. To multiply we still use the distributive property: It just requires a little more distributing. And to divide quaternions, we still use the idea of the conjugate to find the reciprocal, because just as with complex numbers, the product of any quaternion with its conjugate is a real number.
四元数的加减运算仍需合并同类项；乘法运算仍遵循分配律，只是需多步分配；除法运算则仍利用共轭求倒数——因为与复数类似，任意四元数与其共轭的乘积为实数：

$$(a+bi+cj+dk)\times (a-bi-cj-dk)=a^2+b^2+c^2+d^2$$

For example, if we want to divide by the quaternion $1+i+j+k$, we use the fact that $(1+i+j+k)(1–i–j–k)=4$, which allows us to find the reciprocal of $1+i+j+k$, namely:
例如，若要除以四元数 $1+i+j+k$，可利用 $(1+i+j+k)(1–i–j–k)=4$ 这一性质，求得 $1+i+j+k$ 的倒数为：

$$\frac{1}{1+i+j+k}=\frac{1-i-j-k}{4}$$

Thus, the quaternions are an extension of the complex numbers where we can add, subtract, multiply and divide. And like the complex numbers, the quaternions are surprisingly useful: They can be used to model the rotation of three-dimensional space, which makes them invaluable in rendering digital landscapes and spherical video, and in positioning and orienting objects like spaceships and cellphones in our three-dimensional world.
因此，四元数是复数的扩展数系，可进行加减乘除运算。且与复数一样，四元数的实用性令人意外：它能用于模拟三维空间的旋转，因此在数字景观渲染、球面视频制作，以及宇宙飞船、手机等物体在三维空间中的定位与定向方面，具有不可替代的作用。

The Strange World of Octonions

八元数的奇妙世界

These extensions beyond the real numbers continue still with the eight-dimensional octonions, an even stranger number system discovered by Hamilton’s colleagues that has seven imaginary units. Just as in all the other number systems we’ve seen, you can add, subtract, multiply and divide octonions. And just as with the quaternions, we need some special rules to govern how to multiply all the imaginary units. Here they are, represented graphically in a diagram known as the “Fano plane”:
对实数的扩展并未止步于四元数，接下来是八维的八元数——这是哈密顿的同事发现的一种更奇特的数系，包含七个虚数单位。与我们之前介绍的所有数系一样，八元数可进行加减乘除运算；且与四元数类似，其虚数单位的乘法需遵循特殊规则，这些规则可通过名为“法诺平面”（Fano plane）的图形直观表示：

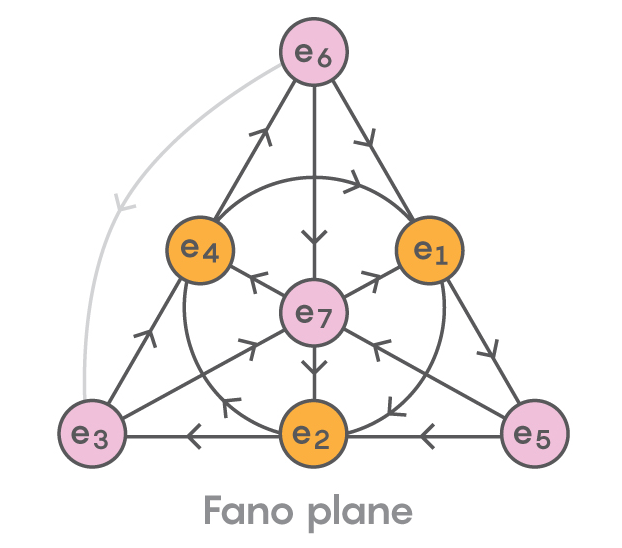
As in the representation for the quaternions, multiplying along the direction of the arrow gives a positive product, and against the arrow gives a negative one.
与四元数的表示方法相同，沿箭头方向相乘结果为正，逆箭头方向相乘结果为负。

Like the quaternions, octonion multiplication is not commutative. But extending our idea of number out to the octonions costs us the associativity of multiplication as well. When multiplying three octonions $x$, $y$ and $z$, it’s not necessarily true that $(x\times y)\times z=x\times (y\times z)$. For example, using the diagram above, we can see that
与四元数一样，八元数的乘法不满足交换律。但将数系扩展至八元数，我们还需舍弃乘法结合律：对于三个八元数 $x$、$y$、$z$，$(x\times y)\times z=x\times (y\times z)$ 不一定成立。例如，根据上图可得出：

$$\begin{array}{rlr}& (e_3\times e_4)\times e_1& =e_6\times e_1=e_5\\ & \text{but}& \\ & e_3\times (e_4\times e_1)& =e_3\times e_2=-e_5\end{array}$$

So now we have a number system with non-commutative, non-associative multiplication and seven square roots of $-1$. When would anyone ever use that? Well, some physicists believe that the octonions may hold the key to describing how the strong, weak and electromagnetic forces act on quarks, leptons and their anti-particles. If true, this could help resolve one of the great mysteries in modern physics.
至此，我们得到了一个乘法既不满足交换律也不满足结合律、且存在七个 $-1$ 平方根的数系。这样的数系何时会被用到？部分物理学家认为，八元数可能是描述强相互作用、弱相互作用和电磁相互作用如何作用于夸克、轻子及其反粒子的关键。若情况属实，这或许能帮助解开现代物理学中的一大谜团。

By repeatedly extending the real numbers to create larger systems — the complex numbers, the quaternions, the octonions — in which we can add, subtract, multiply and divide, we lose a little familiarity with each step. Along the way, we may also lose touch with what we think of as real. But what we gain are new ways of thinking about the world. And we can always find a use for that.
通过不断扩展实数，我们构建了复数、四元数、八元数等更大的数系——它们均支持加减乘除运算，但每一步扩展都让我们远离了熟悉的领域，甚至可能脱离我们对“真实”的认知。但与此同时，我们获得了思考世界的新视角，而这样的视角总能找到其用武之地。

Exercises

习题

1. We created the complex numbers by defining $i$ so that $i^2=-1$. Can you find a complex number $z$ such that $z^2=i$?
   Hint: Let $z=a+bi$ and square it. Under what conditions on $a$ and $b$ would this be equal to $i$?
   我们通过定义 $i^2=-1$ 构建了复数系。能否找到一个复数 $z$，使得 $z^2=i$？
   提示：设 $z=a+bi$ 并对其平方，分析 $a$ 和 $b$ 需满足何种条件才能使结果等于 $i$？

2. Let $z=\frac{1}{2}+\frac{\sqrt{3}}{2}i$. Show that $z^3=-1$. Can you find the other two cube roots of $–1$?
   设 $z=\frac{1}{2}+\frac{\sqrt{3}}{2}i$，证明 $z^3=-1$，并找出 $–1$ 的另外两个立方根。

Correction added Oct. 26: William Rowan Hamilton’s middle name was misspelled as “Rohan” in the original post of this article.
10 月 26 日更正说明：原文中威廉·罗恩·哈密顿（William Rowan Hamilton）的中间名误写为“Rohan”。

---

Four Special Number Systems

四种特殊的数系

Revised July 22, 2018 Quanta Magazine

When you add, subtract, multiply or divide the “real numbers” used in everyday life, you always get another real number. Three generalizations of the real numbers also behave in this way. Many physicists believe that all four of these “division algebras” underlie the laws of physics.
当对日常生活中使用的 “实数” 进行加、减、乘、除运算时，结果始终是另一个实数。实数的三种推广形式也具有这一特性。许多物理学家认为，这四种 “可除代数” 构成了物理定律的数学基础。

Real numbers 实数

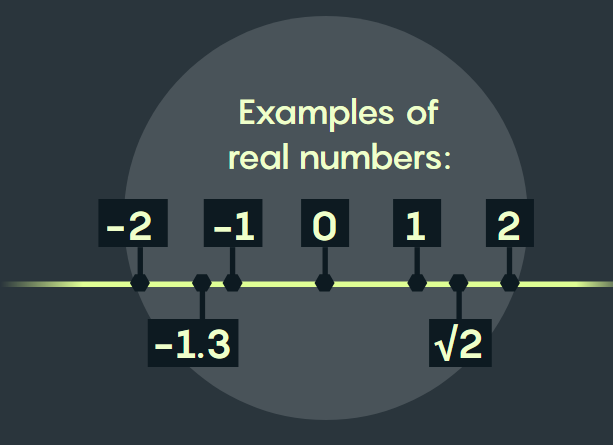
All the numbers on (1-D) number line are real numbers. One defining characteristic of reals is that their square is never negative. For example, $2^2=4$ and also $(-2{)}^2=4$.
所有位于一维数轴上的数均为实数。实数的一个定义性特征是其平方非负。例如，$2^2=4$，同样 $(-2{)}^2=4$。

Examples of real numbers: $0,-1,1$
实数示例：$0,-1,1$

Complex numbers 复数

One defining characteristic of $i$ is that its square is negative, i.e., $i^2=-1$. Reals are used in conjunction with an unconventional “imaginary” unit called $i$.
虚数单位 $i$ 的一个定义性特征是其平方为负，即 $i^2=-1$。实数与这一特殊的 “虚数单位”$i$ 结合构成复数体系。

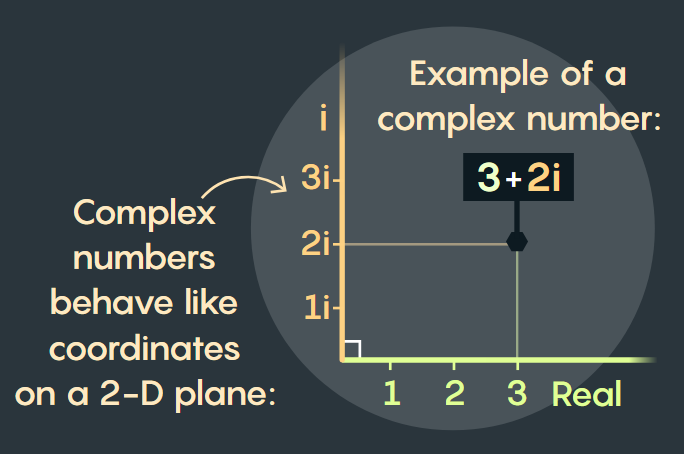
Example of a complex number: $3+2i$
复数示例：$3+2i$

Quaternions 四元数

Reals are used in conjunction with three unconventional units called $i,j$, and $k$.
实数与三个特殊单位 $i、j$ 和 $k$ 结合构成四元数体系。

Multiplication of quaternions is noncommutative: Swapping the order of elements changes the result.
四元数的乘法满足不可交换性：交换元素的运算顺序会改变结果。

Quaternions behave like coordinates in 4-D space:
四元数的性质类似于四维空间中的坐标：

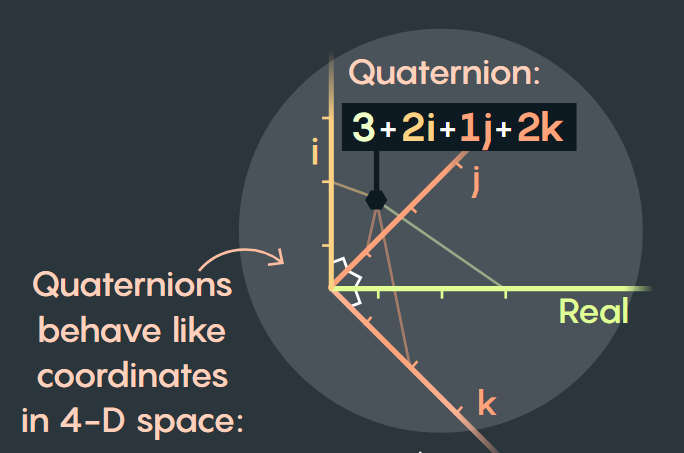
Multiplication follows a cyclic pattern, where multiplying neighboring elements results in the third:
其乘法遵循循环规律，相邻元素相乘得到第三个元素：

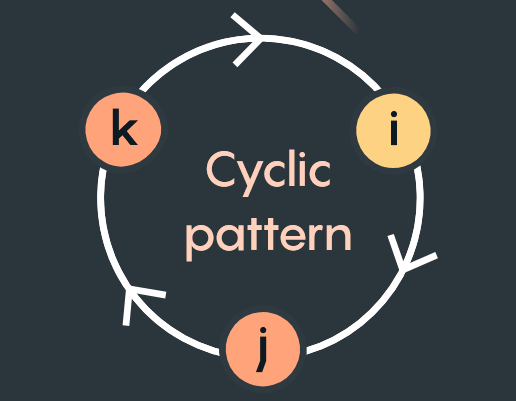
Moving with arrows gives a positive answer:
按箭头方向运算得正结果：
$i\times j=k$；

moving against arrows gives a negative answer:
逆箭头方向运算得负结果：
$j\times i=-k$。

Octonions 八元数

Reals are used in conjunction with seven unconventional units: $e_1,e_2,e_3,e_4,e_5,e_6$, and $e_7$ (where $e_1,e_2$, and $e_4$ are comparable to the quaternions’ $i,j$, and $k$).
实数与七个特殊单位 $e_1、e_2、e_3、e_4、e_5、e_6$ 和 $e_7$ 结合构成八元数体系（其中 $e_1、e_2$ 和 $e_4$ 分别对应四元数中的 $i、j$ 和 $k$）。

Example of an octonion:
八元数示例：
$$3+2e_1+2e_2+3e_3+2e_4+2e_5+1e_6+3e_7$$

Octonions behave like coordinates in 8-D space. Their multiplication rules are encoded in the “Fano plane.” Multiplying two neighboring elements on a line results in the third element on that same line. Imagine additional lines that close the loop for each group of three elements (e.g., the dashed lines).
八元数的性质类似于八维空间中的坐标。其乘法规则可通过 “法诺平面” 表征：同一直线上的两个相邻元素相乘，结果为该直线上的第三个元素。可将额外的线（如虚线）理解为闭合每组三个元素的循环路径。

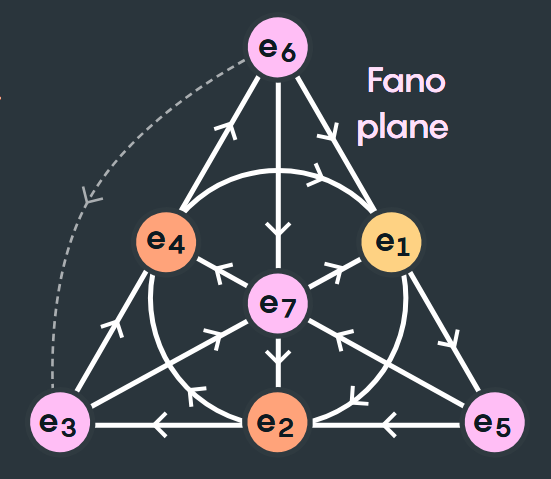
Moving with arrows gives a positive answer: e.g.,
按箭头方向运算得正结果：例如
$e_5\times e_2=e_3$ and $e_6\times e_3=e_4$;

moving against arrows gives a negative answer: e.g.,
逆箭头方向运算得负结果：例如
$$\begin{array}{rl}& e_1\times e_7=-e_3\\ & \text{and}\\ & e_6\times e_5=-e_1\end{array}$$

To see their nonassociative property, multiply three elements $e_5,e_2,e_4$.
八元数的非结合性可通过以下运算验证：取三个元素 $e_5、e_2、e_4$ 相乘，

Grouping them like this $(e_5\times e_2)\times e_4=(e_3)\times e_4=e_6$.
按 $(e_5\times e_2)\times e_4=e_3\times e_4=e_6$ 分组运算，

But grouping them like this $e_5\times (e_2\times e_4)=e_5\times (e_1)=-e_6$. Different answers.
与按 $e_5\times (e_2\times e_4)=e_5\times e_1=-e_6$ 分组运算，结果不同。

---

各数系性质对比表

数系	维度	构成形式	虚数单位数量	乘法交换律	乘法结合律	典型应用场景
实数	1	单一实部 （如 $a$）	0 个	满足	满足	日常计算、基础数学问题求解
复数	2	实部 + 虚部 （$a+bi$）	1 个 （$i$）	满足	满足	物理建模、工程计算、几何学分析
四元数	4	实部 + 三个虚部 （$a+bi+cj+dk$）	3 个 （$i,j,k$）	不满足	满足	三维空间旋转模拟、数字渲染、物体定位定向
八元数	8	实部 + 七个虚部 （$a+e_1{x}_1+\cdots +e_7{x}_7$）	7 个 （$e_1-e_7$）	不满足	不满足	粒子物理研究、强 / 弱 / 电磁相互作用描述探索

---

via:

• The (Imaginary) Numbers at the Edge of Reality
  https://www.quantamagazine.org/the-imaginary-numbers-at-the-edge-of-reality-20181025/

• Four Special Number Systems - NumberSystems.pdf
  https://www.quantamagazine.org/wp-content/uploads/2018/10/NumberSystems.pdf