注:本文为 “基波、载波与谐波” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
基波、载波、谐波
飞翔灬鲨鱼 原创于 2021-10-25 16:18:31 发布
基波、载波、谐波
-
载波或载频(载波频率)
载波是一个物理概念,指特定频率的无线电波,单位为 Hz \text{Hz} Hz。它是一种在频率、调幅或相位维度上被调制,以传输语言、音乐、图像或其他信号的电磁波。在无线通信技术中,载波用于传递信息:将数字信号调制到高频载波上,再通过空中进行发射与接收。因此,载波是传送信息(话音与数据)的物理基础,也是信息的最终承载工具。形象地说,载波可类比为一列火车,用户信息则对应火车所装载的货物。 -
基波
在复杂的周期性振荡中,其信号成分包含基波和谐波。与该振荡最长周期相等的正弦波分量被定义为基波,对应于这一周期的频率称为基波频率或基本频率。 -
谐波
频率等于基本频率整数倍的正弦波分量称为谐波。具体而言,谐波是对周期性非正弦交流量进行傅里叶级数分解后,所得到的频率大于基波频率整数倍的各次分量,通常也称为高次谐波;而基波特指频率与工频( 50 Hz 50\ \text{Hz} 50 Hz)相同的分量。在当前电力系统中,高次谐波的干扰是影响电能质量的主要“公害”之一,亟需采取针对性抑制措施。
谐波的产生原因
谐波产生的原因是正弦电压施加于非线性负载时,基波电流发生畸变,进而生成谐波。常见的非线性负载包括 UPS、开关电源、整流器、变频器、逆变器等电力电子设备。
谐波与泛音的区别
泛音在物理学范畴内属于谐波,但二者在次数定义上存在差异:基波频率 2 倍的音频称为一次泛音,基波频率 3 倍的音频称为二次泛音,以此类推;而谐波的次数定义为“频率与基波频率的倍数”,即基波频率 3 倍的波称为三次谐波,基波频率 5 倍的波称为五次谐波,以此类推。需注意,无论次数高低,谐波的波形均为正弦波。
基波与谐波
一个小白的硬件工程师成长 原创于 2023-07-01 17:03:33 发布
基波与谐波
在振动学理论中,一个振动所产生的波包含一个具有特定频率且振幅最大的正弦波,该正弦波被定义为基波;而在同一振动产生的波中,所有频率高于基波频率、且振幅小于基波振幅的小波,均称为谐波。
如图 1.1 右图所示,现实场景中各类信号的实际波形(图中黑色曲线)均为畸变波形,其中基波成分可通过“振幅最大、频率固定”的特征直接识别,但谐波成分无法直接观测。
如图 1.1 左图所示,该图为对右图畸变波形进行傅里叶级数分解后的结果:图中黑色曲线为基波,其频率最低、幅值最大;灰色曲线为各次谐波分量,其频率均为基波频率的整数倍。
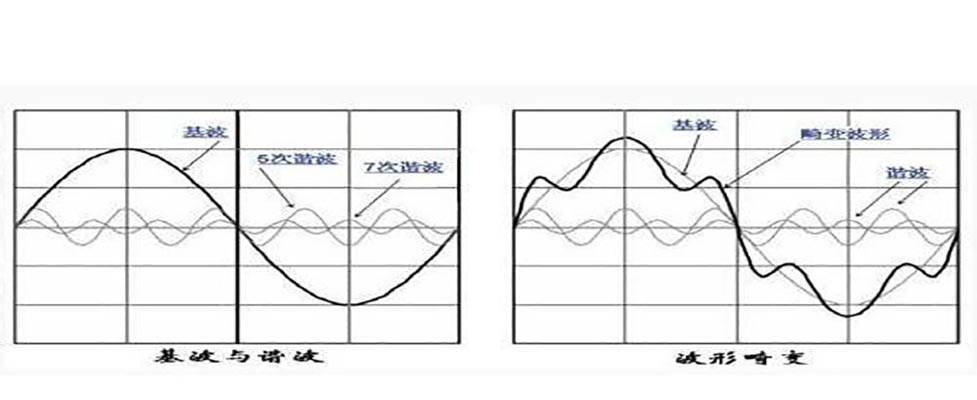
图 1.1 基波与谐波的关系(左) 实际畸变的波形(右)
谐波的定义
谐波是对周期性非正弦交流量(即上述畸变波形)进行傅里叶级数分解后,所得到的频率大于基波频率整数倍的各次分量,通常称为高次谐波,其中最低次谐波为二次谐波。
电力系统中谐波的产生原因
电力系统中谐波产生的根本原因是非线性负载的存在:当电流流经负载时,若电流与所施加的电压不满足线性关系,则会形成非正弦电流,进而导致电路中产生谐波。
基波与谐波的工程意义
基波是信号或电量中的主要功能成分,而谐波是叠加于基波之上的干扰成分。在波形分析与电力系统运行中,谐波研究具有重要工程意义,因为谐波会带来多方面危害,具体包括:
- 增加设备的铜耗、铁耗与介质损耗,加剧设备的热应力;
- 使电压峰值升高(忽略相位差时,峰值电压上升的标幺值等于电压峰值系数),导致设备绝缘应力增大,可能引发电缆绝缘击穿;
- 导致负载设备损坏(广义定义为“由电压畸变引起的设备故障或工作异常”),缩短设备使用寿命;
- 3 倍数次谐波(如 3 次、6 次、9 次等)即使在三相负载平衡的情况下,也会使中性线产生电流,且该电流可能等于甚至大于相电流,导致零地电位差升高,需对中性线上的开关、电缆等元件进行特殊选型;
- 若谐波引发系统谐振,极大的谐振电流会对电源系统造成严重破坏。
谐波次数
对周期性非正弦电量进行傅里叶级数分解时,除得到与基波频率相同的分量外,还会得到一系列频率大于基波频率的分量,这部分分量统称为谐波。谐波次数的定义为“谐波频率与基波频率的比值”,即:
n
=
f
n
f
1
n = \frac{f_n}{f_1}
n=f1fn
其中,
f
n
f_n
fn 为谐波频率,
f
1
f_1
f1 为基波频率。
通常情况下,谐波频率为基波频率的整数倍。例如,工频为 50 Hz 50\ \text{Hz} 50 Hz 的交流电,其二次谐波频率为 100 Hz 100\ \text{Hz} 100 Hz,三次谐波频率为 150 Hz 150\ \text{Hz} 150 Hz,以此类推,且谐波次数 n n n 的最小值为 2(即不存在频率小于基波频率的谐波)。
音频信号的基波、谐波
逛丢一只鞋 原创已于 2023-03-27 09:40:31 修改
基波与谐波
在振动学理论中,一个振动所产生的波包含一个具有特定频率且振幅最大的正弦波,该正弦波被定义为基波;而所有频率高于基波频率的小波,均称为谐波。
从数学分解角度,谐波是对周期性非正弦交流量进行傅里叶级数分解后,所得到的频率大于基波频率整数倍的各次分量,通常称为高次谐波;基波则特指频率与工频( 50 Hz 50\ \text{Hz} 50 Hz)相同的分量。
电力系统中谐波的产生原因
电力系统中谐波产生的根本原因是非线性负载的存在:当电流流经负载时,若电流与所施加的电压不满足线性关系,则会形成非正弦电流,进而导致电路中产生谐波。
谐波研究的工程意义
谐波研究的意义在于其严重的危害,具体包括:
- 降低电能生产、传输与利用的效率;
- 导致电气设备过热、产生振动与噪声,加速绝缘老化,缩短设备使用寿命,甚至引发设备故障或烧毁;
- 引发电力系统局部并联谐振或串联谐振,导致谐波含量放大,造成电容器等设备烧毁;
- 干扰继电保护与自动装置的正常工作,导致误动作;
- 造成电能计量混乱;
- 对电力系统外部的通信设备与电子设备产生严重干扰。

在复杂的周期性振荡中,其信号成分必然包含基波和谐波。以中国家庭用电( 220 V 220\ \text{V} 220 V、 50 Hz 50\ \text{Hz} 50 Hz)为例, 50 Hz 50\ \text{Hz} 50 Hz 的正弦振荡即为基波;但由于家庭用电场景的复杂性(如大功率家用电器的突然启停),会导致电压幅值降低、电压波形污染,进而产生谐波。
与基波周期对应的频率称为基本频率;频率等于基本频率整数倍的正弦波分量称为谐波。根据傅里叶级数理论,任何周期信号均可分解为以下形式:
a
0
+
a
1
cos
(
ω
0
t
)
+
a
2
cos
(
2
ω
0
t
)
+
⋯
+
b
1
sin
(
ω
0
t
)
+
b
2
sin
(
2
ω
0
t
)
+
⋯
a_0 + a_1\cos(\omega_0 t) + a_2\cos(2\omega_0 t) + \cdots + b_1\sin(\omega_0 t) + b_2\sin(2\omega_0 t) + \cdots
a0+a1cos(ω0t)+a2cos(2ω0t)+⋯+b1sin(ω0t)+b2sin(2ω0t)+⋯
其中:
- a 0 a_0 a0 为直流分量(也称为 0 次谐波);
- 基波(一次谐波):频率为信号的主要频率(基频),在音频信号中,基波是声音的最低频率,决定声音的音调;
- 谐波:频率高于信号的主要频率,例如基频为 50 MHz 50\ \text{MHz} 50 MHz(一次谐波频率)时,谐波频率依次为 100 MHz 100\ \text{MHz} 100 MHz、 150 MHz 150\ \text{MHz} 150 MHz、 ⋯ \cdots ⋯;在音频信号中,谐波的作用是“美化声音、赋予声音色彩”。
音频信号中基波与谐波的均衡调节
对于大多数人声或乐器的音频信号,基波与谐波的均衡调节可遵循以下原则:
- 适当提升基波低端频率的均衡量,可增强声音的温暖感与丰满度;若声音过于沉闷,可衰减基波频率的均衡量;
- 适当提升谐波频率的均衡量,可增强声音的现场感与清晰度;若声音过于刺耳,可衰减谐波频率的均衡量。
常用乐器与人声的基波、谐波参考范围(单位: Hz \text{Hz} Hz)
| 类别 | 基波范围 | 谐波范围 |
|---|---|---|
| 男高音 | 131 − 494 131 - 494 131−494 | 1 k − 12 k 1\ \text{k} - 12\ \text{k} 1 k−12 k |
| 中高音 | 175 − 698 175 - 698 175−698 | 2 k − 12 k 2\ \text{k} - 12\ \text{k} 2 k−12 k |
| 女高音 | 247 − 1175 247 - 1175 247−1175 | 2 k − 12 k 2\ \text{k} - 12\ \text{k} 2 k−12 k |
| 低音人声 | 28 − 4196 28 - 4196 28−4196 | 1 k − 12 k 1\ \text{k} - 12\ \text{k} 1 k−12 k |
| 钢琴 | 28 − 4196 28 - 4196 28−4196 | 5 k − 8 k 5\ \text{k} - 8\ \text{k} 5 k−8 k |
| 电吉他 | 82 − 1319 82 - 1319 82−1319 | 1 k − 15 k 1\ \text{k} - 15\ \text{k} 1 k−15 k |
| 原声吉他 | 82 − 988 82 - 988 82−988 | 1.5 k − 15 k 1.5\ \text{k} - 15\ \text{k} 1.5 k−15 k |
| 电贝司 | 41 − 294 41 - 294 41−294 | 0.7 k − 7 k 0.7\ \text{k} - 7\ \text{k} 0.7 k−7 k |
| 原声贝司 | 41 − 294 41 - 294 41−294 | 0.7 k − 5 k 0.7\ \text{k} - 5\ \text{k} 0.7 k−5 k |
| 大提琴 | 65 − 698 65 - 698 65−698 | 1 k − 6.5 k 1\ \text{k} - 6.5\ \text{k} 1 k−6.5 k |
| 中提琴 | 131 − 1175 131 - 1175 131−1175 | 2 k − 8.5 k 2\ \text{k} - 8.5\ \text{k} 2 k−8.5 k |
| 小提琴 | 196 − 3136 196 - 3136 196−3136 | 4 k − 15 k 4\ \text{k} - 15\ \text{k} 4 k−15 k |
| 底鼓 | 30 − 147 30 - 147 30−147 | 1 k − 6 k 1\ \text{k} - 6\ \text{k} 1 k−6 k |
| 军鼓 | 100 − 200 100 - 200 100−200 | 1 k − 20 k 1\ \text{k} - 20\ \text{k} 1 k−20 k |
| 镲片 | 300 − 587 300 - 587 300−587 | 1 k − 15 k 1\ \text{k} - 15\ \text{k} 1 k−15 k |
| 长笛 | 261 − 2349 261 - 2349 261−2349 | 3 k − 8 k 3\ \text{k} - 8\ \text{k} 3 k−8 k |
| 双簧管 | 261 − 1568 261 - 1568 261−1568 | 2 k − 12 k 2\ \text{k} - 12\ \text{k} 2 k−12 k |
| 单簧管 | 261 − 1568 261 - 1568 261−1568 | 2 k − 10 k 2\ \text{k} - 10\ \text{k} 2 k−10 k |
| 巴松管 | 62 − 587 62 - 587 62−587 | 1 k − 7 k 1\ \text{k} - 7\ \text{k} 1 k−7 k |
| 小号 | 165 − 988 165 - 988 165−988 | 1 k − 7.5 k 1\ \text{k} - 7.5\ \text{k} 1 k−7.5 k |
| 圆号 | 87 − 880 87 - 880 87−880 | 1 k − 6 k 1\ \text{k} - 6\ \text{k} 1 k−6 k |
| 长号 | 73 − 587 73 - 587 73−587 | 1 k − 7.5 k 1\ \text{k} - 7.5\ \text{k} 1 k−7.5 k |
| 大号 | 49 − 587 49 - 587 49−587 | 1 k − 4 k 1\ \text{k} - 4\ \text{k} 1 k−4 k |
谐波次数
频率为基波频率奇数倍的谐波称为奇次谐波(例如基波频率为 50 MHz 50\ \text{MHz} 50 MHz 时, 150 MHz 150\ \text{MHz} 150 MHz、 250 MHz 250\ \text{MHz} 250 MHz 等为奇次谐波)。
对周期性非正弦电量进行傅里叶级数分解时,除得到与基波频率相同的分量外,其余频率大于基波频率的分量统称为谐波。谐波次数的定义为“谐波频率与基波频率的比值”,即:
n
=
f
谐
f
基
n = \frac{f_{\text{谐}}}{f_{\text{基}}}
n=f基f谐
需注意,不存在频率小于基波频率的谐波。
“谐波”一词起源于声学领域,泛音在声学范畴内属于谐波,但二者在次数定义上存在差异:基波频率 2 倍的音频称为一次泛音,基波频率 3 倍的音频称为二次泛音,以此类推。
谐波抑制
为解决电力电子装置及其他谐波源对电网的谐波污染问题,技术思路分为两类:
思路一:装设谐波补偿装置
通过装设谐波补偿装置直接补偿谐波,该方法适用于各类谐波源。传统的谐波补偿装置为 LC 调谐滤波器,其优势在于可同时补偿谐波与无功功率,且结构简单,因此被广泛应用;但缺点是补偿特性受电网阻抗与运行状态影响较大,易与系统发生并联谐振,导致谐波放大,甚至造成 LC 滤波器过载烧毁,且仅能补偿固定频率的谐波,补偿效果有限。
思路二:改造电力电子装置本身
对作为主要谐波源的电力电子装置进行拓扑或控制策略改造,使其运行时不产生谐波,且功率因数可控制为 1。该方法仅适用于电力电子装置类谐波源,但其从根源上消除了谐波产生的可能,是谐波抑制的根本解决方案。
相关概念定义
- 调谐谐波吸收器:由扼流线圈与电容器串联组成的谐振电路,且电路调谐至对特定谐波电流呈现极小阻抗的状态,用于精确清除配电网络中的主要谐波分量。
- 非调谐谐波吸收器:由扼流线圈与电容器串联组成的谐振电路,且电路调谐至低于最低次谐波的频率,以避免与系统发生谐振。
- 谐波电流:由设备或系统引入的非正弦特性电流,该电流叠加于主电源电流之上,导致主电源电流波形畸变。
- 谐波电压:由谐波电流流经配电系统阻抗时产生的电压降,是导致电网电压波形畸变的主要原因之一。
- 阻抗:在特定频率下,配电系统某一点对电流的阻碍作用,其大小取决于变压器、用电设备的参数,以及导体的截面积与长度。
- 阻抗系数:载波频率(AF)下的阻抗与基波频率( 50 Hz 50\ \text{Hz} 50 Hz)下的阻抗的比值。
- 并联谐振频率:配电网络阻抗达到最大值时的频率。在并联谐振电路中,电感支路电流 I L I_L IL 与电容支路电流 I C I_C IC 均大于总电流 I I I。
- 无功功率:用于电动机、变压器等设备建立磁场,或用于功率转换器能量交换的功率,记为 Q Q Q,单位为 Var \text{Var} Var 或 kVar \text{kVar} kVar。与有功功率不同,无功功率不对外做功,但却是电力系统正常运行的必要条件。
- 无功功率补偿:供电部门通常规定最小运行功率因数以避免电能浪费。若工厂的实际功率因数低于该最小值,需额外支付无功功率费用;因此,工厂需通过并联电容器等方式提高功率因数,该过程称为无功功率补偿。
- 谐振:配电系统中的设备与其自身的电容(如电缆、补偿电容器)和电感(如变压器、电抗线圈)构成共振电路,当电路频率与某一次谐波频率一致时,会发生谐振现象。配电系统中谐波的成因之一是变压器铁芯的非线性磁化特性,此时主要产生 3 次谐波,且该谐波在三相导体中长度相同,无法在星形连接的中性点处抵消。
- 谐振频率:每个电感与电容的组合均构成一个具有特定固有频率的谐振电路,一个配电网络中包含多个电感与电容元件时,将对应多个谐振频率。
- 串联谐振电路:由电感(电抗器)与电容(电容器)串联形成的电路,其特征是电路总阻抗随频率变化,在特定频率下呈现纯电阻特性。
- 串联谐振频率:串联谐振电路总阻抗达到最小值时的频率。在串联谐振状态下,电感两端电压 U L U_L UL 与电容两端电压 U C U_C UC 均大于电路总电压 U U U,可能导致元件过电压损坏。
- 分量谐波:频率并非基波频率整数倍的正弦波分量,也称为非整数次谐波,通常由非线性程度较高的负载(如电弧炉、变频器)产生。
信号与系统复习:判断周期性及基波周期的计算
mirevass 原创已于 2024-04-09 22:20:29 修改
前言
在《信号与系统》课程学习中(以奥本海姆教材为参考),信号周期性判断与基波周期计算是基础且关键的知识点。本文将按“连续时间正弦信号”与“离散时间正弦信号”两个维度,分别梳理周期性判断方法与基波周期计算步骤。
在处理周期性相关问题前,首要任务是判断目标正弦信号属于连续时间信号还是离散时间信号——二者的周期性规律存在本质差异,后续分析需分别展开。
一、连续时间正弦信号
(一)单个连续时间正弦信号的周期性
单个连续时间正弦信号的表达式通常为
x
(
t
)
=
A
cos
(
ω
0
t
+
φ
)
x(t) = A\cos(\omega_0 t + \varphi)
x(t)=Acos(ω0t+φ)
其中,
A
A
A 为振幅,
ω
0
\omega_0
ω0 为角频率,
φ
\varphi
φ 为初相位。其本身必然是周期性信号。
(二)基波周期公式
连续时间正弦信号的基波周期
T
T
T(即信号重复一次的最小时间间隔)由角频率
ω
0
\omega_0
ω0 决定,公式为:
T
=
2
π
ω
0
T = \frac{2\pi}{\omega_0}
T=ω02π
其中,
ω
0
\omega_0
ω0 的单位为
rad/s
\text{rad/s}
rad/s,
T
T
T 的单位为
s
\text{s}
s。
(三)多个连续时间正弦信号叠加后的周期性判断
实际问题中常涉及多个连续时间正弦信号的叠加(如 x ( t ) = x 1 ( t ) + x 2 ( t ) x(t) = x_1(t) + x_2(t) x(t)=x1(t)+x2(t)),其周期性需通过以下步骤判断:
- 分步计算单个信号的基波周期:设两个信号的基波周期分别为 T 1 = 2 π ω 1 T_1 = \frac{2\pi}{\omega_1} T1=ω12π、 T 2 = 2 π ω 2 T_2 = \frac{2\pi}{\omega_2} T2=ω22π( ω 1 \omega_1 ω1、 ω 2 \omega_2 ω2 分别为两个信号的角频率);
- 判断周期比的有理数属性:计算周期比 T 1 T 2 \frac{T_1}{T_2} T2T1,若该比值为有理数(即 T 1 T 2 = p q \frac{T_1}{T_2} = \frac{p}{q} T2T1=qp,其中 p p p、 q q q 为互质正整数),则叠加后的信号 x ( t ) x(t) x(t) 为周期性信号;若为无理数,则 x ( t ) x(t) x(t) 为非周期性信号;
- 计算叠加信号的基波周期:若信号为周期性,其基波周期 T T T 为 T 1 T_1 T1 与 T 2 T_2 T2 的最小公倍数(最小公倍数是指能同时被几个数整除的最小正整数),即 T = lcm ( T 1 , T 2 ) T = \text{lcm}(T_1, T_2) T=lcm(T1,T2)。
示例:设 x 1 ( t ) = cos ( 2 t ) x_1(t) = \cos(2t) x1(t)=cos(2t)( T 1 = π T_1 = \pi T1=π)、 x 2 ( t ) = cos ( 4 t ) x_2(t) = \cos(4t) x2(t)=cos(4t)( T 2 = π 2 T_2 = \frac{\pi}{2} T2=2π),周期比 T 1 T 2 = 2 \frac{T_1}{T_2} = 2 T2T1=2(有理数),基波周期 T = lcm ( π , π 2 ) = π T = \text{lcm}(\pi, \frac{\pi}{2}) = \pi T=lcm(π,2π)=π。
二、离散时间正弦信号
离散时间正弦信号的表达式通常为
x
[
n
]
=
A
cos
(
β
0
n
+
φ
)
x[n] = A\cos(\beta_0 n + \varphi)
x[n]=Acos(β0n+φ)
其中,
A
A
A 为振幅,
β
0
\beta_0
β0 为数字角频率,
φ
\varphi
φ 为初相位,
n
n
n 为整数。其周期性判断与连续时间信号存在显著差异。
(一)单个离散时间正弦信号的周期性判断
单个离散时间正弦信号不一定是周期性信号,需通过以下步骤判断:
- 明确数字角频率 β 0 \beta_0 β0: β 0 \beta_0 β0 的单位为 rad \text{rad} rad,是判断周期性的关键参数;
- 计算
2
π
β
0
\frac{2\pi}{\beta_0}
β02π 的属性:
- 若 2 π β 0 \frac{2\pi}{\beta_0} β02π 为整数,则信号 x [ n ] x[n] x[n] 是周期性信号,其基波周期 N = 2 π β 0 N = \frac{2\pi}{\beta_0} N=β02π;
- 若 2 π β 0 \frac{2\pi}{\beta_0} β02π 为有理数(即 2 π β 0 = p q \frac{2\pi}{\beta_0} = \frac{p}{q} β02π=qp,其中 p p p、 q q q 为互质正整数),则需引入最小整数 m = q m = q m=q,使 N = m ⋅ 2 π β 0 = p N = m \cdot \frac{2\pi}{\beta_0} = p N=m⋅β02π=p(整数),此时基波周期 N = p N = p N=p;
- 若 2 π β 0 \frac{2\pi}{\beta_0} β02π 为无理数,则信号 x [ n ] x[n] x[n] 为非周期性信号,不存在基波周期。
示例:
- 设 x [ n ] = cos ( π 8 n ) x[n] = \cos(\frac{\pi}{8}n) x[n]=cos(8πn), 2 π β 0 = 2 π π / 8 = 16 \frac{2\pi}{\beta_0} = \frac{2\pi}{\pi/8} = 16 β02π=π/82π=16(整数),故基波周期 N = 16 N = 16 N=16;
- 若 x [ n ] = cos ( 2 π 3 n ) x[n] = \cos(\frac{2\pi}{3}n) x[n]=cos(32πn), 2 π β 0 = 3 \frac{2\pi}{\beta_0} = 3 β02π=3(整数),基波周期 N = 3 N = 3 N=3;
- 若 x [ n ] = cos ( π 7 n ) x[n] = \cos(\frac{\pi}{7}n) x[n]=cos(7πn), 2 π β 0 = 14 \frac{2\pi}{\beta_0} = 14 β02π=14(整数),基波周期 N = 14 N = 14 N=14。
(二)多个离散时间正弦信号叠加后的周期性判断
若组成叠加信号的每个离散时间正弦信号均为周期性序列,则叠加后的信号必然是周期性序列。其基波周期计算规则为:叠加信号的基波周期 N N N 为各组成序列基波周期 N 1 , N 2 , … , N k N_1, N_2, \dots, N_k N1,N2,…,Nk 的最小公倍数,即 N = lcm ( N 1 , N 2 , … , N k ) N = \text{lcm}(N_1, N_2, \dots, N_k) N=lcm(N1,N2,…,Nk)。
示例:设 x 1 [ n ] = cos ( π 4 n ) x_1[n] = \cos(\frac{\pi}{4}n) x1[n]=cos(4πn)(基波周期 N 1 = 8 N_1 = 8 N1=8)、 x 2 [ n ] = cos ( π 6 n ) x_2[n] = \cos(\frac{\pi}{6}n) x2[n]=cos(6πn)(基波周期 N 2 = 12 N_2 = 12 N2=12),则叠加信号的基波周期 N = lcm ( 8 , 12 ) = 24 N = \text{lcm}(8, 12) = 24 N=lcm(8,12)=24。
三、注意要点
-
非标准形式信号的预处理:若遇到 x [ n ] = cos 2 ( π 8 n ) x[n] = \cos^2(\frac{\pi}{8}n) x[n]=cos2(8πn) 等非标准形式的信号(与标准模型 x ( t ) = A cos ( ω 0 t + φ ) x(t) = A\cos(\omega_0 t + \varphi) x(t)=Acos(ω0t+φ) 或 x [ n ] = A cos ( β 0 n + φ ) x[n] = A\cos(\beta_0 n + \varphi) x[n]=Acos(β0n+φ) 不符),需先通过三角恒等变换将其转化为标准形式,再进行周期性判断。例如:
cos 2 ( π 8 n ) = 1 2 + 1 2 cos ( π 4 n ) \cos^2(\frac{\pi}{8}n) = \frac{1}{2} + \frac{1}{2}\cos(\frac{\pi}{4}n) cos2(8πn)=21+21cos(4πn)
转化后可判断 cos ( π 4 n ) \cos(\frac{\pi}{4}n) cos(4πn) 的基波周期为 8 8 8,因此 x [ n ] x[n] x[n] 为周期性信号,基波周期 N = 8 N = 8 N=8。 -
连续与离散信号的差异:
- 单个连续时间正弦信号一定是周期性信号;单个离散时间正弦信号不一定是周期性信号,需依赖 2 π β 0 \frac{2\pi}{\beta_0} β02π 的有理数属性判断。
- 多个连续时间正弦信号叠加后,仅当周期比为有理数时才是周期性信号;多个离散时间周期序列叠加后,必然是周期性信号。
-
离散信号基波周期的计算边界:若 2 π β 0 \frac{2\pi}{\beta_0} β02π 为无理数,离散信号无周期性,此时无需强行计算基波周期,避免无效推导。
射频领域中杂散与谐波
在射频(RF)领域中,杂散(Spurious)和谐波(Harmonic)是两类典型的非期望信号,二者在定义边界、产生机制、信号特性及工程应对方式上存在明确差异,准确区分二者是射频系统设计、调试与性能优化的前提之一。
1. 边界清晰的两类非期望信号
1.1 谐波(Harmonic)
谐波是与基波存在“整数倍频率关联”的非期望信号分量,其频率严格遵循“ n f 0 nf_0 nf0 ”规律(其中 f 0 f_0 f0 为基波频率, n n n 为大于 1 的正整数,即 n = 2 , 3 , 4 … n=2,3,4\ldots n=2,3,4… ),且本质上是基波经非线性变换后“衍生”的信号。
例如:若基波为 1GHz(常见于射频通信、测试仪器),其二次谐波为 2GHz、三次谐波为 3GHz、四次谐波为 4GHz,频率与基波的整数倍关系具有确定性。
1.2 杂散(Spurious)
杂散是排除基波及其谐波后,所有额外出现的非期望信号总称,其频率与基波无“整数倍”关联,可出现在射频频段内的任意频率点,信号来源既可能是系统内部生成,也可能是外部环境引入。
例如:某 1GHz 基波信号的射频系统中,若出现 1.5GHz、2.8GHz 等与 1GHz 无整数倍关系的信号,或外部环境耦合的 2.4GHz Wi-Fi 干扰信号,均属于杂散范畴。
2. 产生原因
非线性是共性,但来源范围不同。
2.1 谐波
仅由“内部非线性元件”主导产生。
谐波的产生机制高度单一,是射频系统内部非线性元件的“信号失真”效应,具体场景包括:
- 放大器(如功率放大器 PA、低噪声放大器 LNA):若工作点偏离线性区(如 PA 为追求高输出功率进入饱和区),会对输入基波信号产生“幅度压缩”,进而生成谐波;
- 混频器:作为频率转换器件,其内部二极管/晶体管的非线性特性会导致基波与本振信号混合时,额外产生谐波分量;
- 其他非线性器件:如调制器、倍频器、非线性电阻等,在信号处理过程中均可能因非线性变换生成谐波。
2.2 杂散
内部缺陷与外部干扰的“综合产物”。
杂散的产生原因具有多样性,涵盖“内部非线性”“外部干扰”“设计缺陷”三大类,具体包括:
- 内部非线性衍生:与谐波同源(如放大器、混频器的非线性),但频率不满足整数倍关系的信号(如互调产物,即两个不同频率信号 f 1 、 f 2 f_1、f_2 f1、f2 经非线性变换生成的 m f 1 ± n f 2 mf_1\pm nf_2 mf1±nf2 信号,若 m 、 n m、n m、n 为非 1 整数且不满足谐波规律,即属于杂散);
- 外部电磁干扰(EMI):外部设备(如雷达、微波炉、其他射频发射机)的辐射信号通过空间耦合或线缆传导进入系统,形成杂散;
- 电源干扰:电源模块(如 DC-DC 转换器)的纹波、噪声(如开关噪声)通过电源走线耦合到射频链路,生成杂散;
- 电路设计缺陷:如滤波器阻带抑制不足(未能滤除外部干扰)、射频走线与数字走线交叉耦合、接地不良导致的信号串扰等,均会引入杂散。
3. 特性
频率与幅度的规律性差异显著。
3.1 谐波
谐波的特性是“频率与幅度均有明确规律”:频率确定,幅度递减。
- 频率规律:严格为基波的整数倍( 2 f 0 、 3 f 0 … 2f_0、3f_0\ldots 2f0、3f0… ),可通过基波频率直接计算得出;
- 幅度规律:通常随谐波次数 n n n 的增加而单调递减(因非线性元件对高次谐波的“生成能力”减弱),例如二次谐波幅度通常为基波的-20dB-40dB,三次谐波幅度更低(-40dB-60dB);
- 数学描述:可通过傅里叶级数展开精确描述(基波与各次谐波的叠加构成失真后的信号),工程中可通过理论计算预估谐波幅度。
3.2 杂散
杂散的特性是“频率与幅度均无固定规律”:频率随机,幅度无规律。
- 频率分布:无固定范围,可出现在基波频段内、谐波频段之间或远离基波的频段(如 1GHz 基波系统中,杂散可能出现在 1.2GHz、2.5GHz 等任意频率);
- 幅度特性:幅度大小与频率无关联,可能远低于谐波(如-80dBm 以下的微弱干扰),也可能因外部强干扰而高于谐波(如近场环境中 2.4GHz Wi-Fi 信号耦合进入系统,幅度可达-30dBm);
- 数学描述:难以通过简单模型预估,需结合实际场景(如系统布局、外部环境)通过频谱测量确定。
4. 测试与测量
方法因“规律性”差异而不同。
两类信号的测量均以频谱分析仪(SA) 为工具,但因特性差异,测试参数设置与流程存在明显区别:
| 测量维度 | 谐波(Harmonic) | 杂散(Spurious) |
|---|---|---|
| 频率扫描范围 | 窄范围(仅需覆盖基波+预期高次谐波,如 1GHz 基波仅需扫描 1~5GHz) | 宽范围(需覆盖系统工作频段及可能的干扰频段,如 1GHz 系统需扫描 100MHz~10GHz) |
| 分辨率带宽(RBW) | 固定窄带宽(匹配谐波信号带宽,避免相邻谐波混叠) | 动态调整(对微弱杂散用窄 RBW 提高灵敏度,对宽频干扰用宽 RBW 加快扫描速度) |
| 关键操作 | 无需屏蔽(谐波为内部生成,外部干扰影响小) | 需屏蔽(使用屏蔽箱/暗室,排除外部干扰对杂散测量的影响) |
| 结果判断 | 对比“实测频率与 n f 0 nf_0 nf0 ”是否一致,验证谐波次数 | 排除基波与谐波后,所有额外信号均判定为杂散 |
5. 影响与抑制
针对性措施需匹配产生机制。
5.1 谐波的影响与抑制
影响
- 信号失真:谐波叠加会导致基波信号波形失真(如正弦波变为方波),降低信号纯净度;
- 邻频干扰:若谐波频率落入其他系统的工作频段,会造成干扰(如 4G LTE 基站的 2.1GHz 基波,其二次谐波 4.2GHz 可能干扰 5G NR 的 4.9GHz 频段)。
抑制措施
- 优化器件工作点:将放大器、混频器等非线性器件调整至线性工作区(如 PA 采用“回退功率”方式,牺牲部分输出功率以降低非线性);
- 增加滤波电路:在射频链路中串联低通滤波器(LPF,滤除高次谐波)或带阻滤波器(BRF,针对性抑制特定次数谐波);
- 采用线性化技术:如功率放大器的预失真(DPD)技术,通过提前补偿非线性失真,减少谐波生成。
5.2 杂散的影响与抑制
影响
- 噪声底抬升:微弱杂散会提高系统噪声底,降低接收机对有用信号的灵敏度;
- 误判/误码:在雷达、通信系统中,杂散可能被误识别为有用信号(如雷达误判杂散为目标回波),或导致数字通信误码率升高。
抑制措施
- 电源优化:采用低纹波电源模块,在电源入口处增加滤波电容(如陶瓷电容+电解电容组合),抑制电源噪声耦合;
- 电磁屏蔽:对射频链路(如 PCB 走线、连接器)采用金属屏蔽罩,减少外部 EMI 入侵;对外部干扰源(如数字电路)进行屏蔽,避免干扰射频部分;
- 布局布线优化:射频走线短而直,避免与数字走线、电源走线平行;数字地与射频地单点连接,减少地环路串扰;优化滤波器设计(如提高阻带抑制比),滤除特定频段杂散。
6. 应用案例
6.1 谐波案例:Wi-Fi 发射机的邻频干扰
某工作在 2.4GHz 频段的 Wi-Fi 5(802.11ac)发射机,其功率放大器为追求覆盖范围,工作点偏近饱和区,生成二次谐波(4.8GHz)。由于 4.8GHz 靠近 5GHz Wi-Fi 频段(5.15~5.85GHz),若该谐波幅度超过 regulatory 标准(如 FCC 规定的-40dBm/MHz),会干扰 5GHz Wi-Fi 设备的正常通信,导致其吞吐量下降。
6.2 杂散案例:雷达系统的目标误判
某船用导航雷达(工作频率 9.3GHz),其电源模块的开关噪声(100kHz~1MHz)通过电源走线耦合到发射链路,生成 10.1GHz 的杂散信号。当雷达接收目标回波时,该 10.1GHz 杂散信号与目标回波(9.3GHz 附近)一同被接收机接收,若杂散幅度超过检测阈值,会被误判为“近距离小目标”,导致雷达显示虚假目标,影响导航安全。
总结
谐波与杂散虽同属射频系统中的非期望信号,但二者的差异可概括为“规律性 vs 随机性”:
- 谐波是“有规律的内部衍生信号”:频率为基波整数倍,由内部非线性元件生成,幅度随次数递减,可通过理论计算与针对性滤波抑制;
- 杂散是“无规律的综合干扰信号”:频率与基波无关联,来源涵盖内部缺陷与外部干扰,幅度无规律,需通过宽频测量、屏蔽与系统优化抑制。
在射频工程实践中,准确区分二者的性质与来源,是制定有效抑制方案、保障系统性能(如通信信噪比、雷达探测精度)的关键前提。
via:
-
基波、载波、谐波-优快云博客
https://blog.youkuaiyun.com/Kevin_Z_Q/article/details/120953094 -
理解基波与谐波:概念、影响与分析-优快云博客
https://blog.youkuaiyun.com/qq_53145551/article/details/131490936 -
电力系统中的谐波现象与谐波抑制技术-优快云博客
https://blog.youkuaiyun.com/szm1234/article/details/121053397 -
【信号与系统-复习】判断周期性及基波周期的计算_基波周期怎么求-优快云博客
https://blog.youkuaiyun.com/Aliothxx/article/details/135361713 -
……





















 1485
1485

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








