虚数 | 定义 / 存在性 / 可视化理解

注：本文为 “虚数” 相关合辑。
英文引文，机翻未校。
中文引文，为 阮一峰《虚数的意义》 重排版。
如有内容异常，请看原文。

---

图解虚数 $i$ 的意义

作者：阮一峰 发表日期：2012 年 9 月 24 日

在 Stack Exchange 平台上，有用户提出如下问题：

“我始终认为虚数（imaginary number）难以理解。
中学阶段，教师提及虚数即 $-1$ 的平方根，表达式为
 
$i=\sqrt{-1}$
 
然而，不存在任何实数的平方等于 $-1$ ，计算器对此操作也会直接显示错误。
直至今日，我仍未理解虚数的本质。恳请解释虚数究竟是什么？
它具有哪些实际用途？”

该问题下方有众多用户参与解答，同时有用户推荐了一篇阐释虚数的优质文章：

• A Visual, Intuitive Guide to Imaginary Numbers – BetterExplained
  https://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/

笔者读后深受启发，得以清晰理解虚数的本质，其概念并非复杂难懂。下文将以笔者的理解，系统阐述虚数的相关概念。

一、虚数的定义

首先，构建一根数轴，轴上存在两个方向相反的点，分别对应 $+1$ 与 $-1$ 。

该数轴的正向部分可绕原点旋转。显然，当 $+1$ 绕原点逆时针旋转 $180^{\circ }$ 后，其位置将与 $-1$ 重合。

这一旋转过程等效于 $+1$ 绕原点连续两次逆时针旋转 $90^{\circ }$ 。

基于上述等效关系，可推导得出如下关系式：

$(+1)\times (\text{逆时针旋转}90^{\circ })\times (\text{逆时针旋转}90^{\circ })=-1$

若将式中的 $+1$ 消去，关系式简化为：

$(\text{逆时针旋转}90^{\circ }{)}^2=-1$

将“逆时针旋转 $90^{\circ }$ ”这一操作定义为 $i$ ，则有：

$i^2=-1$

该式与虚数的定义式完全一致。

由此可得出结论：

虚数 $i$ 的本质是“逆时针旋转 $90^{\circ }$ ”的操作，并非传统意义上的数，而是一个表示旋转量的符号。

二、复数的定义

由于 $i$ 表示旋转量，因此可借助 $i$ 描述任意实数的旋转状态。

若将实数轴作为平面直角坐标系的横轴，虚数轴作为纵轴，可构成一个二维平面（即复平面）。

此时，旋转至某一角度的任意正实数，均唯一对应复平面内的某个点。

确定复平面内某点的位置，需明确其横坐标与纵坐标。例如，坐标 $(1,i)$ 对应旋转量为 $45^{\circ }$ 的实数。

数学家采用特定形式表示复平面内的二维坐标：通过“ $+$ ”号连接横坐标与纵坐标。以坐标 $(1,i)$ 为例，其对应表示形式为“ $1+i$ ”。

此类由实数部分与虚数部分组成的表达式称为复数（complex number），其中 $1$ 为实数部， $i$ 为虚数部。

将二维坐标采用此形式表示的原因，将在后续章节中阐述。

三、虚数的加法运算

虚数的引入，显著简化了涉及旋转的计算过程。

以物理学中的“力的合成”问题为例：假设存在两个力，分别表示为 $3+i$ 与 $1+3i$ ，需计算这两个力的合成力大小及方向。

根据力学中的“平行四边形法则”，可直接通过复数加法计算合成力：

$(3+i)+(1+3i)=4+4i$

上述计算过程直观体现了虚数加法的物理意义：用于合成具有旋转属性的物理量（如力、速度等）。

四、虚数的乘法运算

在需要改变旋转角度的场景中，虚数乘法的优势更为突出。

以船舶航向调整为例：假设某船舶的初始航向表示为 $3+4i$ ，若需将航向逆时针偏转 $45^{\circ }$ ，求调整后的新航向。

在复平面中， $45^{\circ }$ 对应的复数为 $1+i$ 。此时，新航向可通过初始航向与 $45^{\circ }$ 对应复数的乘法运算求得（运算原理将在第五节证明）：

$(3+4i)\times (1+i)=-1+7i$

因此，该船舶调整后的新航向为 $-1+7i$ 。

若需将航向逆时针偏转 $90^{\circ }$ ，计算过程更为简便。由于 $90^{\circ }$ 对应的复数为 $i$ ，新航向的表达式为：

$(3+4i)\times i=-4+3i$

上述案例清晰表明虚数乘法的物理意义：用于改变具有旋转属性的物理量的角度（如航向、相位等）。

五、虚数乘法的数学证明

为何通过复数乘法可实现旋转角度的改变？以下将从数学角度进行严谨证明。

对于任意复数 $a+bi$ ，均可将其表示为“旋转半径 $r$ 与横轴夹角 $\theta$ ”的形式（即极坐标形式）。

假设存在两个复数 $a+bi$ 与 $c+di$ ，将其分别转化为极坐标形式：

$a+bi=r_1\times (\cos \alpha +i\sin \alpha )$
$c+di=r_2\times (\cos \beta +i\sin \beta )$

其中， $r_1$ 、 $r_2$ 分别为两个复数的旋转半径， $\alpha$ 、 $\beta$ 分别为两个复数与横轴的夹角。

计算两个复数的乘积 $(a+bi)(c+di)$ ，代入极坐标形式可得：

$r_1\times r_2\times (\cos \alpha +i\sin \alpha )\times (\cos \beta +i\sin \beta )$

对上述表达式中的三角函数部分展开：

$\cos \alpha \times \cos \beta -\sin \alpha \times \sin \beta +i(\cos \alpha \times \sin \beta +\sin \alpha \times \cos \beta )$

根据三角函数的和角公式：

• $\cos (\alpha +\beta )=\cos \alpha \times \cos \beta -\sin \alpha \times \sin \beta$
• $\sin (\alpha +\beta )=\cos \alpha \times \sin \beta +\sin \alpha \times \cos \beta$

可将展开式简化为：

$\cos (\alpha +\beta )+i\sin (\alpha +\beta )$

因此，两个复数的乘积最终表示为：

$(a+bi)(c+di)=r_1\times r_2\times [\cos (\alpha +\beta )+i\sin (\alpha +\beta )]$

综上，数学证明可得出结论：

两个复数相乘，其结果的旋转半径为两个复数旋转半径的乘积，其结果的旋转角度为两个复数旋转角度的和。

---

What are imaginary numbers?

什么是虚数？

At school, I really struggled to understand the concept of imaginary numbers. My teacher told us that an imaginary number is a number that has something to do with the square root of $-1$. When I tried to calculate the square root of $-1$ on my calculator, it gave me an error. To this day I still do not understand imaginary numbers. It makes no sense to me at all. Is there someone here who totally gets it and can explain it?
上学时，我一直很难理解虚数的概念。老师告诉我们，虚数是一种与 $\sqrt{-1}$ 有关的数。可当我试着在计算器上计算 $\sqrt{-1}$ 时，却得到了错误提示。直到现在，我还是没弄懂虚数，它对我来说完全没有意义。有没有完全理解虚数的人能帮忙解释一下？

Why is the concept even useful?
这个概念到底有什么用呢？

edited Dec 29, 2019 at 19:48
Simon Fraser
asked Sep 20, 2012 at 12:18
Sachin Kainth

I don’t get it.
我还是没懂。

– Sachin Kainth
Commented Sep 20, 2012 at 12:28

@SachinKainth: What is a real number? I mean, what do you understand a real number to be and why do you not struggle with that concept? If people see that you understand such numbers for particular reasons, they may be able to give similar reasons for the existence of complex numbers, or at least gauge what would be required to convince you that complex numbers are useful.
@萨钦・凯恩思：什么是实数？我是说，你认为实数是什么，为什么你理解实数概念没有困难？如果大家知道你理解这类数的具体原因，或许能给出类似的理由来解释复数的存在，至少能判断需要用什么方式才能让你相信复数是有用的。

– Michael Albanese
Commented Sep 20, 2012 at 12:54

ReallyReally exist?
它们真的存在吗？

– user1729
Commented Sep 20, 2012 at 13:14

Real numbers don’t “exist” either, they’re all just mathematicians’ ideas.
实数也不是 “真实存在” 的，它们都只是数学家提出的概念而已。

– akkkk
Commented Sep 20, 2012 at 13:30

@ivan Your comment is misleading. A complex number is a number on the plane. An imaginary number is merely the second coordinate in 2D, the imaginary part of the complex number.
@伊万 你的评论有误导性。复数是平面上的数，而虚数只是二维平面中的第二个坐标，即复数的虚部。

– Rudy the Reindeer
Commented Sep 20, 2012 at 15:56

Answers

Let’s go through some questions in order and see where it takes us. [Or skip to the bit about complex numbers below if you can’t be bothered.]
我们按顺序探讨几个问题，看看能得出什么结论。（如果没耐心，也可以直接跳到下面关于复数的部分。）

What are natural numbers?

什么是自然数？

It took quite some evolution, but humans are blessed by their ability to notice that there is a similarity between the situations of having three apples in your hand and having three eggs in your hand. Or, indeed, three twigs or three babies or three spots. Or even three knocks at the door. And we generalise all of these situations by calling it ‘three’; same goes for the other natural numbers. This is not the construction we usually take in maths, but it’s how we learn what numbers are.
人类经过漫长的发展，拥有了一种特殊能力：能发现 “手里有 3 个苹果” 和 “手里有 3 个鸡蛋” 这两种场景的共性 —— 同样是 “3 个”。类似地，3 根树枝、3 个婴儿、3 个斑点，甚至 3 声敲门声，我们都能将这些场景归纳为 “3”；其他自然数的概念也是这样形成的。这并非数学中定义自然数的标准方式，但却是我们学习数字概念的最初途径。

Natural numbers are what allow us to count a finite collection of things. We call this set of numbers $\mathbb{N}$.
自然数是用来计数有限集合中事物数量的数，我们将这个数集记为 $\mathbb{N}$。

What are integers?

什么是整数？

Once we’ve learnt how to measure quantity, it doesn’t take us long before we need to measure change, or relative quantity. If I’m holding three apples and you take away two, I now have ‘two fewer’ apples than I had before; but if you gave me two apples I’d have ‘two more’. We want to measure these changes on the same scale (rather than the separate scales of ‘more’ and ‘less’), and we do this by introducing negative natural numbers: the net increase in apples is $-2$.
一旦我们学会了计量 “数量”，很快就会需要计量 “变化量” 或 “相对数量”。比如我手里有 3 个苹果，你拿走 2 个，我就比之前 “少了 2 个” 苹果；但如果你给我 2 个苹果，我就比之前 “多了 2 个”。我们希望用统一的尺度来计量这种 “多” 和 “少” 的变化（而非用两个独立的尺度），于是引入了负自然数：此时苹果的净增量为 $-2$。

We get the integers from the naturals by allowing ourselves to take numbers away: $\mathbb{Z}$ is the closure of $\mathbb{N}$ under the operation $-$.
整数是在自然数的基础上，通过允许 “减法运算” 得到的：$\mathbb{Z}$ 是 $\mathbb{N}$ 在 $-$ 运算下的闭包。

What are rational numbers?

什么是有理数？

My friend and I are pretty hungry at this point but since you came along and stole two of my apples I only have one left. Out of mutual respect we decide we should each have the same quantity of apple, and so we cut it down the middle. We call the quantity of apple we each get ‘a half’, or $\frac{1}{2}$. The net change in apple after I give my friend his half is $-\frac{1}{2}$.
这时我和朋友都很饿，但因为你拿走了我的 2 个苹果，我只剩 1 个苹果了。出于互相尊重，我们决定平分这个苹果，于是把它切成两半。我们把每人得到的苹果量称为 “二分之一”，即 $\frac{1}{2}$。我给朋友一半苹果后，苹果的净变化量为 $-\frac{1}{2}$。

We get the rationals from the integers by allowing ourselves to divide integers by positive integers [or, equivalently, by nonzero integers]: $\mathbb{Q}$ is (sort of) the closure of $\mathbb{Z}$ under the operation $÷$.
有理数是在整数的基础上，通过允许 “整数除以正整数（或等价地，除以非零整数）” 得到的：$\mathbb{Q}$（大致上）是 $\mathbb{Z}$ 在 $÷$ 运算下的闭包。

What are real numbers?

什么是实数？

I find some more apples and put them in a pie, which I cook in a circular dish. One of my friends decides to get smart, and asks for a slice of the pie whose curved edge has the same length as its straight edges (i.e. arc length of the circular segment is equal to its radius). I decide to honour his request, and using our newfangled rational numbers I try to work out how many such slices I could cut. But I can’t quite get there: it’s somewhere between $6$ and $7$; somewhere between $\frac{43}{7}$ and $\frac{44}{7}$; somewhere between $\frac{709}{113}$ and $\frac{710}{113}$; and so on, but no matter how accurate I try and make the fractions, I never quite get there. So I decide to call this number $2\pi$ (or $\tau$?) and move on with my life.
我又找了些苹果，做成派放进圆形烤盘里烘烤。有个朋友想考考我，想要一块 “曲边长度和直边长度相等” 的派（即圆弧段的弧长等于半径）。我决定满足他的要求，并用我们新学的有理数尝试计算能切出多少块这样的派。但我始终无法得到精确值：这个数量介于 $6$ 和 $7$ 之间，介于 $\frac{43}{7}$ 和 $\frac{44}{7}$ 之间，还介于 $\frac{709}{113}$ 和 $\frac{710}{113}$ 之间…… 无论我把分数精度提得多高，都无法精确表示它。于是我决定把这个数称为 $2\pi$（或者 $\tau$？），然后继续做其他事。

The reals turn the rationals into a continuum, filling the holes which can be approximated to arbitrary degrees of accuracy but never actually reached: $\mathbb{R}$ is the completion of $\mathbb{Q}$.
实数将有理数扩展为连续统，填补了那些 “能被任意精度逼近但永远无法精确达到” 的空隙：$\mathbb{R}$ 是 $\mathbb{Q}$ 的完备化。

What are complex numbers? [Finally!]

什么是复数？（终于到了！）

Our real numbers prove to be quite useful. If I want to make a pie which is twice as big as my last one but still circular then I’ll use a dish whose radius is $\sqrt{2}$ times bigger. If I decide this isn’t enough and I want to make it thrice as big again then I’ll use a dish whose radius is $\sqrt{3}$ times as big as the last. But it turns out that to get this dish I could have made the original one thrice as big and then that one twice as big; the order in which I increase the size of the dish has no effect on what I end up with. And I could have done it in one go, making it six times as big by using a dish whose radius is $\sqrt{6}$ times as big. This leads to my discovery of the fact that multiplication corresponds to scaling — they obey the same rules. (Multiplication by negative numbers responds to scaling and then flipping.)
实数确实很有用。比如我想做一个比上次大两倍的圆形派，就需要用半径为原来 $\sqrt{2}$ 倍的烤盘。如果觉得还不够大，想再扩大三倍，就用半径为上次 $\sqrt{3}$ 倍的烤盘。但我发现，要得到最终的烤盘，也可以先把原始烤盘扩大三倍，再扩大两倍 —— 扩大顺序不影响最终结果。而且我还可以一步到位：用半径为原始 $\sqrt{6}$ 倍的烤盘，直接做出六倍大的派。这让我发现了一个规律：乘法对应 “缩放”—— 两者遵循相同的规则（乘以负数则对应 “缩放后再翻转”）。

But I can also spin a pie around. Rotating it by one angle and then another has the same effect as rotating it by the second angle and then the first — the order in which I carry out the rotations has no effect on what I end up with, just like with scaling. Does this mean we can model rotation with some kind of multiplication, where multiplication of these new numbers corresponds to addition of the angles? If I could, then I’d be able to rotate a point on the pie by performing a sequence of multiplications. I notice that if I rotate my pie by $90^{\circ }$ four times then it ends up how it was, so I’ll declare this $90^{\circ }$ rotation to be multiplication by $i$ and see what happens. We’ve seen that $i^4=1$, and with our funky real numbers we know that $i^4=(i^2{)}^2$ and so $i^2=\pm 1$. But $i^2\ne 1$ since rotating twice doesn’t leave the pie how it was — it’s facing the wrong way; so in fact $i^2=-1$. This then also obeys the rules for multiplication by negative real numbers.
但派还可以旋转。先转一个角度再转另一个角度，和先转第二个角度再转第一个角度的结果相同 —— 旋转顺序不影响最终状态，这和缩放很像。这是否意味着我们可以用某种乘法来模拟旋转，让新数字的乘法对应角度的加法？如果可以，那我就能通过一系列乘法来旋转派上的点。我发现，把派旋转 $90^{\circ }$ 四次后，它会回到初始状态，于是我定义 “旋转 $90^{\circ }$” 相当于 “乘以 $i$”，看看会发生什么。我们知道 $i^4=1$，结合实数的运算规则，又能得出 $i^4=(i^2{)}^2$，因此 $i^2=\pm 1$。但旋转两次（即乘以 $i^2$）并不会让派回到初始状态 —— 它会朝向相反方向，所以 $i^2\ne 1$，实际上 $i^2=-1$。这个定义也符合负实数的乘法规则。

Upon further experimentation with spinning pies around we discover that defining $i$ in this way leads to numbers (formed by adding and multiplying real numbers with this new $i$ beast) which, under multiplication, do indeed correspond to combined scalings and rotations in a ‘number plane’, which contains our previously held ‘number line’. What’s more, they can be multiplied, divided and rooted as we please. It then has the fun consequence that any polynomial with coefficients of this kind has as many roots as its degree; what fun!
通过进一步旋转派的实验，我们发现：用这种方式定义 $i$ 后，由 “实数与 $i$ 进行加减乘运算” 形成的新数字，其乘法运算确实对应 “数字平面” 中的 “缩放 + 旋转” 组合（这个数字平面包含了我们之前熟悉的 “数轴”）。更重要的是，这些新数字可以自由地进行乘、除、开方运算，还带来了一个有趣的结果：任何以这种数字为系数的多项式，其根的个数恰好等于它的次数 —— 多有意思啊！

The complex numbers allow us to consider scalings and rotations as two instances of the same thing; and by ensuring that negative reals have square roots, we get something where every (non-constant) polynomial equation can be solved: $\mathbb{C}$ is the algebraic closure of $\mathbb{R}$.
复数能将 “缩放” 和 “旋转” 统一为同一种运算的两种表现；同时，它让负实数也有了平方根，并且使得 “所有（非常数）多项式方程都能求解”：$\mathbb{C}$ 是 $\mathbb{R}$ 的代数闭包。

[Final edit ever: It occurs to me that I never mentioned anything to do with anything ‘imaginary’, since I presumed that Sachin really wanted to know about the complex numbers as a whole. But for the sake of completeness: the imaginary numbers are precisely the real multiples of $i$ — you scale the pie and rotate it by $90^{\circ }$ in either direction. They are the rotations/scalings which, when performed twice, leave the pie facing backwards; that is, they are the numbers which square to give negative real numbers.]
[* 最终修改 ：我意识到之前没提过 “虚数” 相关内容，因为我默认萨钦真正想了解的是整个 “复数” 体系。但为了完整起见，还是补充一下：* 虚数 ** 正是 $i$ 的实数倍数 —— 即 “缩放派的同时，向任意方向旋转 $90^{\circ }$” 对应的数。这类旋转 / 缩放操作连续进行两次后，派会朝向相反方向；也就是说，虚数的平方是负实数。]

What next?

接下来是什么？

I’ve been asked in the comments to mention quaternions and octonions. These go (even further) beyond what the question is asking, so I won’t dwell on them, but the idea is: my friends and I are actually aliens from a multi-dimensional world and simply aren’t satisfied with a measly $2$-dimensional number system. By extending the principles from our so-called complex numbers we get systems which include copies of $\mathbb{C}$ and act in many ways like numbers, but now (unless we restrict ourselves to one of the copies of $\mathbb{C}$) the order in which we carry out our weird multi-dimensional symmetries does matter. But, with them, we can do lots of science.
有评论要求我提一下四元数和八元数。它们超出了本题的范围，所以我不展开讲，但核心思路是：假设我和朋友是来自多维世界的外星人，对只有 $2$ 维的复数系不满意。通过扩展复数的定义原则，我们能得到包含 $\mathbb{C}$ 副本的新数系，它们在很多方面都像 “数”，但此时（除非限制在某个 $\mathbb{C}$ 副本内），多维对称操作的顺序会影响结果。不过，这些数系在科学研究中有着广泛用途。

I have also completely omitted any mention of ordinal numbers, because they fork off in a different direction straight after the naturals. We get some very exciting stuff out of these, but we don’t find $\mathbb{C}$ because it doesn’t have any natural order relation on it.
我还完全没提序数，因为它从自然数出发就走向了另一个方向。序数能衍生出很多有趣的理论，但它和 $\mathbb{C}$ 无关，因为复数系不存在自然的序关系。

Historical note

历史说明

The above succession of stages is not a historical account of how numbers of different types are discovered. I don’t claim to know an awful lot about the history of mathematics, but I know enough to know that the concept of a number evolved in different ways in different cultures, likely due to practical implications. In particular, it is very unlikely that complex numbers were devised geometrically as rotations-and-scalings — the needs of the time were algebraic and people were throwing away (perfectly valid) equations because they didn’t think $\sqrt{-1}$ could exist. Their geometric properties were discovered soon after.
以上数系的演进过程，并非不同类型数字的实际发现史。我对数学史了解不多，但也知道 “数” 的概念在不同文化中以不同方式演变，且很可能源于实际需求。尤其是复数，它不太可能是通过 “旋转 + 缩放” 的几何方式发明的 —— 当时的需求是 “代数层面” 的：人们因为不相信 $\sqrt{-1}$ 存在，而丢弃了一些（完全有效的）方程。复数的几何性质是在之后才被发现的。

However, this is roughly the sequence in which these number sets are (usually) constructed in ZF set theory and we have a nice sequence of inclusions
不过，这大致是 ZF 集合论中（通常）构造这些数集的顺序，且它们满足以下包含关系：

$1\hookrightarrow \mathbb{N}\hookrightarrow \mathbb{Z}\hookrightarrow \mathbb{Q}\hookrightarrow \mathbb{R}\hookrightarrow \mathbb{C}$

Stuff to read

推荐阅读

• The other answers to this question give very insightful ways of getting $\mathbb{C}$ from $\mathbb{R}$ in different ways, and discussing how and why complex numbers are useful — there’s only so much use to spinning pies around.
  本题的其他回答提供了从 $\mathbb{R}$ 构造 $\mathbb{C}$ 的不同视角，还讨论了复数的用途和价值 —— 毕竟 “旋转派” 的例子只能说明一部分问题。
• A Visual, Intuitive Guide to Imaginary Numbers — thanks go to Joe, in the comments, for pointing this out to me.
  《虚数的可视化直观指南》—— 感谢评论区的乔向我推荐这篇文章。

I’d be glad to know of more such resources; feel free to post any in the comments.
如果有更多这类资源，欢迎在评论区分享，我很乐意了解。

answered Sep 20, 2012 at 13:01
Clive Newstead

+1 but you didn’t complete the definition that the imaginary number line as simply the axis orthogonal to the real number line in the complex number plane so that every complex number can be expressed as the sum of a real number and an imaginary number.
+1，但你没完整定义 “虚数轴”：它是复数平面中与实数轴垂直的轴，因此每个复数都能表示为一个实数与一个虚数的和。

– StarNamer
Commented Sep 20, 2012 at 14:59

Excellent explanation! The first time I’ve seen the analogy of rotation was here, which also contains a really good, visual exploration of imaginary numbers: betterexplained.com/articles/…
解释得太棒了！我第一次看到 “旋转” 类比是在这篇文章里，它还对虚数做了非常好的可视化探索：betterexplained.com/articles/…

– Joe
Commented Sep 20, 2012 at 15:01

You ask why imaginary numbers are useful. As with most extensions of number systems, historically such generalizations were invented because they help to simplify certain phenomena in existing number systems. For example, negative numbers and fractions permit one to state in a single general form the quadratic equation and its solution (older solutions bifurcated into many cases, avoiding negative numbers and fractions). One of the primary reasons motivating the invention of complex numbers is that they serve to linearize what would otherwise be nonlinear phenomena — thus greatly simplifying many problems. Here are some examples.
你问虚数有什么用。和大多数数系扩展一样，历史上发明这类推广是因为它们能简化现有数系中的某些复杂现象。比如，负数和分数让一元二次方程及其解能以统一的一般形式表示（早期解法为了回避负数和分数，会分成多种情况讨论）。而发明复数的主要原因之一，是它能将原本的 “非线性” 现象 “线性化”—— 从而大幅简化许多问题。以下是一些例子。

Consider the problem of representing integers as sums of squares $n=x^2+y^2$. Early solutions to this and related problems employed a complicated arithmetic of binary quadratic forms. Such arithmetic was quite intricate and often very nonintuitive, e.g. even the proof of associativity of composition of such forms was a tour de brute force, occupying pages of unmotivated computations in Gauss’ Disq. Arith. But this quadratic arithmetic of binary quadratic forms can be linearized. Indeed, by factorization $x^2+y^2=(x+yi)(x-yi)$, which allows us to view sums of squares as norms of Gaussian integers $x+yi$，$x,y\in \mathbb{Z}$. But just like the rational integers $\mathbb{Z}$, these “imaginary” integers have a Euclidean algorithm, so enjoy unique factorization into primes. By considering all the possible factorizations of $n$ in the Gaussian integers we obtain all the possible representations of $n$ as a sum of squares. In a similar way, “rational, real” arithmetic of integral quadratic forms becomes much simpler by passing to the “irrational” and/or “imaginary” arithmetic of quadratic number fields. This line of research led to the discovery of ideals and modules, fundamental linear structures at the heart of modern number theory and algebra. [See this answer and its links for a more precise description of the equivalence between quadratic forma and ideals].
考虑 “将整数表示为两个平方和” 的问题，即 $n=x^2+y^2$。早期解决这类问题及相关问题时，采用的是复杂的 “二元二次型算术”。这种算术非常繁琐且缺乏直观性，例如，即使是 “二次型合成的结合律” 证明，也需要大量复杂计算 —— 在高斯的《算术研究》中，这部分内容占了好几页，且计算动机不明确。但这种 “二次型算术” 可以被 “线性化”：通过因式分解 $x^2+y^2=(x+yi)(x-yi)$，我们能将 “平方和” 视为 “高斯整数”$x+yi$（其中 $x,y\in \mathbb{Z}$）的范数。而这些 “虚整数” 和有理数整数 $\mathbb{Z}$ 一样，具有欧几里得算法，因此满足 “唯一素因子分解”。通过考虑 $n$ 在高斯整数中的所有可能分解，我们就能得到 $n$ 表示为平方和的所有形式。类似地，将 “整二次型的有理、实数算术” 转化为 “二次数域的无理、虚数算术” 后，运算会变得简单得多。这一研究方向最终促成了 “理想” 和 “模” 的发现 —— 它们是现代数论和代数学核心的 “线性” 结构。[关于二次型与理想的等价性，可参考 此回答 及其链接获取更精确的描述。]

Thus, by factorizing completely over $\mathbb{C}$, we have reduced the complicated nonlinear arithmetic of binary quadratic forms to the simpler, linear arithmetic of Gaussian integers, i.e. to the more familiar arithmetical structure of a unique factorization domain (in fact a Euclidean domain). Analogous linearization serves to simplify many problems. For example, when integrating or summing rational functions (quotients of polynomials), by factoring denominators over $\mathbb{C}$ (vs. $\mathbb{R}$) and taking partial fraction decompositions, the denominators are at worst powers of linear (vs. quadratic) polynomials — which greatly simplifies matters. More generally, when solving constant coefficient differential or difference equations (recurrences), by factoring their characteristic (operator) polynomials over $\mathbb{C}$, we reduce to solutions of linear (vs. quadratic) differential or difference equations. In the same way, there are many real problems (over $\mathbb{R}$) whose simplest solutions are obtained by an imaginary detour (over $\mathbb{C}$). Perhaps readers will mention more such problems in the comments.
因此，通过在 $\mathbb{C}$ 上进行完全因式分解，我们将复杂的 “二元二次型非线性算术” 简化为更简单的 “高斯整数线性算术”—— 即更熟悉的 “唯一分解整环（实际上是欧几里得整环）” 算术结构。类似的线性化方法还能简化许多其他问题。例如，在对有理函数（多项式的商）积分或求和时，若将分母在 $\mathbb{C}$（而非 $\mathbb{R}$）上因式分解并进行部分分式分解，分母最多是 “一次多项式的幂”（而非 “二次多项式”）—— 这会大幅简化计算。更一般地，在求解常系数微分方程或差分方程（递推关系）时，将其特征（算子）多项式在 $\mathbb{C}$ 上因式分解后，可将方程简化为 “线性微分 / 差分方程”（而非 “二次方程”）求解。同样，许多在 $\mathbb{R}$ 上的实际问题，其最简单的解法需要 “绕道 $\mathbb{C}$” 才能得到。读者若知道更多此类例子，欢迎在评论区补充。

answered Sep 20, 2012 at 15:33
Bill Dubuque

That’s up to now by far the best answer about the usefulness. +1
这是目前为止关于 “虚数用途” 的最佳回答。

– celtschk
Commented Sep 20, 2012 at 15:56

Beautifully stated. I wasn’t aware of the Gaussian integers, very cool
解释得很精彩！我以前不知道高斯整数，太有意思了。

– acjay
Commented Sep 20, 2012 at 23:26

---

A Visual, Intuitive Guide to Imaginary Numbers

虚数的可视化直观指南

Imaginary numbers always confused me. Like understanding e, most explanations fell into one of two categories:
虚数总让我感到困惑。就像理解自然常数 $e$ 一样，大多数解释都逃不出以下两类：

• It’s a mathematical abstraction, and the equations work out. Deal with it.
  它是一种数学抽象概念，方程运算结果是成立的，接受这一点就行。

• It’s used in advanced physics, trust us. Just wait until college.
  它会用在高阶物理中，相信我们，等上了大学你就懂了。

Gee, what a great way to encourage math in kids! Today we’ll assault this topic with our favorite tools:
哎，这可真是鼓励孩子学习数学的 “好方法” 啊！这里，我们将用以下几个最顺手的工具来攻克这个主题：

• Focusing on relationships, not mechanical formulas.
  聚焦关系本质，而非机械的公式。

• Seeing complex numbers as an upgrade to our number system, just like zero, decimals and negatives were.
  将复数视为数字系统的一次升级，就像当初引入零、小数和负数一样。

• Using visual diagrams, not just text, to understand the idea.
  借助可视化图表，而非单纯依赖文字，来理解这个概念。

And our secret weapon: learning by analogy. We’ll approach imaginary numbers by observing its ancestor, the negatives. Here’s your guidebook:
我们还有一个秘密武器：类比学习法。我们会从虚数的 “前辈”—— 负数入手，逐步理解虚数。这是为你准备的参考表：

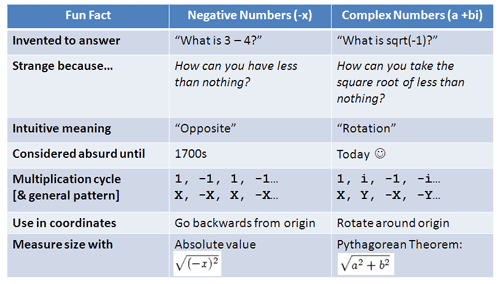
It doesn’t make sense yet, but hang in there. By the end we’ll hunt down $i$ and put it in a headlock, instead of the reverse.
现在看不懂没关系，耐心往下看。到最后，我们会彻底搞懂 $i$，让它 “任我们摆布”，而不是被它难住。

Really Understanding Negative Numbers

真正理解负数

Negative numbers aren’t easy. Imagine you’re a European mathematician in the 1700s. You have $3$ and $4$, and know you can write $4–3=1$. Simple.
负数并不容易理解。试想一下，你是 18 世纪的一位欧洲数学家，你知道数字 $3$ 和 $4$，也知道可以写出算式 $4–3=1$，这很简单。

But what about $3-4$? What, exactly, does that mean? How can you take $4$ cows from $3$? How could you have less than nothing?
但如果是 $3-4$ 呢？这到底是什么意思？你怎么从 $3$ 头牛里牵走 $4$ 头？怎么可能存在 “比没有还少” 的情况呢？

Negatives were considered absurd, something that “darkened the very whole doctrines of the equations” (Francis Maseres, 1759). Yet today, it’d be absurd to think negatives aren’t logical or useful. Try asking your teacher whether negatives corrupt the very foundations of math.
在当时，负数被认为是荒谬的，是 “使方程的整个理论体系都变得晦涩难懂” 的东西（弗朗西斯・马塞雷斯，1759 年）。但如今，要是有人觉得负数不符合逻辑、没有用处，才是荒谬的。你可以试着问老师 “负数会不会破坏数学的基础”，看看老师会怎么说。

What happened? We invented a theoretical number that had useful properties. Negatives aren’t something we can touch or hold, but they describe certain relationships well (like debt). It was a useful fiction.
这一切是怎么改变的？因为我们发明了一种 “具有实用性质的理论数字”。负数无法被触摸或持有，但它能很好地描述某些关系（比如债务），是一种有用的 “虚构概念”。

Rather than saying “I owe you 30” and reading words to see if I’m up or down, I can write “$-30$” and know it means I’m in the hole. If I earn money and pay my debts ($-30+100=70$), I can record the transaction easily. I have $+70$ afterwards, which means I’m in the clear.
与其说 “我欠你 30（单位货币）”，还要通过文字判断自己是 “欠着钱” 还是 “有钱剩”，不如直接写成 “$-30$”，这样一眼就知道自己处于负债状态。如果我赚了钱并还清债务（$-30+100=70$），也能轻松记录这笔交易。最终结果是 $+70$，说明我还清了债务，没有欠款了。

The positive and negative signs automatically keep track of the direction — you don’t need a sentence to describe the impact of each transaction. Math became easier, more elegant. It didn’t matter if negatives were “tangible” — they had useful properties, and we used them until they became everyday items. Today you’d call someone obscene names if they didn’t “get” negatives.
正负号会自动记录 “方向”—— 无需用一句话来描述每笔交易的影响，数学因此变得更简单、更简洁。负数是否 “可触摸” 并不重要，重要的是它有实用价值。我们一直使用它，直到它成为日常中随处可见的概念。如今，如果有人 “搞不懂” 负数，你可能都会觉得不可思议。

But let’s not be smug about the struggle: negative numbers were a huge mental shift. Even Euler, the genius who discovered $e$ and much more, didn’t understand negatives as we do today. They were considered “meaningless” results (he later made up for this in style).
但我们也不必为现在能理解负数而沾沾自喜：理解负数其实是一次巨大的思维转变。即便是发现了自然常数 $e$ 等众多成果的天才数学家欧拉，当初对负数的理解也不如我们现在深刻。在当时，负数被认为是 “无意义” 的结果（不过后来他用出色的研究弥补了这一认知差距）。

It’s a testament to our mental potential that today’s children are expected to understand ideas that once confounded ancient mathematicians.
如今的孩子需要理解那些曾让古代数学家困惑不已的概念，这足以证明人类的思维潜力是多么强大。

Enter Imaginary Numbers

虚数的登场

Imaginary numbers have a similar story. We can solve equations like this all day long:
虚数的 “诞生” 故事与此相似。我们可以轻松解出如下这样的方程：
$$x^2=9$$

The answers are $3$ and $-3$. But suppose some wiseguy puts in a teensy, tiny minus sign:
答案是 $3$ 和 $-3$。但要是有个爱挑刺的人在等式右边加一个小小的负号，变成这样：

$$x^2=-9$$

Uh oh. This question makes most people cringe the first time they see it. You want the square root of a number less than zero? That’s absurd! (Historically, there were real questions to answer, but I like to imagine a wiseguy.)
哦，这下麻烦了。大多数人第一次看到这个方程都会皱起眉头。你想求一个负数的平方根？这也太荒谬了吧！（从历史角度看，当时确实有需要解决的实际问题，但我还是愿意想象这是某个爱挑刺的人提出来的）。

It seems crazy, just like negatives, zero, and irrationals (non-repeating numbers) must have seemed crazy at first. There’s no “real” meaning to this question, right?
这看起来很离谱，但就像当初的负数、零和无理数（无限不循环小数）一样，刚出现时都让人觉得离谱。这个问题似乎没有 “实际” 意义，对吧？

Wrong. So-called “imaginary numbers” are as normal as every other number (or just as fake): they’re a tool to describe the world. In the same spirit of assuming $-1$, $.3$, and $0$ “exist”, let’s assume some number $i$ exists where:
不对。所谓的 “虚数” 和其他任何数字一样正常（或者说一样 “虚构”）：它只是一种描述世界的工具。就像我们默认 $-1$、$0.3$ 和 $0$“存在” 一样，我们也可以假设存在一个数字 $i$，满足：

$$i^2=-1$$

That is, you multiply $i$ by itself to get $-1$. What happens now?
也就是说，$i$ 乘以它本身结果等于 $-1$。接下来会发生什么呢？

Well, first we get a headache. But playing the “Let’s pretend $i$ exists” game actually makes math easier and more elegant. New relationships emerge that we can describe with ease.
首先，我们可能会觉得头疼。但只要愿意 “假设 $i$ 存在”，数学反而会变得更简单、更简洁，一些新的关系也会随之出现，让我们能轻松描述。

You may not believe in $i$, just like those fuddy old mathematicians didn’t believe in $-1$. New, brain-twisting concepts are hard and they don’t make sense immediately, even for Euler. But as the negatives showed us, strange concepts can still be useful.
你可能不相信 $i$ 的存在，就像当初那些古板的数学家不相信 $-1$ 存在一样。那些新颖、让人绞尽脑汁的概念往往很难理解，也无法立刻体现出意义，即便是欧拉也不例外。但正如负数的例子所证明的，看似奇怪的概念也能有很大用处。

I dislike the term “imaginary number” — it was considered an insult, a slur, designed to hurt $i$‘s feelings. The number $i$ is just as normal as other numbers, but the name “imaginary” stuck so we’ll use it.
我不太喜欢 “虚数” 这个术语 —— 它最初带有贬义，像是一种侮辱，仿佛在 “贬低”$i$ 的 “地位”。实际上，$i$ 和其他数字一样正常，但 “虚数” 这个名字已经沿用下来，所以我们还是会使用它。

Visual Understanding of Negative and Complex Numbers

从可视化角度理解负数与复数

Equations ask questions. When you see
方程本质上是在提出问题。当你看到

$x^2=9$

It’s more than just a plug and chug problem. Think about the question like this:
它不只是一个套公式计算的问题。可以这样理解这个问题：

$1\cdot x^2=9$

What transformation (“times $x$”), when applied twice, will turn $1$ into $9$?
哪种 变换（即 “乘以 $x$”），连续应用两次后，能将 $1$ 变成 $9$？

We have two answers:
答案有两个：

• Scale by $3$ (times $3$): Do it twice and you’ll get $9$: $1\cdot 3\cdot 3=9$
  放大 $3$ 倍（乘以 $3$）：连续应用两次就能得到 $9$：$1\cdot 3\cdot 3=9$
   
• Scale by $3$ and flip (times $-3$): Done twice, you get $9$ also: $1\cdot (-3)\cdot (-3)=9$
  放大 $3$ 倍并翻转（乘以 $-3$）：连续应用两次，同样能得到 $9$：$1\cdot (-3)\cdot (-3)=9$
   
  Nifty. I included “$1$” to show what is being transformed. Sure, it’s optional, but it’s not something we think about. What is the “times $3$” acting on?
  很巧妙吧？我特意加入 “$1$”，是为了明确 被变换的对象 是什么。当然，这一步并非必需，但却是我们常常忽略的点：“乘以 $3$” 这个运算，到底作用在什么之上？
   
  Stepping back this way, we can see arithmetic as a method to push, pull, tug and squeeze one number into another. We’ve managed to turn one large transformation (“times $9$”) into two equal, smaller ones (“times $-3$” or “times $3$”).
  从这个角度退一步看，我们会发现算术其实是一种 “将一个数字转化为另一个数字” 的方法 —— 可以是 “推”“拉”“拽” 或 “压缩”。我们成功地将一个复杂的变换（“乘以 $9$”），拆解成了两个相同的、更简单的变换（“乘以 $-3$” 或 “乘以 $3$”）。

A s described above, the equation $x^2=9$ really means:

如上所述，方程 $x^2=9$ 的实际含义是：
$$1\cdot x^2=9$$

or
或者
$$1\cdot x\cdot x=9$$

• What transformation $x$, when applied twice, turns $1$ to $9$?
  对数字 $1$ 施加两次变换 $x$ 后，能得到 $9$，那么这个变换 $x$ 是什么？

The two answers are “$x=3$” and “$x=-3$”: That is, you can “scale by” $3$ or “scale by $3$ and flip” (flipping or taking the opposite is one interpretation of multiplying by a negative).
答案有两个：“$x=3$” 和 “$x=-3$”。也就是说，你可以 “将 $1$ 放大 $3$ 倍”，或者 “将 $1$ 放大 $3$ 倍后再翻转”（“翻转” 或 “取相反数” 是对 “乘以负数” 的一种解读）。

Now let’s think about $x^2=-1$, which is really
现在我们来思考方程 $x^2=-1$，它的实际含义是：

$$1\cdot x\cdot x=-1$$

• What transformation $x$, when applied twice, turns $1$ into $-1$? Hrm.
  对数字 $1$ 施加两次变换 $x$ 后，能得到 $-1$，那么这个变换 $x$ 是什么？* 这有点难办。

• We can’t multiply by a positive twice, because the result stays positive
  我们不能两次都乘以正数，因为结果始终是正数。

• We can’t multiply by a negative twice, because the result will flip back to positive on the second multiplication
  我们也不能两次都乘以负数，因为第二次乘以负数时，结果会翻转为正数。

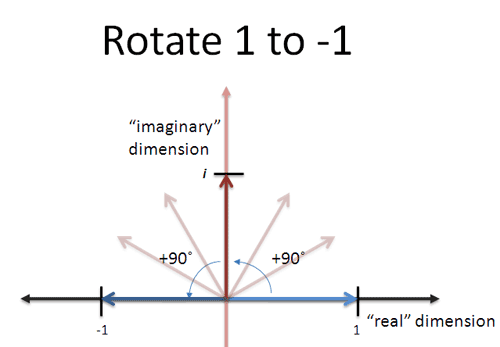
But what about… arotation! It sounds crazy, but if we imagine $x$ being a “rotation of $90$ degrees”, then applying $x$ twice will be a $180$ degree rotation, or a flip from $1$ to $-1$!
但如果是……旋转呢！这听起来很疯狂，但要是我们把 $x$ 想象成 “旋转 $90$ 度”，那么施加两次 $x$ 变换就是旋转 $180$ 度，正好能让 $1$“翻转” 成 $-1$！

Yowza! And if we think about it more, we could rotate twice in the other direction (clockwise) to turn $1$ into $-1$. This is “negative” rotation or a multiplication by $-i$:
哇哦！再仔细想想，我们也可以向另一个方向（顺时针）旋转两次，同样能让 $1$ 变成 $-1$。这就是 “反向旋转”，相当于乘以 $-i$：

If we multiply by $-i$ twice, the first multiplication would turn $1$ into $-i$, and the second turns $-i$ into $-1$. So there’s really two square roots of $-1$: $i$ and $-i$.
如果我们两次都乘以 $-i$，第一次相乘会让 $1$ 变成 $-i$，第二次相乘会让 $-i$ 变成 $-1$。所以，$-1$ 其实有两个平方根：$i$ 和 $-i$。

This is pretty cool. We have some sort of answer, but what does it mean?
这太有意思了。我们已经找到了答案，但这到底意味着什么呢？

• $i$ is a “new imaginary dimension” to measure a number
  $i$ 是衡量数字的一个 “新的虚数维度”。

• $i$ (or $-i$) is what numbers “become” when rotated
  $i$（或 $-i$）是数字经过旋转后 “变成” 的结果。

• Multiplying by $i$ is a rotation by $90$ degrees counter-clockwise
  乘以 $i$ 相当于将数字逆时针旋转 $90$ 度。

• Multiplying by $-i$ is a rotation of $90$ degrees clockwise
  乘以 $-i$ 相当于将数字顺时针旋转 $90$ 度。

• Two rotations in either direction is $-1$: it brings us back into the “regular” dimensions of positive and negative numbers.
  向任意一个方向旋转两次，结果都等于 $-1$：这会让我们回到正数和负数所在的 “常规” 维度。

**Numbers are 2-dimensional.*Yes, it’s mind bending, just like decimals or long division would be mind-bending to an ancient Roman. (What do you mean there’s a number between $1$ and $2$?). It’s a strange, new way to think about math.
数字是二维的。没错，这让人难以理解，就像小数或长除法对于古罗马人来说难以理解一样（ 你说 $1$ 和 $2$ 之间还有数字是什么意思？*）。但这确实是一种新颖的数学思维方式。

We asked “How do we turn $1$ into $-1$ in two steps?” and found an answer: rotate it $90$ degrees. It’s a strange, new way to think about math. But it’s useful. (By the way, this geometric interpretation of complex numbers didn’t arrive until [decades](https://www.crsd.org/cms/lib5/PA01000188/Centricity/Domain/3021/TIMELINE OF i.pdf) after $i$ was discovered).
我们曾问 “如何通过两步操作将 $1$ 变成 $-1$？”，现在找到了答案：将它旋转 $90$ 度。这虽然是一种新颖的数学思维方式，但很有用。（顺便提一句，这种对复数的几何解读，在 $i$ 被发现后的几十年才出现。）

Also, keep in mind that having counter-clockwise be positive is a human convention — it easily could have been the other way.
另外要记住，将逆时针方向定为 “正方向” 是人类的约定俗成 —— 其实定为顺时针方向也完全可行。

Finding Patterns

寻找规律

Let’s dive into the details a bit. When multiplying negative numbers (like $-1$), you get a pattern:
我们来深入看看细节。当我们反复乘以负数（比如 $-1$）时，会呈现出这样的规律：

• $1$, $-1$, $1$, $-1$, $1$, $-1$, $1$, $-1$

Since $-1$ doesn’t change the size of a number, just the sign, you flip back and forth. For some number “$x$”, you’d get:
因为 $-1$ 不会改变数字的大小，只会改变符号，所以结果会在正负之间来回切换。对于任意数字 “$x$”，反复乘以 $-1$ 会得到：

• $x$, $-x$, $x$, $-x$, $x$, $-x$…

This idea is useful. The number “$x$” can represent a good or bad hair week. Suppose weeks alternate between good and bad; this is a good week; what will it be like in $47$ weeks?
这个规律很有用。比如，我们可以用 “$x$” 表示 “头发状态好的一周”，用 “$-x$” 表示 “头发状态差的一周”。假设头发状态每周在 “好” 和 “差” 之间交替，本周头发状态很好，那么 $47$ 周后头发状态会怎么样？

$$x\cdot (-1{)}^{47}=x\cdot -1=-x$$

So $-x$ means a bad hair week. Notice how negative numbers “keep track of the sign”: we can throw $(-1{)}^{47}$ into a calculator without having to count (”Week $1$ is good, week $2$ is bad… week $3$ is good…“). Things that flip back and forth can be modeled well with negative numbers.
结果是 $-x$，说明 $47$ 周后头发状态会很差。可以看到，负数能 “记录符号变化”：我们只需计算 $(-1{)}^{47}$，不用逐周数 “第 $1$ 周好，第 $2$ 周差…… 第 $3$ 周好……”。对于这种 “来回切换” 的情况，用负数建模非常合适。

Ok. Now what happens if we keep multiplying by $i$?
好的，现在我们来看看反复乘以 $i$ 会出现什么情况：

$$1,i,i^2,i^3,i^4,i^5$$

Very funny. Let’s reduce this a bit:
很有意思吧？我们来简化一下这些结果：

• $1=1$
  No questions here
  这一点毫无疑问

• $i=i$
  Can’t do much
  无法进一步简化

• $i^2=-1$
  That’s what $i$ is all about
  这正是 $i$ 的定义

• $i^3=(i\cdot i)\cdot i=-1\cdot i=-i$
  Ah, $3$ rotations counter-clockwise = $1$ rotation clockwise. Neat.
  啊，逆时针旋转 $3$ 次相当于顺时针旋转 $1$ 次，真巧妙

• $i^4=(i\cdot i)\cdot (i\cdot i)=-1\cdot -1=1$

  4 rotations bring us “full circle”
  旋转 $4$ 次后回到 “初始位置”

• $i^5=i^4\cdot i=1\cdot i=i$
  Here we go again…
  又开始循环了……

Represented visually:
用图表展示如下：

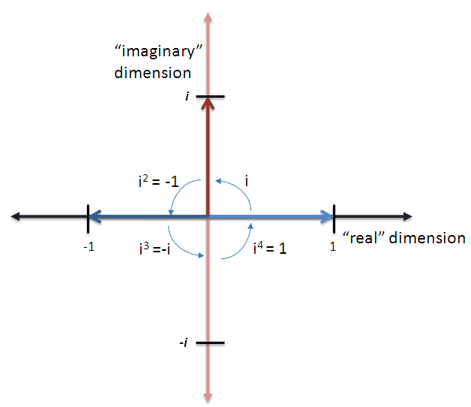
We cycle every $4$th rotation. This makes sense, right? Any kid can tell you that $4$ left turns is the same as no turns at all. Now rather than focusing on imaginary numbers ($i$, $i^2$), look at the general pattern:
每旋转 $4$ 次就会完成一个循环。这很合理，对吧？就连小孩都知道，向左转 $4$ 次和没转弯是一样的。现在，我们别只盯着虚数（$i$、$i^2$ 等），看看整体规律：

• $X$, $Y$, $-X$, $-Y$, $X$, $Y$, $-X$, $-Y$…

Like negative numbers modeling flipping, imaginary numbers can model anything that rotates between two dimensions “$X$” and “$Y$”. Or anything with a cyclic, circular relationship — have anything in mind?
就像负数可以用来建模 “来回切换” 的情况一样，虚数可以用来建模任何在 “$X$” 和 “$Y$” 两个维度之间旋转的事物，或者任何具有循环、圆周关系的事物 —— 你能想到什么例子吗？

‘Cos it’d be a sin if you didn’t. There’ll de Moivre be more in future articles. [Editor’s note: Kalid is in electroshock therapy to treat his pun addiction.]
要是想不出来，可就太 “遗憾”（$\sin$，双关 “正弦”）了。未来的文章中，我们还会讲到棣莫弗公式（de Moivre，双关 “还会有更多”）。[编者注：卡利德（本文作者）因沉迷谐音梗，正在接受电休克治疗。]

Understanding Complex Numbers

理解复数

There’s another detail to cover: can a number be both “real” and “imaginary”?
还有一个细节要讲：一个数字能不能既 “实” 又 “虚”？

You bet. Who says we have to rotate the entire $90$ degrees? If we keep $1$ foot in the “real” dimension and another in the imaginary one, it looks like this:
当然可以！谁说我们一定要旋转整整 $90$ 度？如果我们一只脚踩在 “实” 维度，另一只脚踩在 “虚” 维度，就会是这样的：

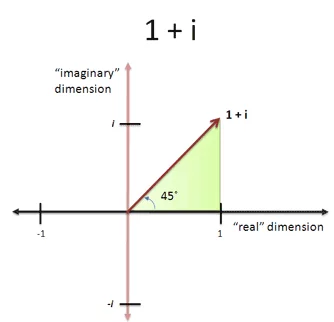
We’re at a $45$ degree angle, with equal parts in the real and imaginary ($1+i$). It’s like a hotdog with both mustard and ketchup — who says you need to choose?
我们处于 $45$ 度角的位置，实部和虚部的占比相等（即 $1+i$）。这就像热狗既加芥末又加番茄酱一样 —— 谁说只能选一种？

In fact, we can pick any combination of real and imaginary numbers and make a triangle. The angle becomes the “angle of rotation”. A complex number is the fancy name for numbers with both real and imaginary parts. They’re written $a+bi$, where
实际上，我们可以任意组合实部和虚部的数值，构成一个三角形，其中的角度就是 “旋转角”。这种同时包含实部和虚部的数字，有一个专业的名字叫 “复数”，通常写成 $a+bi$ 的形式，其中：

• $a$ is the real part
  $a$ 是实部

• $b$ is the imaginary part
  $b$ 是虚部

Not too bad. But there’s one last question: how “big” is a complex number? We can’t measure the real part or imaginary parts in isolation, because that would miss the big picture.
听起来还不错吧？但还有最后一个问题：复数的 “大小” 该如何衡量？我们不能孤立地衡量实部或虚部的大小，因为那样会忽略整体情况。

Let’s step back. The size of a negative number is not whether you can count it — it’s the distance from zero. In the case of negatives this is:
我们先退一步想想。负数的 “大小” 不在于它能否被计数，而在于它到原点 $0$ 的距离。对于负数来说，其大小的计算方式是：

$$\text{Size of }-x=\sqrt{(-x{)}^2}=|x|$$

Which is another way to find the absolute value. But for complex numbers, how do we measure two components at $90$ degree angles?
这其实就是求负数绝对值的另一种方式。但对于复数，我们该如何衡量两个呈 $90$ 度角的分量所构成的整体大小呢？

• It’s a bird… it’s a plane… it’s Pythagoras!
  是鸟…… 是飞机…… 不对，是勾股定理！*

Geez, his theorem shows up everywhere, even in numbers invented $2000$ years after his time. Yes, we are making a triangle of sorts, and the hypotenuse is the distance from zero:
天呐，勾股定理真是无处不在，就算是在毕达哥拉斯死后 $2000$ 年才被发明的数字中，也能见到它的身影。没错，我们可以将复数看作一个直角三角形，其斜边的长度就是复数到原点 $0$ 的距离：
$$\text{Size of }a+bi=\sqrt{a^2+b^2}$$

Neat. While measuring the size isn’t as easy as “dropping the negative sign”, complex numbers do have their uses. Let’s take a look.
真巧妙！虽然复数的大小计算不像负数那样 “去掉负号” 就行，但复数确实有它的用武之地。我们来看一个例子。

A Real Example: Rotations

实际例子：旋转问题

We’re not going to wait until college physics to use imaginary numbers. Let’s try them out today. There’s much more to say about complex multiplication, but keep this in mind:
我们不用等到大学学物理时才用虚数，今天就来实际用用看。关于复数乘法，还有很多内容可以讲，但先记住这一点：

• Multiplying by a complex number rotates by its angle
  乘以一个复数，相当于将原复数按该复数的角度旋转

Let’s take a look. Suppose I’m on a boat, with a heading of $3$ units East for every $4$ units North. I want to change my heading $45$ degrees counter-clockwise. What’s the new heading?
我们来看这个例子：假设我在船上，航向是 “每向正北行驶 $4$ 个单位，就向正东行驶 $3$ 个单位”。现在我想将航向逆时针旋转 $45$ 度，新的航向会是什么？

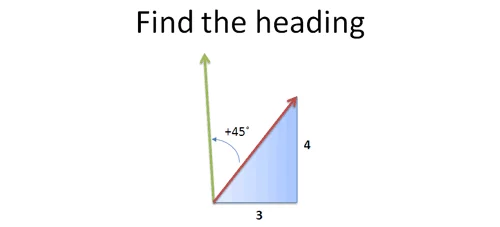
Some hotshot will say “That’s simple! Just take the sine, cosine, gobbledegook by the tangent… fluxsom the foobar… and…“.Crack. Sorry, did I break your calculator? Care to answer that question again?
有些 “高手” 可能会说：“这还不简单！用正弦、余弦，再用正切算一堆乱七八糟的…… 然后就能得到结果……”。咔嚓。抱歉，我是不是把你的计算器弄坏了？要不你再试着回答一次？

Let’s try a simpler approach: we’re on a heading of $3+4i$ (whatever that angle is; we don’t really care), and want to rotate by $45$ degrees. Well, $45$ degrees is $1+i$ (perfect diagonal), so we can multiply by that amount!
我们换个更简单的方法：我们的航向可以表示为 $3+4i$（不管它对应的角度是多少，我们其实不在乎），现在要旋转 $45$ 度。而 $45$ 度对应的复数是 $1+i$（正好是对角线方向），所以我们只需将两个复数相乘就行了！

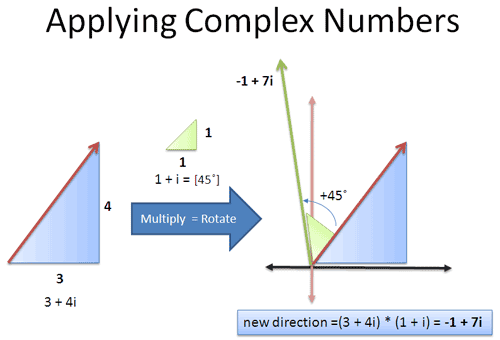
Here’s the idea:
思路是这样的：

• Original heading: $3$ units East, $4$ units North = $3+4i$
  原航向：向正东 $3$ 个单位，向正北 $4$ 个单位 = $3+4i$

• Rotate counter-clockwise by $45$ degrees = multiply by $1+i$. (Here’s why multiplication, not addition, performs the rotation.)
  逆时针旋转 $45$ 度 = 乘以 $1+i$。（原因：实现旋转的是乘法，而非加法。）

If we multiply them together we get:
若将两者相乘，结果如下：

$$\begin{array}{rl}(3+4i)\cdot (1+i)& =3+3i+4i+4i^2\\ & =3+7i+4(-1)\\ & =-1+7i\end{array}$$

So our new orientation is $1$ unit West ($-1$ East), and $7$ units North, which you could draw out and follow.
所以新的航向是 “向正西 $1$ 个单位（即向东 $-1$ 个单位），向正北 $7$ 个单位”，你可以画出来并照着这个方向行驶。

But yowza! We found that out in $10$ seconds, without touching sine or cosine. There were no vectors, matrices, or keeping track what quadrant we are in. It was just arithmetic with a touch of algebra to cross-multiply. Imaginary numbers have the rotation rules baked in: it just works.
哇哦！我们只用了 $10$ 秒钟就算出了结果，全程没用到正弦或余弦，也没用到向量、矩阵，更不用记自己在哪个象限。这只是简单的算术运算，再加上一点代数中的交叉相乘。虚数已经把旋转规则 “内置” 进去了：就是这么好用。

Even better, the result is useful. We have a heading ($-1$, $7$) instead of an angle ($\arctan (7/-1)=98.13$, keeping in mind we’re in quadrant $2$). How, exactly, were you planning on drawing and following that angle? With the protractor you keep around?
更棒的是，这个结果非常实用。我们得到的是一个具体的航向（$-1$，$7$），而不是一个角度（$\arctan (7/-1)=98.13$ 度，还要记住是在第二象限）。你难道打算用随身携带的量角器画出 $98.13$ 度，然后照着这个角度行驶吗？

No, you’d convert it into cosine and sine ($-.14$ and $.99$), find a reasonable ratio between them (about $1$ to $7$), and sketch out the triangle. Complex numbers beat you to it, instantly, accurately, and without a calculator.
显然不会。你肯定会把角度转换成余弦和正弦值（$-0.14$ 和 $0.99$），再找出它们之间的大致比例（约为 $1:7$），然后画出这个三角形。而复数直接一步到位，又快又准，还不用计算器。

If you’re like me, you’ll find this use mind-blowing. And if you don’t, well, I’m afraid math doesn’t toot your horn. Sorry.
如果你和我一样，就会觉得这个用法太神奇了。要是你不这么觉得，那恐怕数学确实不是你的 “菜”，抱歉啦。

Trigonometry is great, but complex numbers can make ugly calculations simple (like calculating $\cos (a+b)$ ). This is just a preview; later articles will give you the full meal.
三角学固然很棒，但复数能让复杂的计算变简单（比如计算 $\cos (a+b)$）。今天只是小试牛刀，后续文章会为你详细讲解。

Aside:Some people think “Hey, it’s not useful to have North/East headings instead of a degree angle to follow!”
补充说明：有些人可能会想 “喂，用‘正北 / 正东’的航向，还不如用角度来得方便吧！”

Really? Ok, look at your right hand. What’s the angle from the bottom of your pinky to the top of your index finger? Good luck figuring that out on your own.
真的吗？那好，看看你的右手：从小指根部到食指指尖的角度是多少？祝你能自己算出来。

With a heading, you can at least say “Oh, it’s $X$ inches across and $Y$ inches up” and have some chance of working with that bearing.
而用航向的话，你至少能说 “哦，横向距离是 $X$ 英寸，纵向距离是 $Y$ 英寸”，这样反而能更轻松地确定方位。

Complex Numbers Aren’t

复数不是什么

That was a whirlwind tour of my basic insights. Take a look at the first chart — it should make sense now.
以上就是我对复数的一些基本理解，算是快速入门。再回头看看最开始的参考表，现在应该能看懂了吧。

There’s so much more to these beautiful, zany numbers, but my brain is tired. My goals were simple:
这些既美妙又 “古怪” 的数字，还有很多值得探索的地方，但我已经有点累了。我写这篇文章的目标很简单：

• Convince you that complex numbers were considered “crazy” but can be useful (just like negative numbers were)
  让你相信，复数虽然曾被认为 “荒谬”，但和负数一样，具有很大的实用价值。

• Show how complex numbers can make certain problems easier, like rotations
  向你展示复数如何让某些问题（比如旋转问题）变得更简单。

If I seem hot and bothered about this topic, there’s a reason. Imaginary numbers have been a bee in my bonnet for years— the lack of an intuitive insight frustrated me.
要是我在这个话题上显得有些激动，是有原因的。虚数曾困扰了我好多年—— 一直找不到直观的理解方式，这让我很沮丧。

Now that I’ve finally had insights, I’m bursting to share them. But it frustrates me that you’re reading this on the blog of a wild-eyed lunatic, andnotin a classroom. We suffocate our questions and “chug through” — because we don’t search for and share clean, intuitive insights. Egad.
现在我终于搞懂了，迫不及待想分享出来。但让我沮丧的是，你是在一个 “狂热分子” 的博客上读到这些内容，而不是在课堂上。我们总是压抑自己的疑问，“硬着头皮” 学 —— 因为我们没有去寻找和分享那些清晰、直观的理解方式。天啊！

But better to light a candle than curse the darkness: here’s my thoughts, and one of you will shine a spotlight. Thinking we’ve “figured out” a topic like numbers is what keeps us in Roman Numeral land.
但与其抱怨黑暗，不如点亮蜡烛：以上是我的思考，希望有人能在此基础上进一步深入。如果认为我们已经 “彻底搞懂” 了数字这类主题，就会像困在罗马数字时代一样停滞不前。

Epilogue: But they’re still strange!

后记：但复数还是很奇怪！

I know, they’re still strange to me too. I try to put myself in the mind of the first person to discover zero.
我知道，复数对我来说还是有点奇怪。我试着换位思考，想象第一个发现 “零” 的人当时的感受。

Zero is such a weird idea, having “something” represent “nothing”, and it eluded the Romans. Complex numbers are similar — it’s a new way of thinking. But both zero and complex numbers make math much easier. If we never adopted strange, new number systems, we’d still be counting on our fingers.
“用某个东西代表‘什么都没有’”，零的概念曾经也很奇怪，古罗马人就一直无法理解。复数与此类似 —— 它是一种新的思维方式。但零和复数都让数学变得更简单。如果我们一直不接受这些奇怪的新数字系统，现在可能还在掰手指计数。

I repeat this analogy because it’s so easy to start thinking that complex numbers aren’t “normal”. Let’s keep our mind open: in the future they’ll chuckle that complex numbers were once distrusted, even until the 2000’s.
我反复用这个类比，是因为人们很容易觉得复数 “不正常”。我们要保持开放的心态：未来的人们可能会觉得，直到 21 世纪初还有人不信任复数，是件很可笑的事。

Carl Gauss, the famous mathematician, wrote:
著名数学家卡尔・高斯曾写道：

“Hätte man +1, -1, √-1 nicht positiv, negative, imaginäre (oder gar ummögliche) Einheit, sondern etwa directe, inverse, laterale Einheit genannt, so hätte von einer solchen Dunklelheit kaum die Rede sein können.”

“If +1, -1, √-1 had not been called a positive, negative, imaginary (or even impossible) unit, but rather a direct, inverse, lateral unit, then there could hardly have been any talk of such obscurity.”
“如果人们没有把 +1, -1, √-1 称为正单位、负单位、虚单位（甚至不可能单位），而是称为正向单位、反向单位、侧向单位，那么就不会有那么多关于‘晦涩难懂’的讨论了。”

If you want more nitty-gritty, check out wikipedia, the Dr. Math discussion, or another argument on why imaginary numbers exist...
如果你想了解更多细节，可以看看维基百科、数学博士论坛的讨论。

---

Understanding Why Complex Multiplication Works

理解复数乘法的原理

Viewing imaginary numbers as rotations is one of the most insightful realizations:
将虚数理解为旋转，是最具启发意义的认知之一：

$i$, the square root of $-1$, is a number belonging to a different dimension. Once this concept is understood, multiplication can be used to “combine” the rotations of two complex numbers:
$i$（即 $-1$ 的平方根）是属于不同维度的数。一旦理解这一概念，便可通过乘法“结合”两个复数的旋转效果：

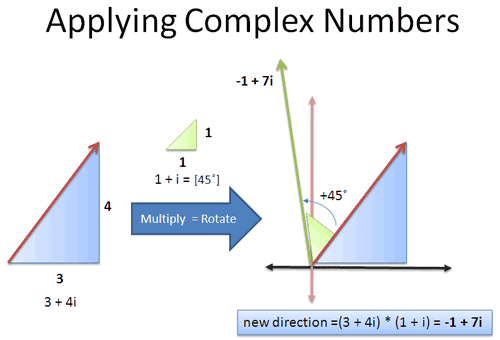
This finding is highly illuminating: angles can be added without using sine or cosine functions. Unfortunately, there was no intuitive understanding of why this phenomenon occurs. The following content will address this question.
这一发现极具启发意义：无需使用正弦或余弦函数即可实现角度相加。但遗憾的是，此前尚未形成对该现象背后原理的直观理解，下文将对此展开分析。

The Boring Explanation: How?

常规解释：实现过程

The common explanation for why complex multiplication leads to angle addition is as follows. First, express complex numbers in polar coordinates (radius and angle):
关于复数乘法为何会导致角度相加，常规解释如下。首先，将复数表示为极坐标形式（模长与角度）：

$r_1(\cos (a)+i\sin (a))\cdot r_2(\cos (b)+i\sin (b))$

Next, calculate the product and group the terms by real and imaginary parts:
接着，计算乘积并按实部与虚部分组：

$$\begin{gathered} =(r_1\cos (a)\cdot r_2\cos (b)-r_1\sin (a)\cdot r_2\sin (b))+i(r_1\cos (a)\cdot r_2\sin (b)+r_2\cos (b)\cdot r_1\sin (a)) \\ =r_1\cdot r_2[(\cos (a)\cdot \cos (b)-\sin (a)\cdot \sin (b))+i(\cos (a)\cdot \sin (b)+\cos (b)\cdot \sin (a))] \end{gathered}$$

Finally, it can be observed that the above expression matches the sine and cosine angle addition formulas:
最后可发现，上述表达式与正弦、余弦的角加法公式完全一致：

$$\begin{gathered} \cos (a+b)=\cos (a)\cdot \cos (b)-\sin (a)\cdot \sin (b) \\ \sin (a+b)=\cos (a)\cdot \sin (b)+\cos (b)\cdot \sin (a) \end{gathered}$$

This completes the derivation. If you cannot intuitively understand the expansion of sine and cosine functions, it is worth noting that the mathematical reasoning is logically consistent.
至此推导完成。若无法直观理解正弦与余弦函数的展开过程，需明确该数学推理在逻辑上是严谨成立的。

…

If you are still reading, that is excellent. The problem with this explanation is that it lacks intuitiveness: it is analogous to stating two poems are similar based on the analysis of letter distribution—accurate but unsatisfying.
若您仍在阅读，非常好。该解释的问题在于缺乏直观性：其类似于通过字母分布分析得出两首诗相似的结论，虽准确但无法带来认知上的满足感。

Sine functions are valuable, but detailed analysis should be conducted only after understanding the key relationship.
正弦函数具有重要意义，但对其细节的分析应在理解关键关联后进行。

The Fun Explanation: Why!

有趣的解释：为什么！

To restate the key question: why does multiplying two complex numbers result in the addition of their angles?
重申关键问题：为何两个复数相乘会导致其角度相加？

First, clarify the effect of multiplication:
首先，明确乘法的作用：

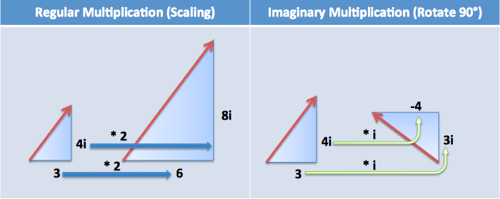
• Regular multiplication (e.g., “multiply by $2$”) scales a number (increasing or decreasing its magnitude).
  普通乘法（如“乘以 $2$”）对数字进行缩放（增大或减小其模长）。

• Imaginary multiplication (e.g., “multiply by $i$”) rotates a number by $90$ degrees.
  虚数乘法（如“乘以 $i$”）使数字旋转 $90$ 度。

What happens when these two effects are combined in a complex number? Multiplying by $(2+i)$ means “scale the number by a factor of $2$, and then apply a perpendicular rotation”.
当这两种效果在复数中结合时，结果如何？乘以 $(2+i)$ 意味着“将数字缩放 $2$ 倍，再施加一个垂直方向的旋转”。

A simple example:
简单示例：
$4\cdot (3+i)=4\cdot 3+4\cdot i=12+4i$

Specifically, take the original number $(4)$, scale it by a factor of $3$ ($4\times 3$), and then apply the rotation effect ($+4i$). To achieve only rotation, multiply by $i$; to achieve only scaling, multiply by a real number such as $3$. A complex number $(a+bi)$ integrates both effects.
具体而言，取原始数字 $(4)$，将其缩放 $3$ 倍（$4\times 3$），再施加旋转效果（$+4i$）。若仅需旋转，可乘以 $i$；若仅需缩放，可乘以 $3$ 等实数。复数 $(a+bi)$ 则集成了这两种效果。

Visualizing Complex Multiplication

复数乘法的可视化表达

The above example, involving a real number $(4)$ multiplied by a complex number $(3+i)$, is straightforward. What about multiplying two complex numbers (represented as “triangles”), such as $(3+4i)\cdot (2+3i)$?
上述“实数 $(4)$ 与复数 $(3+i)$ 相乘”的示例较为简单。若两个乘数均为复数（表现为“三角形”），如 $(3+4i)\cdot (2+3i)$，结果又如何？

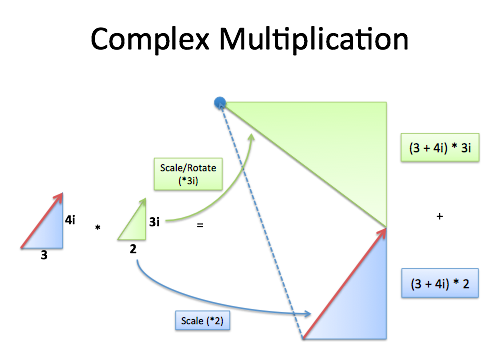
This scenario is more representative. It can be understood as: “Create a scaled version of the original triangle (scaled by a factor of $2$), and add a scaled and rotated triangle (scaled by a factor of $3$ and rotated via $i$)”. The final endpoint corresponds to the new complex number.
该场景更具代表性，可理解为：“生成原始三角形的缩放版本（缩放 $2$ 倍），再叠加一个经过缩放与旋转的三角形（缩放 $3$ 倍且通过 $i$ 实现旋转）”。最终的端点即为新复数对应的坐标。

Alternative explanations are also valuable, and here is another perspective:
多种解释视角具有参考价值，以下为另一种理解方式：

Instead of grouping the multiplication by triangles, analyze each term according to the FOIL rule (First, Outside, Inside, Last). Summing these terms is equivalent to moving along a specific path, which ultimately leads to the same endpoint.
不再以三角形为单位对乘法进行分组，而是依据 FOIL 法则（首项、外项、内项、末项）分析每一项。对这些项求和，相当于沿特定路径移动，最终会到达同一端点。

But What About the Angles?

角度的关联性分析

The key question remains: although it appears that angles are added, how to confirm this conclusion?
关键问题仍需明确：尽管从表象看角度在相加，但如何验证这一结论？

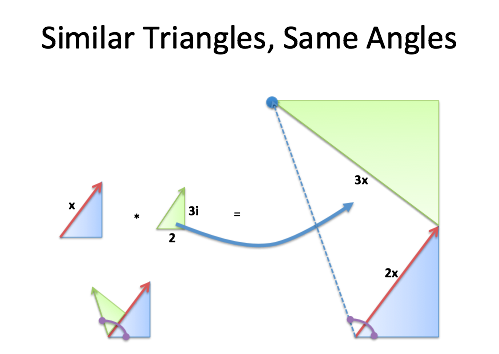
Geometric principles provide a solution. As recalled from ninth-grade geometry knowledge, does the angle of the result (represented by the dotted blue line) match the angle obtained by superimposing the two triangles?
几何原理可为此提供解答。结合九年级几何知识可知，结果（蓝色虚线所示）的角度，是否与将两个三角形叠加后得到的角度一致？

In the standard case, start with the triangle corresponding to $(3+4i)$, then superimpose the triangle corresponding to $(2+3i)$ to obtain the combined angle.
在标准场景中，先取 $(3+4i)$ 对应的三角形，再叠加 $(2+3i)$ 对应的三角形，即可得到合角度。

In the multiplication process, start with a scaled triangle (scaled by a factor of $2$), then superimpose another scaled triangle (scaled by a factor of $3$ and rotated via $i$). Although the triangles are larger, similar triangles have identical angles—only their magnitudes differ.
在乘法运算中，先取缩放后的三角形（缩放 $2$ 倍），再叠加另一个缩放后的三角形（缩放 $3$ 倍且通过 $i$ 旋转）。尽管三角形尺寸增大，但相似三角形的角度完全相同，仅模长存在差异。

Scaling the original triangle does not change its angle; superimposing another scaled triangle also does not change the angle. Therefore, the final angle remains consistent. This process—scaling, rotating, and obtaining the combined angle—is intuitive. Importantly, this is not a property unique to “imaginary numbers” but a method for combining triangles without trigonometric functions.
对原始三角形进行缩放不会改变其角度，叠加另一个缩放后的三角形同样不会改变角度，因此最终角度保持一致。这一“缩放—旋转—得到合角度”的过程具有直观性，且并非“虚数”的特有属性，而是一种无需三角函数即可组合三角形的方法。

Side Effects May Include Scaling

缩放效应的附带分析

It is noteworthy that the process involves creating enlarged copies of the original triangle and summing them. How does the magnitude change compared to the initial blue triangle?
需注意的是，该过程涉及生成原始三角形的放大版本并对其求和。与初始蓝色三角形相比，模长的变化规律是什么？

Let the original length be $x$. Regardless of the value of $x$, the final superimposed new triangle has a magnitude of $2x+3x$ (with the general form $ax+bx$). According to the Pythagorean theorem, the “actual” distance is calculated as follows:
设原始长度为 $x$。无论 $x$ 取值如何，最终叠加的新三角形模长为 $2x+3x$（一般形式为 $ax+bx$）。根据勾股定理，“实际”距离的计算公式为：

$\sqrt{(ax{)}^2+(bx{)}^2}=\sqrt{x^2(a^2+b^2)}=x\cdot \sqrt{a^2+b^2}$

Specifically, the original distance ($x$) is scaled by the magnitude of the new triangle (i.e., the magnitude of $a+bi$).
具体而言，原始距离（$x$）需乘以新三角形的模长（即 $a+bi$ 的模长），得到新距离。

If the magnitude of the new triangle is $1$ (i.e., $a^2+b^2=1$), the distance remains unchanged.
若新三角形的模长为 $1$（即 $a^2+b^2=1$），则距离保持不变。

A Few Thoughts

若干思考

Rigorous proofs are not inherently undesirable; the issue arises when they are presented as helpful when they are not. Proofs serve two purposes:
严谨的证明本身并非不可取，问题在于当证明无实际帮助时，仍被当作有效工具。证明具有两个目的：

• To demonstrate that a result is true. This is primarily for mathematicians presenting research findings—students rarely question the validity of mathematical facts in classroom settings.
  证明某一结果“是否正确”。这主要面向呈现研究成果的数学家，学生在课堂场景中极少质疑数学事实的有效性。
• To explain why a result is true.
  解释某一结果“为何正确”。

Authentic and satisfying insights stem from analyzing analogies and examples, rather than reading condensed, minimalist proofs—especially those that rely on sine or cosine addition formulas.
真正且令人满意的洞见，源于对类比与示例的分析，而非阅读精简的极简证明（尤其是依赖正弦或余弦加法公式的证明）。

Polya put it well: “When you have satisfied yourself that the theorem is true, you start proving it."
波利亚曾有精辟论述：“当你确信定理正确后，再着手证明它。”

Happy learning of mathematics.
祝您数学学习顺利。

---

via:

• 虚数的意义 - 阮一峰的网络日志 阮一峰 2012 年 9 月 24 日
  https://ruanyifeng.com/blog/2012/09/imaginary_number.html
• definition - What are imaginary numbers?
  https://math.stackexchange.com/questions/199676/what-are-imaginary-numbers
• A Visual, Intuitive Guide to Imaginary Numbers
  https://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/
• Understanding Why Complex Multiplication Works – BetterExplained
  https://betterexplained.com/articles/understanding-why-complex-multiplication-works/
• Imaginary Number – BetterExplained
  https://betterexplained.com/topics/imaginary-number/