1. backgroud
小样本是个工业界是个广泛存在的问题,领域内相关研究也非常多,不过众多研究未必都可以经受住业务的考验,本文主要结合工作业务探索一下相关技术的收益情况, 所选择的任务为文本分类,模型采用Roberta。
2.method
2.1 数据增强- embedding层面
2.1.1 mixup
mixup技术最初来源于CV领域,它的思路其实很简单:针对两个训练样本( x i , y i x^{i}, y^{i} xi,yi)和( x j , y j x^{j}, y^{j} xj,yj),可以以一定的 λ ∈ B e t a \lambda \in Beta λ∈Beta因子来对这两个样本进行线性插值来得到一条增强样本:
x ^ i , j = λ ∗ x i + ( 1 − λ ) ∗ x j y ^ i , j = λ ∗ y i + ( 1 − λ ) ∗ y j \hat x^{i,j}=\lambda * x^{i}+(1-\lambda)*x^{j}\\\hat y^{i,j}=\lambda*y^{i}+(1-\lambda)*y^{j} x^i,j=λ∗xi+(1−λ)∗xjy^i,j=λ∗yi+(1−λ)∗yj
从公式可以看出,增强样本不仅数据分布做了交叉,标签也进行了交叉,约束模型学习到的结果其实是个线性值,通过更多的增强样本,其实就约束了模型对噪音数据的拟合,从而起到正则化的效果。
不过由于nlp数据天然不同于cv数据,所以这一种方法也无法直接应用于nlp领域,因为nlp的token不像cv一样规整,可以直接插值处理,所以开始的很多研究就是聚焦于在隐层(包括hidden层及embedding层)来做插值运算,比较有代表性的技术就是word mixup以及sentence mixup:


本⽂采⽤的是2013年Simonyan结合2016年Li等提出的基于梯度(Gradient-based)的⽅法,这⾥就是通过计算input的embedding(e)的导数来表示该token的重要程度s(saliency scores),然后统计 x B x^{B} xB固定窗口大小内的段对应的最终选择得分并从中选择最大得分的段 s e g m e n t B segment^{B} segmentB,根据同样的方法从 x A x^{A} xA中选择最小得分的段 s e g m e n t A segment^{A} segmentA, 保证两段等长,然后用 s e g m e n t B segment^{B} segmentB去替换 s e g m e n t A segment^{A} segmentA








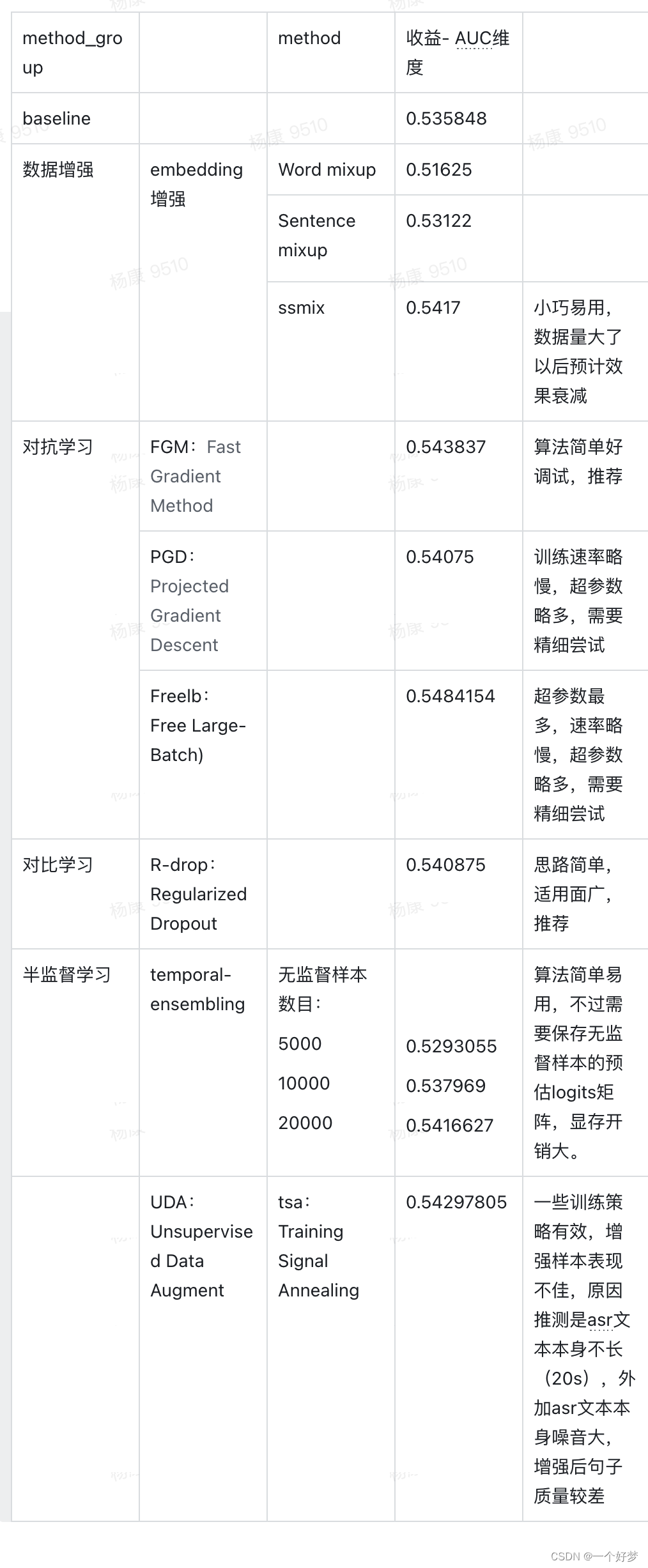
 本文探讨了自然语言处理中的小样本问题,重点介绍了数据增强和半监督学习方法。在数据增强方面,讨论了embedding层面的mixup、对抗训练(FGM、PGD、FreeLB)以及对比学习。在半监督学习中,提到了Temporal Ensembling、Mean Teachers和UDA(Unsupervised Data Augmentation)算法,强调了无监督学习在模型泛化能力提升中的作用。
本文探讨了自然语言处理中的小样本问题,重点介绍了数据增强和半监督学习方法。在数据增强方面,讨论了embedding层面的mixup、对抗训练(FGM、PGD、FreeLB)以及对比学习。在半监督学习中,提到了Temporal Ensembling、Mean Teachers和UDA(Unsupervised Data Augmentation)算法,强调了无监督学习在模型泛化能力提升中的作用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 842
842

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








