洛谷 U411986 数的范围（二分模板）

题意：在一个有序序列里面找某个值的初始出现下标和最后出现下标，如果该值不存在，输出-1 -1。

整数二分模板题，该题主要用来练习如何写两种情况下的二分函数的代码模板。

1）upper_bound函数：用来寻找边界点A，即是在区间[0, A]中，所有元素都满足同一个性质的最右边界。

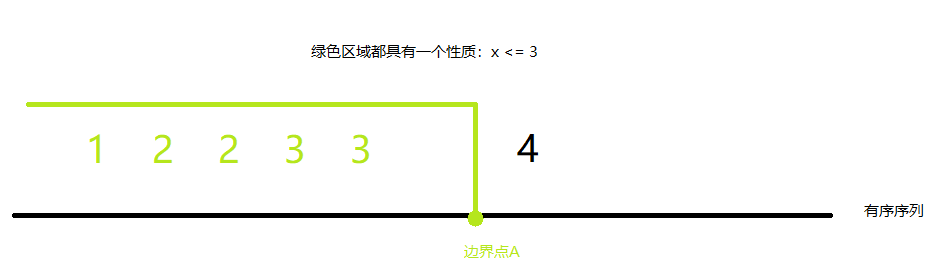
如果我们把区间通过中间点mid=(l+r)/2来划分成两个长度一样的子区间，则下标为mid的值array[mid]计算出来的性质可能会有这两种情况：

a）值array[mid]满足绿色区间性质：

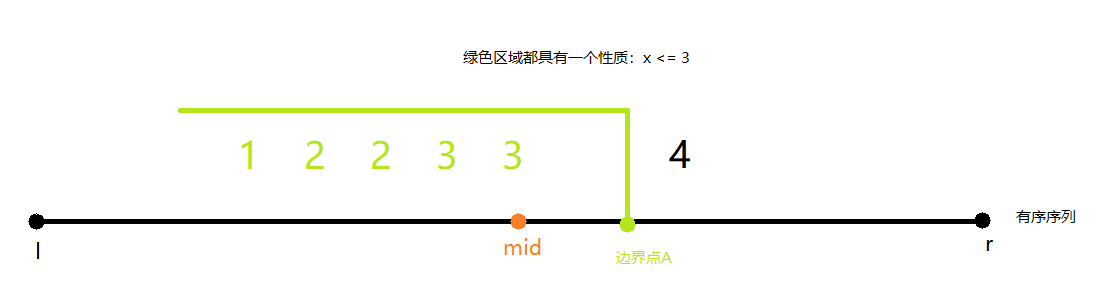
那么由图可以看出，边界点A的位置，一定在右半边子区间，极端情况下，mid有可能就是边界点A。所以下一个我们要去搜索的区间范围可以缩减为：

[mid,r]，l更新为mid。

注意这里mid是包含的。

b）值array[mid]不满足绿色区间性质：

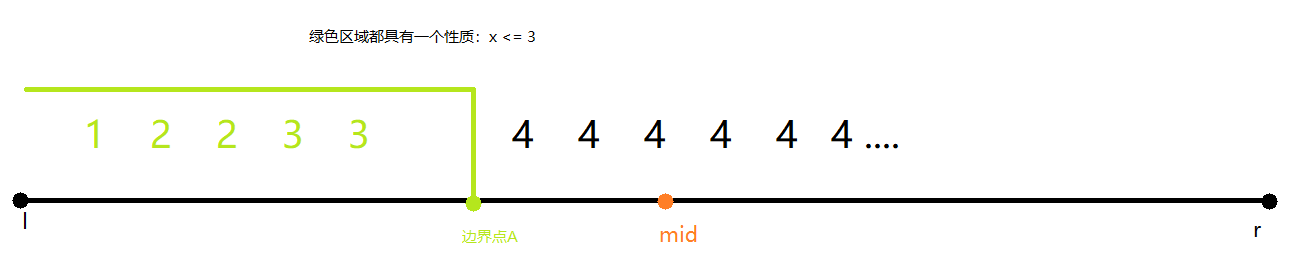
那么由图可以看出，边界点A的位置，一定在左半边子区间，而且mid不可能是边界点A。

所以下一个我们要去搜索的区间范围可以缩减为：

[l,mid-1]，r更新为mid-1。

搜索终止的条件是l和r相等，且边界点A的解为l或者r。

代码模板如下：

int find_a(int k) {
    int l = 0, r = n-1;
    while (l < r) {
        int mid = (l + r + 1) / 2;
        if (arr[mid] <= k)
            l = mid;
        else
            r = mid -1;
    }
    return l;
}

这里注意到模板中mid的取值是(l+r+1)/2，而不是(l+r)/2，是因为mid的取值是向下取整的，当l和r只相差1时，mid=(l+r)/2就等于(2*l+1)/2=l，如果此时需要更新的是区间左端点l，那么l=mid操作一通后，l的值还是原来的值，会导致死循环。

所以把mid的值设置为(l+r+1)/2，这样分区间时还是可以视为是对半分的，还可以避免死循环。

1）lower_bound函数：用来寻找边界点B，即是在区间[B, n-1]中，所有元素都满足同一个性质的最左边界。

我们用同样的方法分析两种mid存在的情况：

a）值array[mid]满足红色区间性质：

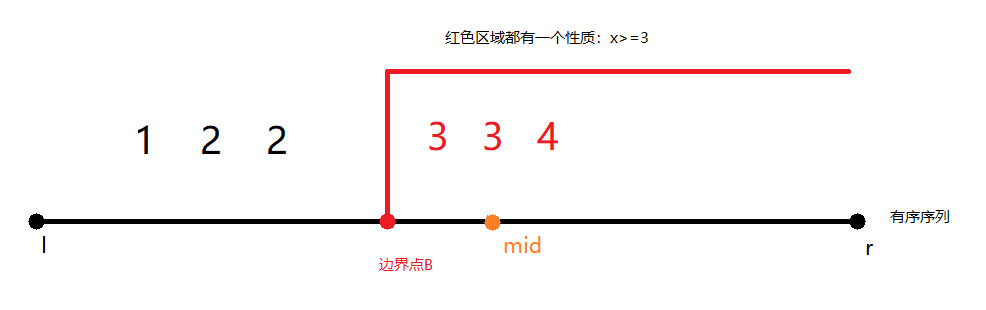
那么更新的下一个搜索区间为：[l，mid]。

b）值array[mid]不满足红色区间性质：

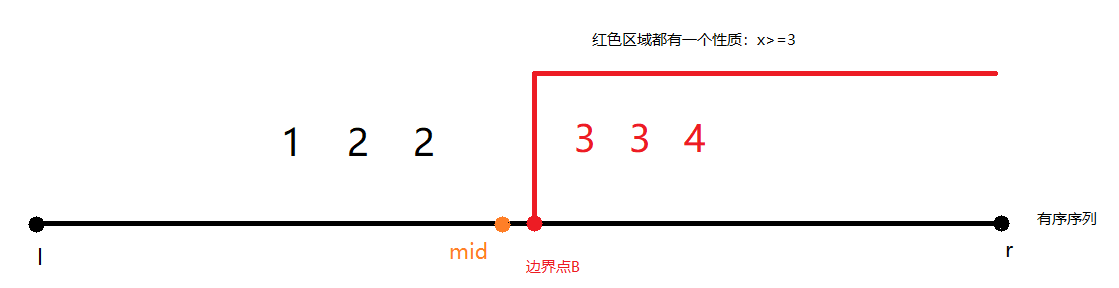
那么更新的下一个搜索区间为：[mid+1,r]。

代码模板如下：

int find_b(int k) {
	int l = 0, r = n-1;
	while (l < r) {
		int mid = (l + r) / 2;
		if (arr[mid] >= k)
			r = mid;
		else
			l = mid + 1;
	}
	// 找到的边界B的值就是l，也是r，因为l==r 
	return l;
}

本题AC代码如下：

#include<iostream>
#include<algorithm>
using namespace std;

const int MAXN = 100010;
int arr[MAXN];
int n, q;

int find_b(int k) {
	int l = 0, r = n-1;
	while (l < r) {
		int mid = (l + r) / 2;
		if (arr[mid] >= k)
			r = mid;
		else
			l = mid + 1;
	}
	// 找到的边界B的值就是l，也是r，因为l==r 
	if (arr[l] == k)
		return l;
	return -1;
}

int find_a(int k) {
	int l = 0, r = n-1;
	while (l < r) {
		int mid = (l + r + 1) / 2;
		if (arr[mid] <= k)
			l = mid;
		else
			r = mid -1;
	}
	return l;
}

int main() {
	while (~scanf("%d%d", &n, &q)) {
		for (int i=0; i < n; i++)
			scanf("%d", arr+i);
		while (q--) {
			int k;
			scanf("%d", &k);
			int start = find_b(k), end;
			if (start == -1) {
				printf("-1 -1\n");
			} else {
				end = find_a(k);
				printf("%d %d\n", start, end);
			}
		}
	}
	return 0;
}