假设 特征 和 结果 都满足线性。即不大于一次方。这个是针对 收集的数据而言。
收集的数据中,每一个分量,就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数,向量表示形式:
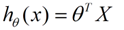
这个就是一个组合问题,已知一些数据,如何求里面的未知参数,给出一个最优解。 一个线性矩阵方程,直接求解,很可能无法直接求解。有唯一解的数据集,微乎其微。
基本上都是解不存在的超定方程组。因此,需要退一步,将参数求解问题,转化为求最小误差问题,求出一个最接近的解,这就是一个松弛求解。
求一个最接近解,直观上,就能想到,误差最小的表达形式。仍然是一个含未知参数的线性模型,一堆观测数据,其模型与数据的误差最小的形式,模型与数据差的平方和最小:
这就是损失函










 线性回归用于处理特征与结果呈线性关系的数据。由于实际数据往往是超定方程组,直接求解参数不可行,因此采用最小误差的松弛求解策略。损失函数以模型与数据差的平方和最小为目标,通过最小二乘法或梯度下降法(如批梯度下降、增量梯度下降)进行优化。最小二乘法要求X是列满秩的,而梯度下降法关注偏导数、学习率和收敛性。
线性回归用于处理特征与结果呈线性关系的数据。由于实际数据往往是超定方程组,直接求解参数不可行,因此采用最小误差的松弛求解策略。损失函数以模型与数据差的平方和最小为目标,通过最小二乘法或梯度下降法(如批梯度下降、增量梯度下降)进行优化。最小二乘法要求X是列满秩的,而梯度下降法关注偏导数、学习率和收敛性。
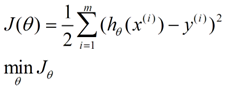

 订阅专栏 解锁全文
订阅专栏 解锁全文

















 1113
1113

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










