吴恩达机器学习——第16章 异常检测

1、定义

异常检测算法用来判断一个样本是否属于异常值。
此处的异常值指的是不同于大多数样本的值。

比如一个制造发动机引擎的公司，有很多很多引擎样本，这些样本都是类似的，如果发现某个样本离这些样本很远，则这个样本是异常样本的概率就很大。

如上图所示，根据样本建立了一个模型，模型中心代表样本是正常的，离中心越远则异常的概率越大，绿色标识的样本离模型中心很远则为异常样本。

2、基本原理

异常检测基于高斯分布实现，下面回顾一下高斯分布的知识点。

2.1 高斯分布

高斯分布，也叫正态分布，公式为:
$$P(X;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(X-\mu {)}^2}{2{\sigma }^2})$$
下面解释下各个项的含义：

• P：代表的是概率，$P(X;\mu ,{\sigma }^2)$的含义是X在$\mu ,{\sigma }^2$的影响下的概率。
• 当样本满足高斯分布时，我们这么表示：X~$P(\mu ,{\sigma }^2)$
• $\mu$：代表高斯分布的中心位置。
• $\sigma$：标准差，代表钟形的宽度。

2.1.1 参数对图形的影响

由上图可以看出，$\mu$影响的是图形中心的位置，而$\sigma$影响的是图形的平滑度，$\sigma$越大，则坡度越小。

2.1.2 参数的计算

下面根据样本计算出 $\mu$ 和 $\sigma$ 的值。

$\mu =\frac{1}{m}{\sum }_{i=1}^m{X}^{(i)}$

${\sigma }^2=\frac{1}{m}{\sum }_{i=1}^m(X^{(i)}-\mu {)}^2$

2.2 算法

$$P(X;\mu ,{\sigma }^2)=P(x_1;\mu ,{\sigma }^2)P(x_2;\mu ,{\sigma }^2)P(x_3;\mu ,{\sigma }^2)......P(x_n;\mu ,{\sigma }^2)$$
累乘可以简写为：$={\prod }_{j=1}^{n}P(x_j;{\mu }_j,{\sigma }_j^2)$

2.3 计算过程

异常检测算法的执行步骤是：

• 收集数据集。
• 计算$\mu ,{\sigma }^2$。
• 代入公式，计算每个样本的概率。当概率大于某个阈值时，表示样本为正样本，否则为负样本，阈值使用$ϵ$表示。

2.4 评估方式

异常检测算法属于无监督学习算法，无法根据Y值评估模型的好坏，也无法一次性给出一个合适的比较阈值$ϵ$，下面看看如何解决这些问题。

• 选择正样本作为训练集。
• 选择正样本和异常样本作为交叉验证集和测试集。
• 在正样本上训练模型P(X)。
• 在交叉训练集上进行验证，使用不同的阈值$ϵ$进行测试，根据F1值或者查准率、查全率的比率来选择$ϵ$。
• 在测试集上进行测试，计算F1值或者查准率、查全率。

3、异常检测VS监督学习

下面对异常检测算法和监督学习的适用场景进行对比。

• 异常检测：适用于正常样本、异常样本的比率失调的情况，比如说正样本占的比率非常大或非常小的情况。比率大的一方用来训练模型。例如欺诈行为、生产飞机引擎等。
• 监督学习：适用于正常样本、异常样本的比率相当的情况。比如邮件过滤、天气预报等。

4、设计特征

首先，在异常检测问题中，特征需要符合高斯分布，可以通过求对数、小数次方等方式对特征进行二次处理。

其次，有一些异常样本拥有非常高的P(X)，这时候通过当前的特征进行计算就不足了，需要重新进行分析，发现新的特征或组合特征帮助我们进行计算。

5、 多元高斯分布

上面介绍的高斯分布中，如果有多个特征的情况下，是通过累乘的方式叠加的，但是当两个特征的相关性比较强时，一般高斯分布就不能适应了。

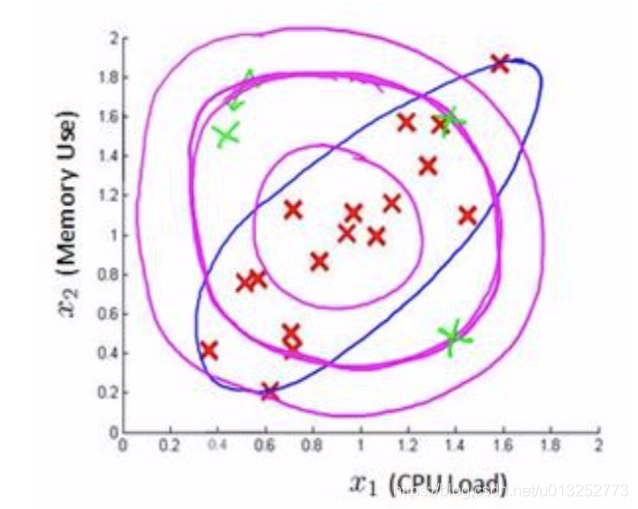
如上图所示，x1 x2是两个特征，洋红色的圈是一般高斯分布，可以看到绿色的异常点在模型中的比率是比较高的，也就是不能把异常点区分出来。

而蓝色的圈就是多元高斯分布的图形，可以看到它很好的把异常点排除在外了。

5.1 算法

多元高斯分布与一般高斯分布的区别在于，多元高斯分布将建立特征的协方差矩阵，然后对特征同时建模，而一般高斯分布是分别建模然后累乘。

$\mu$的计算公式不变：$\mu =\frac{1}{m}{\sum }_{i=1}^m{X}^{(i)}$

协方差矩阵$\Sigma =\frac{1}{m}{\sum }_{i=1}^m(x^{(i)}-\mu )(x^{(i)}-\mu {)}^T=\frac{1}{m}(X-\mu {)}^T(X-\mu )$

多元高斯分布的公式为：
$$P(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$

参数的含义：

• $|\Sigma |$：代表行列式，Octave中使用$det(\Sigma )$计算。
• ${\Sigma }^{-1}$：代表逆矩阵
• $||\Sigma ||$：代表？

5.2 参数的影响

协方差矩阵的正对角线，影响的是特征的偏差；反对角线影响的是特征的关联性，正数代表正关联，负数代表负关联性。

如上图所示，依次分析：

• 一般高斯分布，特征的偏差都是一致的。
• 通过协方差矩阵，令x1拥有较小的偏差。
• 通过协方差矩阵，令x2拥有较大的偏差。
• 通过协方差矩阵，增加两个特征的正相关性。
• 通过协方差矩阵，增加两个特征的负相关性。

5.3 对比

一般高斯分布:

• 不能表达两个特征之间的关联关系，但是可以通过增加新特征的方式来建立关系。
• 计算速度快。
• 能支撑很大的特征量。

多元高斯分布:

• 能自然支撑多特征间的关联关系。
• 计算量大，支撑的特征量有限。
• 假设样本的数量m，特征数量为n，则需要满足m>10*n，否则会造成协方差矩阵不可逆的问题。

多元高斯算法中，除了m<10*n造成协方差矩阵不可逆之外，多个特征相等或有线性关系，也会造成协方差矩阵不可逆的问题。

参考资料

协方差矩阵参考降维中的3.1章：降维

F1？

查准率、查全率？