[深度学习] 梯度消失与梯度爆炸、Loss为Nan的原因

现象

如何确定是否出现梯度爆炸？

在训练过程中出现梯度爆炸会伴随一些细微的信号，如：

（1）模型无法从训练数据中获得更新；

（2）模型不稳定，导致更新过程中的损失出现显著变化；

（3）训练过程中，模型的损失变为Nan。

 

梯度消失与梯度爆炸原因

首先，来看神经网络更新梯度的原理，即反向传播算法。

详细推导参考：反向传播算法

通过反向传播算法更新梯度的公式可以看到，影响梯度更新的有，初始权重、激活函数、梯度流动方式、损失值过大等。

下面分别来一一进行介绍：

（1）初始权重带来的影响：神经网络权重初始化不当；

（2）激活函数带来的影响：激活函数选择不当；

（3）梯度流动方式带来的影响：网络结构本身的问题，如RNN；

（4）损失值过大带来的影响：数据集的问题，如标注不准等。

下面，就来对这几种情况分别进行一一介绍。

 

神经网络权重初始化不当

深度神经网络训练的时候，采用反向传导的方式，其背后的本质是链式求导，计算每层梯度的时候会涉及到一些连乘操作。每一层的残差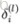都由后一层的残差乘以两层之间的权重矩阵，再乘以当前层的激活函数的导数得到。因此，神经网络权重的初始化至关重要，不当的初始化可能会带来梯度消失或者梯度爆炸。

当网络过深，如果连乘的因子大部分小于1，最后乘积可能趋于0；另一方面，如果连乘的因子大部分大于1，最后乘积可能趋于无穷。这就是所谓的梯度消失与梯度爆炸。

防止因权重初始化不当带来的梯度爆炸：

(1) 使用Xavier初始化法或者MSRA初始化法，使得在深度网络的每一层，激活值都有很好的分布。

(2) 使用预训练模型，初始化已有网络层的权重。

 

激活函数选择不当

神经网络常用的激活函数可参考：[深度学习] 神经网络的激活函数

sigmoid函数：

tanh函数：

 

如果选择sigmoid 或者 tanh 函数，由它们的曲线可以看出，当输入很大或者很小的时候，饱和的神经元会带来梯度消失。

防止因激活函数选择不当带来的梯度消失：

1.最常使用Relu，需要小心地调节学习速率（如果relu参数初始化不理想，前向计算结果为负值，则进行梯度计算的时候全部变为0，在反向计算的时候也会没有响应）；

2.偶尔可考虑Relu的变种，如Leaky Relu；

3.一般不使用sigmoid

 

神经网络本身的结构问题，如RNN

RNN相当于把许多循环神经网络单元连接成一个序列。可以设想梯度流穿过，当我们要计算关于h0的损失函数的梯度时，反向传播需要经过RNN中的每一个单元。每次反向传播经过一个单元时，都要使用其中某一个W的转置。

这意味着最终的表达式对h0梯度的表达式将会包含很多很多权重矩阵因子，这样不断对同一个值做乘法，是非常糟糕的。

在标量情况下，要么当这个值的绝对值大于1时，发生梯度爆炸；要么当这个值的绝对值小于1时，发生梯度消失，直到为0。既不发生梯度爆炸也不发生梯度消失，也就是当这个值正好为1。

对于矩阵而言，需要关注矩阵的最大奇异值，如果最大奇异值大于1，会发生梯度爆炸；如果最大奇异值小于1，会发生梯度消失。

防止因使用循环神经网络RNN带来的梯度消失与梯度爆炸问题：

1.设置梯度剪切阈值（gradient clipping threshold），一旦梯度超过该值，直接设置为该值；

2.使用沿时间的截断反向传导方法（详见[深度学习]循环神经网络：RNN，LSTM，GRU，Attention机制，沿时间的截断反向传导算法）；

2.使用更加复杂的RNN结构，例如LSTM。

LSTM能尽量避免梯度爆炸或者梯度消失的原因有两个：

1.这里的遗忘门是矩阵元素相乘，而不是矩阵相乘。

2.矩阵元素相乘，可能会在不同的时间点乘以一个不同的遗忘门。

3.遗忘门是一个sigmoid函数，所以矩阵元素相乘的结果，会保证在(0,1)之间。

4.从最后的隐藏单元状态，反向传播到第一个单元状态，在反向传播的路径上，我们只通过一个单一的非线性tanh向后传播，而不是在每一个时间步长中单独设置tanh函数。

 

数据集本身问题

数据集本身可能标注不准确，引入大量噪声。以图片数据集为例，具体情况可能包括：

1.在目标检测中，四边形标注框与实际不匹配，标注框的面积过多大于实际目标的面积；

2.在使用mask rcnn检测目标时，只用四点标注的bounding boxes来生成mask，可能会导致生成的mask不够准确。如果偏差过大，也会引入梯度爆炸；

3.在场景文字检测中，为了套用已有的检测水平方向物体的目标检测框架，将原有的任意四边形标注框转换为其水平方向的最小外接矩形，也会导致标注框的面积过多大于实际目标的面积；

4.在场景文字识别中，对于一张完整的图片，一般是根据坐标对单词区域进行裁剪，再将所有的单词区域缩放成相同的大小。一是单词区域裁剪不准确，二是如果缩放尺寸没有选择好，较小的图片放大成过大的尺寸，会使得训练图片非常模糊，引入大量噪声。

对于数据集本身的问题，带来的梯度爆炸问题，一般需要注意，尽量使得标注准确，除非是进行难样本挖掘操作，一般尽量使用清晰的图片。

 

loss为Nan原因

1.梯度爆炸。梯度变得非常大，使得学习过程难以继续。

2.不当的损失函数。

3.不当的输入。

4.池化层中步长比卷积核的尺寸大。